Поиск на графе

Функции АТД поиска на графе

Поиск в глубину и другие методы поиска на графах, которые будут рассмотрены ниже в этой главе, выполняют переходы по ребрам графа от одной вершины к другой, чтобы систематически обойти все вершины и все ребра графа. Однако переход от вершины к вершине по ребрам может привести только ко всем вершинам того связного компонента, которому принадлежит исходная вершина. Конечно, в общем случае графы могут быть и не связными, и тогда придется вызывать функцию поиска для каждого связного компонента. Обычно мы будем использовать функции поиска на графе, которые выполняют следующие действия, пока все вершины графа не будут помечены как посещенные:

• Найти непомеченную вершину (начальная вершина).
• Посетить (и пометить как посещенные) все вершины в связном компоненте, который содержит начальную вершину.

Способ маркировки в этом описании не задан, но в большинстве случаев применяется тот же метод, что и для реализаций DFS в разделе 18.2: вначале мы заносим во все элементы приватного вектора, индексированного именами вершин, отрицательные целые числа, а затем помечаем вершины, присваивая соответствующим компонентам вектора неотрицательные значения. Вообще-то для этого достаточно устанавливать значение всего лишь одного (знакового) разряда, но большинство реализаций хранит в векторе и другую информацию, имеющую отношение к помеченным вершинам (например, в реализации DFS из раздела 18.2 это порядок, в котором помечаются вершины). Не определен и способ поиска вершин в следующем связном компоненте, но чаще всего применяется просмотр этого вектора в порядке возрастания индекса.

Мы передаем в функцию поиска ребро (используя фиктивную петлю в первом вызове для каждого связного компонента), а не концевую вершину назначения, т.к. ребро указывает, как выйти в эту вершину. Знание ребра равносильно знанию, какой коридор привел к конкретному перекрестку в лабиринте. Эта информация полезна во многих классах DFS. Если мы просто отслеживаем посещения вершин, то от этой информации мало толку, поскольку для решения более интересных задач необходимо знать, откуда мы пришли.

Реализация в программе 18.2 демонстрирует все эти возможности. На рис. 18.8 показано влияние процесса посещения всех вершин на вектор ord любого производного класса. Как правило, производные классы, которые мы будем рассматривать, исследуют и все ребра, инцидентные каждой посещенной вершине. В таких случаях знание, что мы посетили все вершины, говорит, что мы посетили и все ребра, как в методе Тремо.

Программа 18.2. Поиск на графе

Данный базовый класс предназначен для обработки графов, которые могут быть несвязными. Производные классы должны содержать определение функции searchC, которая, будучи вызванной с петлей вершины v в качестве второго аргумента, заносит в ord[t] значение cnt++ для каждой вершины t, содержащейся в том же связном компоненте, что и v. Обычно конструкторы в производных классах вызывают функцию search, которая, в свою очередь, вызывает searchC для каждого связного компонента графа.

  template <class Graph>
  class SEARCH
    { protected: const Graph &G;
      int cnt;
      vector <int> ord;
      virtual void searchC(Edge) = 0;
      void search()
        { for (int v = 0; v < G.V(); v++)
          if (ord[v] == -1) searchC(Edge(v, v));
        }
    public:
      SEARCH (const Graph &G) : G(G),
        ord(G.V(), -1), cnt(0) { }
      int operator[](int v)
        const { return ord[v]; }
    };
      

Рис. 18.8. Поиск на графе

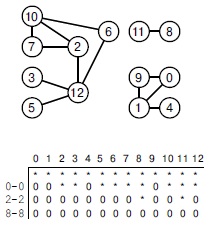
Таблица в нижней части рисунка содержит метки вершин (содержимое вектора ord) во время обычного поиска на графе, приведенном в верхней части рисунка. Сначала функция GRAPHsearch из программы 18.2 снимает пометки со всех вершин, т.е. присваивает им метки -1 (в таблице они представлены звездочками). Затем она вызывает функцию search для фиктивного ребра 0-0, которая помечает все вершины, содержащиеся в том же компоненте, что и 0 (вторая строка таблицы) — для этого она назначает им неотрицательные значения (в таблице проставлены 0). В данном примере вершины 0, 1, 4 и 9 помечаются значениями от 0 до 3 в этом же порядке. Далее просмотр слева направо обнаруживает не помеченную вершину 2 и вызывает функцию search для фиктивного ребра 2-2 (третья строка таблицы). Функция search помечает семь вершин, содержащихся в том же компоненте, что и 2. При продолжении просмотра слева направо вызывается search для ребра 8-8, и в результате помечаются вершины 8 и 11 (нижняя строка таблицы). После этого функция GRAPHsearch проверяет, что все вершины от 9 до 12 помечены, и завершает поиск.

Программа 18.3 — пример, который показывает, как можно получить класс DFS для определения остовного леса, производный от базового класса SEARCH из программы 18.2. В производный класс добавлен приватный вектор st для хранения представления дерева родительскими ссылками, которое инициализируется в конструкторе. Кроме того, в этом классе определена функция searchC, которая совпадает с функцией searchC из программы 18.1, за исключением того, что она принимает в качестве аргумента ребро v-w и заносит в st[w] значение v. И, наконец, добавлена общедоступная функция-член, которая позволяет клиентам определять родителя любой вершины. Остовные леса применяются во многих приложениях, но в этой главе они нужны нам в основном для понимания динамического поведения DFS, о чем пойдет речь в разделе 18.4.

В связном графе конструктор из программы 18.2 вызывает функцию searchC всего один раз (для ребра 0-0) , после чего обнаруживает, что все остальные вершины помечены. В графе, состоящем из более чем одного связного компонента, конструктор последовательно просматривает все связные компоненты. Поиск в глубину является первым из нескольких методов, который будет применяться для поиска связных компонентов графа. Но независимо от метода (и представления графа), программа 18.2 представляет собой эффективный метод просмотра всех вершин графа.

Программа 18.3. Производный класс для поиска в глубину

Данный код демонстрирует порождение производного от DFS класса для построения остовного дерева на основе базового класса, определенного в разделе 18.2. Конструктор строит представление леса в векторе st (родительские ссылки) и в векторе ord (из базового класса). Клиенты могут использовать объект DFS для определения родителя любой заданной вершины леса (ST) или позиции любой заданной вершины при прямом обходе леса (перегруженный оператор []). Свойства таких лесов и их представлений будут рассмотрены в разделе 18.4.

  template <class Graph>
  class DFS : public SEARCH<Graph>
    { vector<int> st;
      void searchC(Edge e)
        { int w = e.w;
          ord[w] = cnt++; st[e.w] = e.v;
          typename Graph::adjIterator A(G, w);
          for (int t = A.beg(); !A.end(); t = A.nxt())
            if (ord[t] == -1) searchC(Edge(w, t));
        }
    public:
      DFS(const Graph &G) : SEARCH<Graph>(G),
        st(G.V(), -1) { search(); }
      int ST(int v) const { return st[v]; }
    };
      

Функции поиска на графах предоставляют систематический способ обработки каждой вершины и каждого ребра графа. Обычно наши программные реализации построены так, чтобы они отрабатывали за линейное или за примерно линейное время, выполняя фиксированный объем обработки для каждого ребра. Мы докажем этот факт для поиска в глубину, хотя этот же метод доказательства работает и для нескольких других стратегий поиска.

Основной вывод из лемм 18.3 и 18.4 заключается в том, что время выполнения поиска в глубину линейно зависит от размера структуры данных, используемой для представления графа. В большинстве ситуаций можно считать, что время выполнения DFS линейно зависит от размеров самого графа: в случае насыщенного графа (число ребер которого пропорционально V² ) этот результат справедлив для любого представления, а в случае разреженного графа предполагается представление списками смежности. Вообще-то обычно считается, что время выполнения DFS линейно зависит от E. Формально это утверждение неверно — для разреженных графов, представленных матрицей смежности, или для крайне разреженных графов, для которых E << Vи большая часть вершин изолирована; однако обычно нетрудно избежать первой ситуации и удалить изолированные вершины во второй ситуации (см. упражнение 17.34).

Как будет показано ниже, эти рассуждения применимы к любому алгоритму, для которого выполняются некоторые основные свойства DFS. Если алгоритм помечает каждую вершину и проверяет все инцидентные ей вершины (и выполняет другую работу, на выполнение которой для одной вершины требуется время, ограниченное некоторой константой), то для него эти свойства выполняются. В более общей формулировке это звучит так: если время, затрачиваемое на обработку каждой вершины ограничено некоторой функцией f (V, E), то время поиска гарантированно пропорционально E + f (V, E). В разделе 18.8 мы увидим, что поиск в глубину является одним из алгоритмов семейства, которому присущи как раз такие свойства; в лекциях 19—22 мы увидим, что алгоритмы этого семейства лежат в основе значительной части программ, которые рассматриваются в данной книге.

Многие изучаемые нами программы обработки графов представляют собой реализации АТД для каких-то конкретных задач; в них мы разрабатываем класс, выполняющий базовый поиск для вычисления структурной информации в других векторах, индексированных именами вершин. Такой класс можно породить от класса из программы 18.2 или, в более простых случаях, просто заново реализовать поиск. Многие из наших классов обработки графов имеют такой характер, поскольку, при выполнении поиска на графе мы, как привило, получаем представление и о его структуре. Обычно мы добавляем код в функцию поиска, которая выполняется после пометки всех вершин, вместо того чтобы работать с более общим алгоритмом поиска (например, который вызывает указанную функцию при каждом посещении вершины) — просто чтобы сделать код компактным и замкнутым. Построение более общего механизма АТД, который позволяет клиентам обрабатывать все вершины с помощью клиентских функций, является очень полезной практикой (см. упражнения 18.13 и 18.14).

В разделах 18.5 и 18.6 мы познакомимся с многочисленными функциями обработки графов, основанными на DFS. В разделах 18.7 и 18.8 мы рассмотрим другие реализации функции search и ряд других функций обработки графов, основанных на этих реализациях. Мы не встраиваем такой уровень абстракции в наш код, но мы стараемся четко показать базовую стратегию поиска на графе, которая лежит в основе разрабатываемого алгоритма. Например, мы применяем термин класс DFS для любой реализации, основанной на рекурсивной схеме DFS. Примерами классов DFS могут служить класс программ для поиска простого пути (программа 17.16) и класс остовного леса (программа 18.3).

Многие функции обработки графов основаны на использовании векторов, индексируемых именами вершин. Обычно такие векторы включаются в реализации классов как приватные члены данных и содержат информацию о структуре графов (определяемую во время поиска), которая и позволяет решить текущую задачу. Примерами таких векторов могут служить вектор deg в программе 17.11 и вектор ord в программе 18.1. Некоторые из реализаций, которые мы рассмотрим, используют сразу несколько векторов для изучения сложных структурных свойств.

При написании функций поиска на графах мы будем придерживаться следующего соглашения: вначале все векторы, индексируемые именами вершин, очищаются значением — 1, а функции поиска будут заносить во все элементы, соответствующие посещенным вершинам, неотрицательные значения. Любой такой вектор может играть роль вектора ord (пометка вершин как посещенных) в программах 18.2 и 18.3. Если функция поиска на графе основана на использовании или вычислении вектора, индексируемого именами вершин, то зачастую мы просто реализуем поиск и используем этот вектор для пометки вершин, а не порождаем класс от базового класса SEARCH и не задействуем вектор ord.

Конкретные результаты поиска на графе зависят не только от природы функции поиска, но и от представления графа и даже от порядка просмотра вершин функцией search. Для определенности в примерах и упражнениях в данной книге мы будем употреблять термин стандартный DFS по спискам смежности (standard adjacency-lists DFS) для обозначения процесса вставки последовательности ребер в АТД графа, реализованный на основе представления списками смежности (программа 17.9) с последующим выполнением DFS — например, с помощью программы 18.3. В случае представления матрицей смежности порядок вставки ребер не влияет на динамику поиска, но мы будем использовать параллельный термин стандартный DFS по матрице смежности (standard adjacency-matrix DFS) для обозначения процесса вставки последовательности ребер в АТД графа, реализованный на основе представления графа матрицей смежности (программа 17.7) с последующим выполнением DFS — например, с помощью программы 18.3.

Упражнения

18.8. В стиле рис. 18.5 рис. 18.5 приведите трассу вызовов рекурсивной функции, выполняемых при стандартном DFS по матрице смежности для графа

3-71-47-80-55-23-82-90-64-92-66-4.

18.9. В стиле рис. 18.7 рис. 18.7 приведите трассу вызовов рекурсивной функции, выполняемых при стандартном DFS по матрице смежности для графа

3-71-47-80-55-23-82-90-64-92-66-4.

18.10. Измените реализацию АТД графа в виде матрицы смежности (программе 17.7), чтобы в ней использовалась фиктивная вершина, связанная со всеми другими вершинами. Напишите реализацию упрощенного DFS, используя это изменение.

18.11. Выполните упражнение 18.10 для реализации АТД списками смежности (программа 17.9).

18.12. Существует 13! различных перестановок вершин в графе, показанном на рис. 18.8. Какая часть этих перестановок может описывать порядок посещения вершин графа программой 18.2?

18.13. Напишите реализацию клиентской функции АТД графа, которая вызывает указанную клиентом функцию для каждой вершины графа.

18.14. Напишите реализацию клиентской функции АТД графа, которая вызывает указанную клиентом функцию для каждого ребра графа. Такая функция может оказаться приемлемой альтернативой функции GRAPHedges (см. программу 17.2).