|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Виды графов и их свойства
Глоссарий
С графами связана обширная терминология. Большинство употребляемых терминов имеют простые определения, и для удобства ссылок лучше рассмотреть их в каком-то одном месте -а именно, здесь. Некоторые из этих понятий мы уже употребляли при изучении базовых алгоритмов в "Введение" , а другие понадобятся лишь при изучении сложных алгоритмов в лекциях 18—22.
Определение 17.1. Граф (graph) -это некоторое множество вершин (vertex) и некоторое множество ребер (edge), соединяющих пары различных вершин (одну пару вершин может соединять максимум одно ребро).
Если граф состоит из V вершин, то мы будем помечать их числами от 0 до V-1. Основная причина выбора этой системы обозначений заключается в том, что она обеспечивает быстрый доступ к информации, соответствующей каждой вершине, путем индексирования векторов. В разделе 17.6 будет рассмотрена программа, которая использует таблицу символов для установления взаимно-однозначного соответствия V произвольных имен вершин с V целыми числами от 0 до V-1. Пользуясь этой программой, мы можем (для удобства обозначений) употреблять без потери общности индексы как имена вершин. Иногда мы будем предполагать, что множество вершин определено неявно, с помощью множества ребер, учитывая только те вершины, которые упомянуты хотя бы в одном ребре. Во избежание громоздких выражений наподобие " граф из 10 вершин со следующим набором ребер " , мы часто не будем указывать явно количество вершин, если оно понятно из контекста. Далее будем придерживаться соглашения: количество вершин в заданном графе всегда обозначается буквой V, а количество ребер -буквой E.
Мы примем определение 17.1 в качестве стандартного определения графа (мы уже сталкивались с ним в "Рекурсия и деревья" ), но учтите, что в нем использованы два технических упрощения. Во-первых, в нем запрещены одинаковые ребра (математики иногда называют такие ребра параллельными, а граф, который может содержать такие ребра -мультиграфом (multigraph)). Во-вторых, в нем запрещены ребра, соединяющие вершины с собой; такие ребра называются петлями (self-loop). Графы, в которых нет параллельных ребер или петель, иногда называют простыми графами (simple graph).
В наших формальных определениях используются простые графы, поскольку так легче выразить их основные свойства, а, кроме того, параллельные ребра и петли во многих приложениях и не нужны. Например, нетрудно вычислить верхнюю границу количества ребер простого графа с заданным количеством вершин.
Лемма 17.1. Граф, состоящий из Vвершин, содержит не более V(V- 1)/2 ребер.
Доказательство. Общее количество возможных пар вершин равно V2, из них V петель, а ребра между различными вершинами учитываются дважды, следовательно, максимальное количество ребер не превосходит значения
(V2 -V)/2 = V(V-1)/2
. 
Эта верхняя граница недействительна, если допустимы параллельные ребра: не простой граф может содержать лишь две вершины и миллиарды ребер, соединяющие их (или даже одну вершину и миллиарды петель).
В некоторых приложениях удаление параллельных ребер и петель можно рассматривать как задачу обработки данных, которую должны выполнять сами приложения.
В других приложениях проверка, представляет ли заданный набор ребер простой граф, может вообще не иметь смысла. В данной книге там, где удобно рассматривать приложение или разрабатывать алгоритм на основе расширенного определения графа, включающего параллельные ребра или петли, мы будем это делать. Например, петли играют важную роль в классическом алгоритме, описанный в разделе 17.4, а параллельные ребра широко используются в приложениях, которые будут рассмотрены в "Потоки в сетях" . В общем случае из контекста будет ясно, в каком смысле используется термин " граф " - " простой граф " , " мультиграф " или " мультиграф с петлями " .
Математики употребляют термины вершина (vertex) и узел (node) как эквивалентные, но мы будем обычно использовать термин вершина при изучении графов и термин узел при обсуждении представлений графов -например, структур данных в C++. Как правило, мы полагаем, что вершина может иметь имя и другую связанную с ней информацию. Аналогично, для соединений двух вершин математиками широко используются слова дуга (arc), ребро (edge) и связь (link), однако мы всегда будем употреблять термин ребро при изучении графов и термин ссылка при обсуждении структур данных в C++.
Если имеется ребро, соединяющее две вершины, будем говорить, что обе эти вершины смежны (adjacent) друг с другом, а ребро инцидентно (incident) этим вершинам. Степень (degree) вершины -это количество ребер, инцидентных этой вершине. Ребро, соединяющее вершины v и w, мы будем обозначать v-w, либо эквивалентной записью w-v.
Подграф (subgraph) -это подмножество ребер некоторого графа (и связанных с ними вершин), которые сами образуют граф. При решении многих вычислительных задач требуется выделение различных подграфов. Если выделить некоторое подмножество вершин графа и все ребра графа, соединяющие пары вершин этого подмножества, то полученный подграф называется индуцированным (этими вершинами) подграфом (induced subgraph).
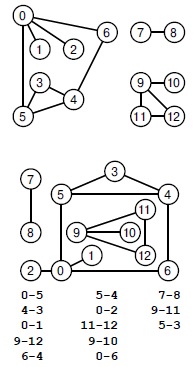
Граф можно начертить, обозначая точками его вершины и соединяя эти точки линиями, которые означают ребра. Такой чертеж может помочь получить представление о структуре графа, но следует помнить, что определение графа дается вне зависимости от его представления. Например, два чертежа и список ребер на рис. 17.1 представляют один и тот же граф, поскольку этот граф -всего лишь (неупорядоченное) множество его вершин и (неупорядоченное) множество его ребер (пар вершин), и ничего более. В принципе достаточно рассматривать граф просто как множество ребер, однако мы рассмотрим и другие представления, которые более удобны в качестве основы для структур данных графов, рассматриваемых в разделе 17.4.
Граф определяется его вершинами и ребрами, но не способом его графического изображения. Оба приведенных чертежа, а также список ребер (внизу) изображают один и тот же граф -при наличии информации, что рассматриваемый граф содержит 13 вершин, помеченных номерами от 0 до 12.
Размещение вершин графа на плоскости и вычерчивание этих вершин и соединяющих их ребер позволяет получить чертеж графа. Возможно множество различных вариантов размещения вершин, стилей изображения ребер и визуального оформления. Алгоритмы построения чертежей, учитывающие различные естественные ограничения, тщательно изучены, и некоторые из них успешно и широко применяются (см. раздел ссылок). Например, одно из простейших ограничений -требование, чтобы ребра не пересекались. Планарный (плоский) граф (planar graph) -это граф, который можно начертить на плоскости без пересечения ребер. Определение, является ли граф планарным, представляет собой увлекательную задачу, которая будет кратко рассмотрена в разделе 17.8. Возможность построения удобного визуального представления графа часто бывает полезна на практике, и поэтому вычерчивание графов -благодатное поле для исследований, хотя построить хороший чертеж графа не всегда просто. Многие графы с очень большим количеством вершин и ребер являются абстрактными объектами, визуально представить которые невозможно.
В некоторых приложениях -например, представляющих в виде графа географические карты или электрические схемы -чертеж графа может содержать существенную информацию, поскольку вершины соответствуют точкам на плоскости, а расстояния между ними должны быть выдержаны в определенном масштабе. Такие графы называются евклидовыми (Euclidean graph). Во множестве других приложений графы могут представлять зависимости или расписания событий, и тогда они просто содержат информацию о связности, не предъявляя никаких требований к геометрическому расположению вершин. Мы рассмотрим примеры алгоритмов, которые используют геометрическую информацию евклидовых графов, в "Минимальные остовные деревья" и 21, но в основном мы будем работать с алгоритмами, которые вообще не используют геометрическую информацию. Еще раз подчеркиваем: обычно графы не зависят от конкретного представления в виде чертежа или данных в компьютере.
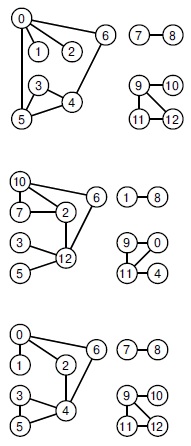
Если сосредоточиться только на связях, то метки вершин можно считать просто удобными обозначениями, а два графа считать одинаковыми, если они отличаются друг от друга только метками вершин. Два графа называются изоморфными (isomorphic), если можно поменять метки вершин в одном из них так, чтобы множество ребер этого графа стало эквивалентным множеству ребер другого графа. Определение изоморфизма двух графов представляет собой сложную вычислительную задачу (см. рис. 17.2 и упражнение 17.5). Ее сложность объясняется тем, что существует V! способов обозначения вершин -слишком много, чтобы перепробовать все возможности.
Два верхних графа изоморфны, поскольку можно переобозначить вершины таким образом, что оба множества ребер станут идентичными (чтобы сделать граф в центре таким же, как и верхний граф, нужно поменять 10 на 4, 7 на 3, 2 на 5, 3 на 1, 12 на 0, 5 на 2, 9 на 11, 0 на 12, 11 на 9, 1 на 7 и 4 на 10). Нижний граф не изоморфен двум другим, поскольку не существует такого способа переименования его вершин, чтобы множество его ребер стало идентично множествам ребер двух первых графов.
Поэтому, несмотря на потенциальную привлекательность уменьшения количества различных структур графа, если рассматривать изоморфные графы как идентичные структуры, это делается редко.
Как и в случае деревьев, рассмотренных в "Рекурсия и деревья" , нас очень часто интересуют базовые структурные свойства, которые можно определить из некоторых последовательностей ребер графа.