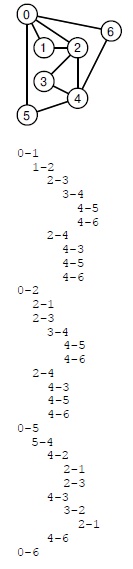|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Виды графов и их свойства
Простые, эйлеровы и гамильтоновы пути
Первые нетривиальные алгоритмы обработки графов, которые мы сейчас рассмотрим, решают фундаментальные задачи, касающиеся поиска путей в графах. В них вводится общий рекурсивный принцип, который будет применяться на протяжении всей книги, и на их примере мы увидим, что с виду очень похожие задачи могут существенно различаться по трудности их решения.
Эти задачи уводят нас от локальных свойств, таких как существование конкретных ребер или определение степеней вершин, к глобальным свойствам, которые могут кое-что сказать о структуре графа. Наиболее фундаментальное свойство графа -связность двух его вершин. Если они связаны, то хотелось бы найти простейший путь, который их связывает.
Простой путь. Если заданы две какие-либо вершины графа, существует ли путь, который их соединяет? В некоторых приложениях достаточно просто знать, существует или нет такой путь, но данном случае наша задача заключается в том, чтобы найти конкретный путь.
Программа 17.16 представляет собой непосредственное решение этой задачи. В ее основу положен поиск в глубину (depth-first search) -фундаментальный принцип обработки графов, на котором мы кратко останавливались в "Элементарные структуры данных" и 5, и который будет подробно рассмотрен в "Поиск на графе" .
Программа 17.16. Поиск простого пути
Этот класс использует рекурсивную функцию поиска в глубину searchR, которая находит простой путь, соединяющий две заданные вершины графа, и предоставляет функцию-член exists, позволяющую клиенту проверить, существует ли путь между вершинами. Для двух заданных вершин v и w функция searchR проверяет каждое ребро v-t, смежное с v, может ли оно быть первым ребром на пути к w. Вектор visited, индексированный именами вершин, предотвращает повторное использование любой вершины, то есть находятся только простые пути.
template <class Graph>
class sPATH
{ const Graph &G;
vector <bool> visited;
bool found;
bool searchR(int v, int w)
{ if ( v == w) return true;
visited[v] = true;
typename Graph::adjIterator A(G, v);
for (int t = A.beg(); !A.end(); t = A.nxt())
if (!visited[t])
if (searchR(t, w)) return true;
return false;
}
public:
sPATH(const Graph &G, int v, int w) :
G(G), visited(G.V(), false)
{ found = searchR(v, w); }
bool exists() const
{ return found; }
};
Этот алгоритм основан на приватной функции-члене, которая определяет, существует ли простой путь из вершины v в вершину w, проверяя для каждого ребра v-t, инцидентного v, существует ли простой путь из t в w, который не проходит через v. В нем используется вектор, индексированный именами вершин, который позволяет отметить v, чтобы ни при каком рекурсивном вызове не проверялся путь, проходящий через v.
Программа 17.16 просто проверяет, существует ли путь. Как можно добавить в нее возможность вывода ребер, составляющих путь? Рекурсивный подход предлагает простое решение:
- Добавить оператор вывода ребра v-t сразу же после того, как рекурсивный вызов в функции searchR находит путь из t в w.
- В вызове функции searchR в конструкторе поменять местами v и w.
Одно лишь первое изменение приводит к тому, что путь из v в w будет выведен в обратном порядке: если вызов searchR(t, w) находит путь из t в w (и выводит составляющие его ребра в обратном порядке), то для вывода пути из v в w остается вывести путь t-v. Второе изменение меняет порядок: чтобы вывести ребра, составляющие путь из v в w, нужно вывести путь из w в v в обратном порядке. (Этот прием годится только для неориентированных графов.) Такую стратегию можно применить и для реализации функции АТД, которая вызывает клиентскую функцию для каждого ребра пути (см. упражнение 17.88).
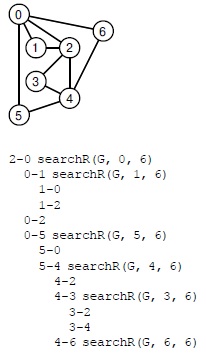
На рис. 17.17 приведен пример динамики рекурсии. Как и в случае любой другой рекурсивной программы (вообще-то любой программы с вызовами функций), получить подобную трассировку нетрудно. Чтобы внести такую возможность в программу 17.16, можно добавить переменную depth для отслеживания глубины рекурсии (ее значение увеличивается на 1 при входе и уменьшается на 1 при выходе), а затем вставить в начало рекурсивной функции код вывода depth пробелов перед нужной информацией (см. упражнения 17.86 и 17.87).
Данная трассировка показывает, как работает рекурсивная функция из программы 17.16при вызове searchR(G, 2.6) для поиска простого пути из вершины 2 в вершину 6 на графе, который показан в верхней части рисунка. Для каждого рассматриваемого ребра выводится отдельная строка с отступом на один уровень больше для каждого рекурсивного вызова. Для проверки ребра 2-0 нужен вызов searchR(G,0,6). Для его завершения необходимо проверить ребра 0-1, 0-2 и 0-5. Для проверки ребра 0-1 нужен вызов searchR(G, 1.6) -для его завершения необходимо проверить ребра 1-0 и 1-2, которые не приводят к рекурсивным вызовам, поскольку вершины 0 и 2 уже помечены. В этом примере функция находит путь 2-0-5-4-6.
Лемма 17.2. Путь, соединяющий две заданных вершины графа, можно найти за линейное время.
Рекурсивная функция поиска в глубину из программы 17.16 представляет собой доказательство по индукции, что функция АТД определяет, существует ли искомый путь. Это доказательство легко расширить, чтобы установить, что в худшем случае программа 17.16 проверяет все элементы матрицы смежности в точности один раз. Аналогично можно показать, что подобная программа для списков смежности проверяет в худшем случае все ребра графа в точности два раза (по разу в каждом направлении). 
Когда в контексте алгоритмов на графах мы используем термин линейное (linear), это означает, что количественное значение не превосходит величины V+E (размер графа), умноженной на некоторый постоянный коэффициент. Как было сказано в конце раздела 17.5, такое значение также обычно не превосходит размера представления графа, умноженного на некоторый постоянный коэффициент. Формулировка свойства 17.2 позволяет, как обычно, использовать представление списками смежности для разреженных графов и представление матрицей смежности для насыщенных графов. Термин " линейный " нельзя применять для описания алгоритма, который использует матрицу смежности и выполняется за время, пропорциональное V2 (даже если он линеен по отношению к размеру представления графа) -кроме случаев, когда граф является насыщенным. Вообще-то при представлении разреженного графа матрицей смежности линейный по времени алгоритм невозможен для любой задачи обработки графов, в которой нужно перебрать все ребра.
Мы детально разберем поведение поиска в глубину в более общей форме в следующем разделе, там же мы рассмотрим несколько других алгоритмов связности. Например, слегка более общая версия программы 17.16 дает способ перебора всех ребер графа и построения вектора, индексированного именами вершин, который позволяет клиенту проверить за постоянное время, существует ли путь, соединяющий какие-либо две вершины.
Лемма 17.2 дает существенно завышенную оценку реального времени работы программы 17.16 -ведь она может найти путь, просмотрев лишь нескольких ребер. Но пока нам достаточно знать лишь то, что существует метод, который гарантированно находит путь, соединяющий любую пару вершин любого графа за линейное время. Однако другие, с виду похожие, задачи решить намного труднее. Например, рассмотрим следующую задачу, когда нужно найти путь, соединяющий пару вершин, но при условии, что этот путь проходит через все остальные вершины графа.
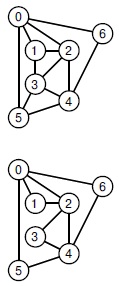
В графе, приведенном вверху, имеется гамильтонов цикл 0-6-4-2-1-3-5-0, который проходит через каждую вершину точно один раз и возвращается в первоначальную вершину. В нижнем графе такого цикла нет.
Гамильтонов путь. Существует ли простой путь, соединяющий две заданные вершины, который проходит через каждую вершину графа в точности один раз? Если этот путь должен возвратиться в исходную вершину, то эта задача называется задачей поиска гамильтонова цикла ( рис. 17.18). Существует ли цикл, который проходит через каждую вершину в точности один раз?
На первый взгляд кажется, что эта задача решается просто, достаточно внести некоторые простые изменения в рекурсивную часть класса поиска пути в программе 17.16. Однако такая программа непригодна для многих графов, поскольку время ее выполнения в худшем случае экспоненциально зависит от количества вершин в графе.
Лемма 17.3. Рекурсивный поиск гамильтонова цикла может потребовать экспоненциального времени.
Доказательство. Рассмотрим граф, у которого (V-1)-я вершина изолирована, а ребра, связывающие остальные V—1 вершин, образуют полный граф. Программа 17.17 не найдет гамильтонов путь, но по индукции легко видеть, что она перебирает все (V-1)! путей в полном графе, каждый из которых требует V—1 рекурсивных вызовов (
рис.
17.19). Следовательно, общее количество рекурсивных вызовов равно V! или примерно
(V/e)V
, что больше любой константы в степени V. 
Эта трассировка показывает ребра, просмотренные программой 17.17 для определения, что граф, приведенный вверху, не имеет гамильтонова цикла. Для краткости ребра, входящие в помеченные вершины, опущены.
Полученные нами реализации -программа 17.16 для поиска простых путей, и программа 17.17 для поиска гамильтоновых путей -очень похожи друг на друга. При отсутствии путей выполнение обеих программ прекращается, когда все элементы вектора visited становятся равными true. Но почему времена выполнения этих программ так разительно отличаются? Программа 17.16 гарантированно выполняется за короткое время, поскольку она заносит true по крайней мере в один элемент вектора visited при каждом вызове searchR. А программа 17.17 может снова сбрасывать элементы вектора visited, поэтому гарантировать ее быстрое выполнение невозможно.
При поиске простых путей программой 17.16 мы знаем, что если существует путь из v в w, то его можно найти, выбрав одно из ребер v-t, исходящих из v; то же самое верно и в отношении гамильтоновых путей. Но на этом сходство заканчивается.