Поразрядный поиск

Программа 15.7. Поиск и вставка в R-путевом trie-дереве существования

В данной реализации операций найти и вставить АТД таблицы существования для многопутевых trie-деревьев ключи хранятся неявно внутри структуры trie-дерева. Каждый узел содержит R указателей на следующий, более низкий уровень trie-дерева. Если t-я цифра ключа равна i, происходит переход на уровне t по i-ой ссылке. Функция поиска возвращает фиктивный элемент, содержащий переданный в аргументе ключ, если он присутствует в таблице, или nullItem в противном случае. В качестве альтернативы можно было бы изменить интерфейс, чтобы в нем использовался только тип Key, или в созданном классе элементов реализовать преобразование типа из Item в Key.

  private:
    struct node
    { node **next;
      node()
        { next = new node*[R];
          for (int i = 0; i < R; i++) next[i] = 0;
        }
    };
  typedef node *link;
  link head;
  Item searchR(link h, Key v, int d)
    { int i = digit(v, d);
      if (h == 0) return nullItem;
      if (i == NULLdigit)
        { Item dummy(v); return dummy; }
      return searchR(h->next[i], v, d+1);
    }
    void insertR(link& h, Item x, int d)
      { int i = digit(x.key(), d);
        if (h == 0) h = new node;
        if (i == NULLdigit) return;
        insertR(h->next[i], x, d+1);
      }
    public:
      ST(int maxN)
      { head = 0; }
    Item search(Key v)
      { return searchR(head, v, 0); }
    void insert(Item x)
      { insertR(head, x, 0); }
      

Предположим, например, что используется типичное значение R = 256 и имеется N случайных 64-разрядных ключей. В соответствии с леммой 15.6 для выполнения поиска потребуется lgN / 8 сравнений символов (максимум 8), и при этом будет задействовано менее 47 N ссылок. Если объем доступной памяти не ограничен, этот метод является весьма эффективной альтернативой. А взяв в этом примере R = 65536, можно сократить затраты на выполнение поиска до 4 сравнений символов, однако при этом потребуется более 5900 N ссылок.

Мы вернемся к стандартным многопутевым деревьям в разделе 15.5. Далее до конца этого раздела рассматривается альтернативное представление trie-деревьев, построенных программой 15.7: trie-дерево тернарного поиска (ternary search trie — TST), или просто TST-дерево, полная форма которого показана на рис. 15.16.

Рис. 15.16. Структуры trie-деревьев существования

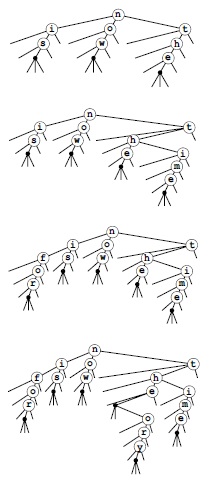
На этих рисунках показаны три различных реализации trie-дерева существования для 16 слов call me ishmael some years ago never mind how long precisely having little or no money: 26-путевое trie-дерево существования (вверху), абстрактное trie-дерево с удаленными пустыми ссылками (в центре) и представление TST-деревом (внизу). 26-путевое trie-дерево содержит слишком много ссылок, но TST-дерево служит эффективным представлением абстрактного trie-дерева.

В двух верхних trie-деревьях предполагается, что ни один ключ не является префиксом другого. Например, добавление ключа not привело бы к потере ключа no. Для решения этой проблемы в конец каждого ключа можно добавить нулевой символ, как показано в TST-дереве на нижнем рисунке.

В TST-дереве каждый узел содержит символ и три ссылки, соответствующие ключам, текущие цифры которых меньше, равны или больше символа этого узла.

Этот подход эквивалентен реализации узлов trie-дерева в виде BST-деревьев, в которых в качестве ключей используются символы, соответствующие непустым ссылкам. В стандартных trie-деревьях существования из программы 15.7 узлы trie-дерева представляются R + 1 ссылками, и символы, представленные каждой непустой ссылкой, определяются их индексами. В соответствующем TST-дереве существования все символы, соответствующие непустым ссылкам, явно присутствуют в узлах: мы находим символы, соответствующие ключам, только проходя по средним ссылкам.

Алгоритм поиска для реализации АТД таблицы существования на основе TST-деревьев настолько прост, что его нетрудно написать самостоятельно. Алгоритм вставки несколько сложнее, но в точности соответствует вставке в trie-деревьях существования. В начале поиска первый символ ключа сравнивается с символом в корне. Если он меньше, поиск продолжается по левой ссылке, если больше — по правой, а если равен, поиск проходит по средней ссылке, и выполняется переход к следующему символу ключа. В любом случае алгоритм продолжается рекурсивно. Поиск завершается неудачно, если встретилась пустая ссылка или ключ поиска закончился раньше, чем в дереве встретился символ NULLdigit. Поиск завершается успешно, если происходит переход по средней ссылке с символом NULLdigit. Для вставки нового ключа выполняется поиск, а затем добавляются новые узлы для символов в заключительной части ключа — точно так же, как и в trie-деревьях. Подробности реализации этих алгоритмов приведены в программе 15.8, а на рис. 15.17 показаны TST-деревья, соответствующие trie-деревьям на рис. 15.15.

Рис. 15.17. TST-деревья существования

TST-дерево существования содержит по одному узлу для каждой буквы, но каждый узел имеет только 3 дочерних узла, а не 26. Деревья на трех верхних рисунках — это TST-деревья, соответствующие примеру вставки на рис. 15.15 рис. 15.15, за исключением того, что к каждому ключу дописан завершающий символ. Это позволяет снять ограничение, что ни один ключ не может быть префиксом другого. Теперь можно, например, вставить ключ theory (рисунок внизу).

Продолжая использовать соответствие между деревьями поиска и алгоритмами сортировки, мы видим, что TST-деревья соответствуют трехпутевой поразрядной сортировке, так же, как BST-деревья соответствуют быстрой сортировке, trie-деревья — бинарной быстрой сортировке, а М-путевые trie-деревья — М-путевой поразрядной сортировке. Структура рекурсивных вызовов для трехпутевой поразрядной сортировки, показанная на рис. 10.12, представляет собой TST-дерево для этого набора ключей. Проблема пустых ссылок, присущая trie-деревьям, соответствует проблеме пустых контейнеров поразрядной сортировки; трехпутевое ветвление обеспечивает эффективное решение обеих этих проблем.

Программа 15.8. Поиск и вставка в TST-дереве существования

Это код реализует те же алгоритмы абстрактного trie-дерева, что и в программе 15.7, но каждый узел содержит лишь одну цифру и три ссылки: по одной для ключей, следующая цифра которых меньше, равна и больше соответствующей цифры в искомом ключе.

  private:
    struct node
    { Item item; int d; node *l, *m, *r;
      node(int k)
        { d = k; l = 0; m = 0; r = 0; }
    };
  typedef node *link;
  link head;
  Item nullItem;
  Item searchR(link h, Key v, int d)
    { int i = digit(v, d);
      if (h == 0) return nullItem;
      if (i == NULLdigit)
        { Item dummy(v); return dummy; }
      if (i < h->d) return searchR(h->l, v, d);
      if (i == h->d) return searchR(h->m, v, d+1);
      if (i > h->d) return searchR(h->r, v, d);
    }
    void insertR(link& h, Item x, int d)
      { int i = digit(x.key(), d);
        if (h == 0) h = new node(i);
        if (i == NULLdigit) return;
        if (i < h->d) insertR(h->l, x, d);
        if (i == h->d) insertR(h->m, x, d+1);
        if (i > h->d) insertR(h->r, x, d);
      }
    public:
      ST(int maxN)
      { head = 0; }
    Item search(Key v)
      { return searchR(head, v, 0); }
    void insert(Item x)
      { insertR(head, x, 0); }
      

Эффективность использования памяти TST-деревьями можно повысить, помещая ключи в листья в тех точках, где они различны, и сворачивая однонаправленные пути между внутренними узлами, как в patricia-деревьях. В конце этого раздела мы рассмотрим реализацию, основанную на первом из этих изменений.

Рис. 15.18. Пример строковых ключей (номеров вызовов библиотечных функций)

Эти ключи из онлайновой библиотечной базы данных иллюстрируют гибкость структуры, обеспечиваемую в приложениях обработки строковых ключей. Некоторые символы могут быть смоделированы случайными буквами, другие — случайными цифрами, а третьи имеют фиксированное значение или структуру.

Главное достоинство TST-деревьев заключается в том, что они аккуратно приспосабливаются к неоднородностям в ключах, которые весьма вероятны в реальных приложениях. Это проявляется в виде двух основных эффектов. Во-первых, ключи в реальных приложениях берутся из больших символьных наборов, а использование конкретных символов из набора далеко от однородного — например, в конкретном наборе строк, скорее всего, будет использоваться лишь небольшая часть возможных символов. Используя TST-деревья, можно применять 256-символьную ASCII-кодировку или даже 65536-символьный Unicode, не беспокоясь о лишних затратах в узлах с 256- или 65536-путевым ветвлением и не задумываясь, какие наборы символов действительно применяются. Unicode-строки символов алфавитов, отличных от латинского, могут содержать тысячи символов — TST-деревья особенно подходят для строковых ключей, состоящих из таких символов. Во-вторых, в реальных приложениях ключи часто имеют структурированный формат, различный в разных приложениях, когда в одной части ключа используются только буквы, в другой — только цифры, а в качестве разделителей используются специальные символы (см. упражнение 15.72). Например, на рис. 15.18 приведен список номеров вызовов онлайновой библиотечной базы данных. В случае таких ключей некоторые из узлов trie-дерева могут быть представлены унарными узлами в TST-дереве (там, где все ключи содержат разделители), другие могут быть представлены BST-деревьями, состоящими из 10 узлов (там, где все ключи содержат цифры), а третьи — BST-деревьями из 26 узлов (там, где все ключи содержат буквы). Эта структура создается автоматически, без какого-либо специального анализа ключей.

Второе практическое достоинство поиска, основанного на TST-деревьях, по сравнению с множеством других алгоритмов заключается в том, что неудачные поиски обычно исключительно эффективны даже при длинных ключах. Часто для завершения неудачного поиска алгоритм использует лишь несколько сравнений байтов (и проходит по нескольким ссылкам). Как было показано в разделе 15.3, для неудачного поиска в хеш-таблице, содержащей N ключей, требуется время, пропорциональное длине ключа (для вычисления хеш-функции), а в дереве поиска требуется не менее lgN сравнений ключей. Даже в patricia-дереве для неудачного поиска случайного ключа требуетсяlgN сравнений разрядов.