Поразрядный поиск

Многопутевые trie-деревья и TST-деревья

Мы уже видели, что производительность поразрядной сортировки можно существенно увеличить, рассматривая одновременно более чем один разряд. То же самое справедливо и в отношении поразрядного поиска: сравнивая одновременно по r разрядов, скорость поиска можно увеличить в r раз. Однако здесь есть скрытая опасность, из-за которой эту идею следует применять более осторожно, чем в случае поразрядной сортировки. Проблема заключается в том, что одновременное сравнение r разрядов соответствует использованию узлов дерева с R = 2^r ссылками, а это может привести к значительным излишним затратам памяти на неиспользуемые ссылки.

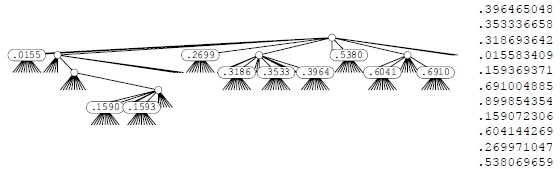
В (бинарных) trie-деревьях, описанных в разделе 15.2, узлы, соответствующие разрядам ключей, имеют две ссылки: одну для нулевого разряда ключа, и вторую — для единичного. Естественно обобщить их до R-путевых trie-деревьев, в которых цифрам ключа соответствуют узлы с R ссылками, по одной для каждого возможного значения цифры. Ключи хранятся в листьях (узлах со всеми пустыми ссылками). Поиск в R-путевом trie-дереве начинается с корня и с самой левой цифры ключа, и цифры ключа используются для управления спуском по дереву. Если значение цифры равно i, выполняется переход по i-ой ссылке (и на следующую цифру). Если обнаружен лист, он содержит единственный ключ в trie-дереве, ведущие цифры которого соответствуют пройденному пути, поэтому для определения того, успешно или неудачно завершился поиск, остается сравнить этот ключ с искомым. При достижении пустой ссылки понятно, что поиск неудачен, поскольку эта ссылка соответствует последовательности ведущих цифр, не найденной ни в одном ключе trie-дерева. На рис. 15.14 показано 10-путевое trie-дерево, представляющее некоторое множество десятичных чисел.

Рис. 15.14. R-путевое trie-дерево для десятичных чисел

На этом рисунке показано trie-дерево, которое позволяет различать набор чисел (см. рис. 12.1). Каждый узел имеет 10 ссылок (по одной для каждой возможной цифры). Ссылка 0 в корне указывает на trie-дерево для ключей, первая цифра которых равна 0 (есть только одно такое число); ссылка 1 указывает на trie-дерево для ключей с первой цифрой 1 (таких деревьев два) и т.д. Ни одно из этих чисел не начинается с цифр 4, 7, 8 или 9, поэтому соответствующие ссылки остаются пустыми. В дереве присутствует только по одному числу, первая цифра которого равна 0, 2 и 5, поэтому для каждой из этих цифр имеется лист, содержащий соответствующее число. Остальная часть структуры построена рекурсивно, переходя каждый раз на одну цифру вправо.

Как отмечалось в главе 10 "Поразрядная сортировка" , встречающиеся на практике числа обычно различаются сравнительно небольшим количеством узлов trie-дерева. Эта же особенность для более общих типов ключей служит основой для ряда эффективных алгоритмов поиска.

Прежде чем создавать полную реализацию таблицы символов с несколькими типами узлов, мы начнем изучение многопутевых деревьев с задачи таблицы существования, в которой хранятся только ключи (без записей или связанной с ними информации). Требуется разработать алгоритмы операций вставки ключа в структуру данных и поиска в структуре данных, чтобы определить, был ли уже вставлен заданный ключ. Чтобы использовать тот же интерфейс, что и для более общих реализаций таблиц символов, мы будем придерживаться соглашения, что функция поиска возвращает nullItem в случае неудачи и фиктивный элемент, содержащий искомый ключ, в случае успеха. Это соглашение упрощает код и способствует наглядному представлению структуры многопутевых trie-деревьев. В разделе 15.5 будут рассмотрены более общие реализации таблиц символов, в том числе индексы строк.

Для простоты в этом определении предполагается, что ни один ключ не является префиксом другого. Обычно это ограничение достигается при условии, что все ключи различны и либо имеют фиксированную длину, либо содержат завершающий символ со значением NULLdigit — сигнальный символ, который не используется ни для каких других целей. Суть данного определения в том, что таблицы существования можно реализовать с помощью trie-деревьев существования, не храня внутри trie-дерева никакой информации. Вся информация неявно определяется структурой trie-дерева. Каждый узел содержит R + 1 ссылку (по одной для каждой возможной цифры плюс одна ссылка для NULLdigit) и не содержит никакой другой информации. Для управления спуском по trie-дереву во время поиска используются цифры ключа. Если ссылка на NULLdigit встретилась одновременно с завершением цифр ключа, то поиск успешен, иначе — неудачен. Для вставки нового ключа поиск выполняется до тех пор, пока не встретится пустая ссылка, а затем добавляются узлы для каждого из оставшихся символов ключа. На рис. 15.15 показан пример 27-путевого trie-дерева; программа 15.7 содержит реализацию базовых процедур поиска и вставки в (многопутевом) trie-дереве существования.

Если ключи имеют фиксированную длину и различны, можно обойтись без конечного символа и прекращать поиск при достижении конца ключа (см. упражнение 15.55). Мы уже встречались с примером подобного trie-дерева, когда использовали trie-деревья для описания MSD-сортировки ключей фиксированной длины (см. рис. 10.10).

В некотором смысле это чисто абстрактное представление структуры trie-дерева является оптимальным, т.к. оно может поддерживать выполнение операции найти за время, пропорциональное длине ключа, при затратах памяти, в худшем случае пропорциональных количеству всех символов в ключе. Однако общий объем используемой памяти может оказаться весьма большим, поскольку для каждого символа нужно около R ссылок, поэтому необходимы более эффективные реализации. Как было показано для случая бинарных trie-деревьев, чистую структуру trie-дерева удобно рассматривать как конкретное представление базовой абстрактной структуры, являющейся хорошо определенным представлением используемого набора ключей, а затем рассмотреть и другие представления той же абстрактной структуры, которые могут обеспечить лучшую производительность.

Предполагается, что ключи в структуре данных различны, и ни один ключ не является префиксом другого. При выполнении поиска в стандартном многопутевом trie-дереве цифры ключа используются для управления поиском при спуске по дереву, при этом возможны три варианта. Если достигнута пустая ссылка, значит, поиск неудачен; если достигнут лист, содержащий ключ поиска, то поиск успешен; и если достигнут лист, содержащий другой ключ — поиск неудачен. Все листья имеют R пустых ссылок, поэтому, как было сказано в разделе 15.2, узлы-листья и не листовые узлы удобно представить по-разному. Такая реализация будет рассмотрена в "Внешний поиск" , а в этой главе предлагается другой подход. В любом случае можно обобщить аналитические результаты из раздела 15.3 и получить представление о характеристиках производительности стандартных многопутевых деревьев.

Рис. 15.15. Поиск и вставка в R-путевом trie-дереве существования

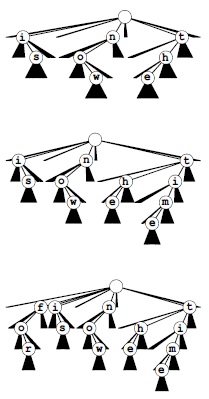
26-путевое trie-дерево для слов now, is и the (вверху) имеет девять узлов: корень плюс по одному узлу для каждой буквы. Здесь узлы помечены буквами, но в этой структуре данных не нужны явные метки узлов, поскольку метка каждого узла может быть получена, исходя из позиции его ссылки в массиве ссылок родительского узла. При вставке ключа time в существующем узле для буквы t создается новая ветка, и добавляются новые узлы для букв i, m и e (в центре); для вставки ключа for создается новая ветка от корня, и добавляются новые узлы для букв f, o и r.

Характеристики производительности, указанные в лемме 15.6, представляют собой крайний случай компромисса между временем и памятью. С одной стороны, имеется большое количество неиспользуемых пустых ссылок — лишь несколько узлов вблизи вершины дерева используют более одной-двух из своих ссылок. Зато, с другой стороны, высота дерева получается небольшой.