|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Таблицы символов и деревья бинарного поиска
Характеристики производительности деревьев бинарного поиска
Время выполнения алгоритмов, работающих с BST-деревьями, зависит от формы деревьев. В лучшем случае дерево может быть идеально сбалансированным и содержать приблизительно lgN узлов между корнем и каждым из внешних узлов, но в худшем случае путь поиска может содержать N узлов.
Можно также надеяться, что время поиска в среднем также будет логарифмическим, поскольку первый вставляемый элемент становится корнем дерева: если N ключей должны быть вставлены в произвольном порядке, то этот элемент должен поделить ключи пополам (в среднем), что дает логарифмическое время поиска (рассуждая аналогично по всем поддеревьям). Действительно, возможен случай, когда BST-дерево приводит в точности к тем же сравнениям, что и бинарный поиск (см. упражнение 12.58). Этот случай был бы наилучшим для данного алгоритма, гарантируя логарифмическое время выполнения для любого поиска. В действительно произвольной ситуации корнем может быть любой ключ, поэтому идеально сбалансированные деревья встречаются исключительно редко, и сохранять дерево полностью сбалансированным после каждой вставки нелегко. Однако полностью несбалансированные деревья для случайных ключей также встречаются редко, поэтому в среднем деревья достаточно хорошо сбалансированы. В этом разделе мы детализируем это наблюдение.
Оказывается, длина пути и высота бинарных деревьев, рассмотренные в "Рекурсия и деревья" , непосредственно связаны с затратами на поиск в BST-деревьях. Высота определяет затраты на поиск в худшем случае, длина внутреннего пути непосредственно связана с затратами при успешном поиске, а длина внешнего пути непосредственно связана с затратами при неудачном поиске.
Лемма 12.6. В дереве бинарного поиска, образованном N случайными ключами, для успешного поиска в среднем требуется около 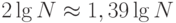 сравнений.
сравнений.
Как было сказано в разделе 12.3, мы считаем последовательные операции ==и < одной операцией сравнения. Количество сравнений, нужных для успешного поиска, завершающегося в данном узле, равно 1 плюс расстояние от этого узла до корня. Просуммировав эти расстояния по всем узлам дерева, мы получим его внутреннюю длину пути. Таким образом, интересующая нас величина равна 1 плюс средняя длина внутреннего пути BST-дерева, которую можно проанализировать с помощью уже знакомых рассуждений: если CN - средняя длина внутреннего пути BST-дерева, состоящего из N узлов, то верно следующее рекуррентное соотношение:
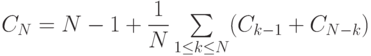 ,
,
при C1 = 1. Член N - 1 учитывает, что корень увеличивает длину пути для каждого из остальных N - 1 узлов на 1; остальная часть выражения следует из того, что ключ в корне (вставленный первым) с равной вероятностью может быть k-ым по величине ключом, разбивая дерево на случайные поддеревья размерами k - 1 и N-k. Это рекуррентное соотношение почти идентично тому, которое было решено в
"Быстрая сортировка"
для быстрой сортировки, и его можно решить тем же способом, получив искомый результат. 
Лемма 12.7. В дереве бинарного поиска, образованном N случайными ключами, для вставок и неудачного поиска в среднем требуется около 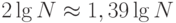 сравнений.
сравнений.
Поиск произвольного ключа в дереве, содержащем N узлов, с равной вероятностью может завершиться неудачей в любом из N + 1 внешних узлов. Это свойство в сочетании с тем фактом, что разница длин внешнего и внутреннего пути в любом дереве равна просто 2N (см. лемму 5.7), и дает искомый результат. В любом BST-дереве среднее количество сравнений, необходимых для выполнения вставки или неудачного поиска, приблизительно на 1 больше среднего количества сравнений, необходимых для успешного поиска. 
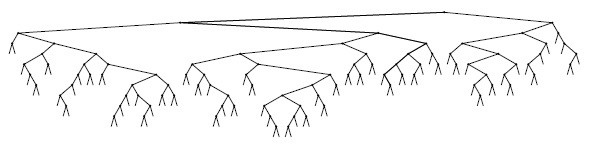
В соответствии с леммой 12.6 следует ожидать, что затраты на поиск для BST-деревьев должны быть приблизительно на 39% выше затрат для бинарного поиска для случайных ключей. Но в соответствии с леммой 12.7 эти дополнительные затраты вполне окупаются, поскольку новый ключ может быть вставлен почти при тех же затратах - бинарному поиску подобная гибкость недоступна. На рис. 12.8 показано BST-дерево, полученное из длинной последовательности случайных перестановок. Оно содержит несколько длинных и несколько коротких путей, но все-таки его можно считать хорошо сбалансированным: для выполнения любого поиска требуется менее 12 сравнений, а среднее количество сравнений, необходимых для успешного поиска произвольного элемента, равно 7,00, при 5,74 для бинарного поиска.
Леммы 12.6 и 12.7 определяют производительность в среднем при условии, что ключи расположены в произвольном порядке. Если это не так, производительность алгоритма может ухудшиться.
Лемма 12.8. Для поиска в дереве бинарного поиска с N ключами в худшем случае может потребоваться N сравнений.
На
рис.
12.9 и 12.10 показаны два примера худших случаев BST-деревьев. Для этих деревьев поиск с использованием бинарного дерева ничем не лучше последовательного поиска в односвязных списках. 
Таким образом, высокая производительность базовой реализации таблиц символов на основе BST-дерева достигается тогда, когда ключи достаточно случайны, и, значит, дерево не содержит длинных путей. К сожалению, на практике худший случай встречается не столь уж редко - он возникает при вставке прямо или обратно упорядоченных ключей в первоначально пустое дерево с применением стандартного алгоритма - т.е. при последовательности операций, которую мы вполне можем предпринять, не получив никакого явного предупреждения по этому поводу.
В этом BST-дереве, которое было построено вставками около 200 произвольных ключей в первоначально пустое дерево, ни один поиск не использует более 12 сравнений. Средняя стоимость успешного поиска приблизительно равна 10.
Если ключи вставляются в BST-дерево в порядке возрастания, дерево вырождается в форму, эквивалентную односвязному списку, что приводит к квадратичному времени создания дерева и к линейному времени поиска.
Множество других вариантов вставки ключей также приводят к вырождению BST-дерева. Однако дерево бинарного поиска, образованное произвольно упорядоченными ключами, скорее всего, окажется хорошо сбалансированным.
В главе 13 "Сбалансированные деревья" будут рассмотрены способы превращения этого худшего случая в крайне маловероятный, полного исключения худшего случая и превращения всех деревьев в деревья как для лучшего случая, где длины всех путей гарантированно логарифмические.
Ни одна из других рассмотренных реализаций таблиц символов не может использоваться для выполнения задачи вставки в таблицу очень большого количества произвольных ключей, а затем поиска каждого из них - время выполнения каждого из методов, описанных в разделах 12.2-12.4, для этой задачи квадратично. Более того, анализ показывает, что среднее расстояние до узла в бинарном дереве пропорционально логарифму количества узлов в дереве - как мы вскоре увидим, это позволяет эффективно выполнять вперемешку операции поиска, вставки и другие операции АТД таблицы символов.
Упражнения
12.56. Напишите рекурсивную программу, которая вычисляет максимальное количество сравнений, требуемых для любого поиска в данном BST-дереве (высоту дерева).
12.57. Напишите рекурсивную программу, которая вычисляет среднее количество сравнений, требуемых для успешного поиска в данном BST-дереве (длину внутреннего пути дерева, деленную на N).
12.58. Приведите такую последовательность вставок ключей E A S Y Q U E S T I O N в первоначально пустое BST-дерево, чтобы созданное при этом дерево было эквивалентно бинарному поиску - в том смысле, что последовательность сравнений, выполняемых при поиске любого ключа в BST-дереве, совпадали бы с последовательностью сравнений, выполняемых при бинарном поиске на том же множестве ключей.
12.59. Напишите программу, которая вставляет набор ключей в первоначально пустое BST-дерево так, чтобы созданное дерево было эквивалентно бинарному поиску, в смысле, описанном в упражнении 12.58.
12.60. Нарисуйте все различные по структуре BST-деревья, которые могут образоваться после вставки N ключей в первоначально пустое дерево, для 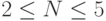 .
.
12.61. Для каждого из деревьев из упражнения 12.60 определите вероятность того, что оно получится в результате вставки N произвольных различных элементов в первоначально пустое дерево.
12.62. Сколько бинарных деревьев, состоящих из N узлов, имеют высоту N? Сколько существует различных способов вставки N различных ключей в первоначально пустое дерево, приводящих к образованию BST-дерева с высотой N ?
12.63. Докажите методом индукции, что разница между длинами внешнего и внутреннего путей в любом бинарном дереве составляет 2N (см. лемму 5.7).
12.64. Определите эмпирически среднее значение и среднеквадратичное отклонение количества сравнений при успешных и неудачных поисках в BST-дереве, созданном вставкой N случайных ключей в первоначально пустое дерево, для N = 103, 104, 105 и 106 .
12.65. Напишите программу, которая строит t BST-деревьев вставкой N случайных ключей в первоначально пустое дерево и вычисляет максимальную высоту дерева (максимальное количество сравнений, необходимых для неудачного поиска при вставке в любом из этих t деревьев), для N = 103, 104, 105 и 106 при t = 10, 100 и 1000.