Схемы из функциональных элементов
Теорема 10. Существует схема размера  , осуществляющая сложение
двух
, осуществляющая сложение
двух  -битовых чисел.
-битовых чисел.
Напомним смысл обозначения  : нам надо построить
схему сложения
: нам надо построить
схему сложения  -битовых чисел, имеющую размер не
более
-битовых чисел, имеющую размер не
более 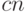 для некоторого
для некоторого  и для
всех
и для
всех  .
.
Вспомним, как складывают числа в столбик:

 ,
а бит переноса равен
,
а бит переноса равен  , если хотя
бы два из этих трех битов равны
, если хотя
бы два из этих трех битов равны  ). Поэтому можно составить
схему, которая вычисляет эти биты справа налево и имеет размер
). Поэтому можно составить
схему, которая вычисляет эти биты справа налево и имеет размер  .
.Заметим, что теорему 9 легко вывести из
теоремы 10: чтобы сравнить числа  и
и  , сложим число
, сложим число 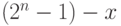 (то есть число
(то есть число  , в котором все
единицы заменены нулями и наоборот) и число
, в котором все
единицы заменены нулями и наоборот) и число  . Если в старшем
разряде появится единица, то
. Если в старшем
разряде появится единица, то  , а если нет, то
, а если нет, то  .
Остается заметить, что и сложение, и обращение битов в числе
.
Остается заметить, что и сложение, и обращение битов в числе  требуют схем линейного размера. Таким образом, сравнение чисел
сводится к вычислению бита переноса. Верно и обратное:
вычисление бита переноса сводится к сравнению двух чисел
(обратим в одном из слагаемых все биты).
требуют схем линейного размера. Таким образом, сравнение чисел
сводится к вычислению бита переноса. Верно и обратное:
вычисление бита переноса сводится к сравнению двух чисел
(обратим в одном из слагаемых все биты).
Тем не менее конструкция, использованная при доказательстве
теоремы 9, имеет некоторые преимущества. Назовем глубиной схемы максимальное число
элементов на пути от входа к выходу. Если представить себе, что
сигнал на выходе элемента появляется не сразу после подачи
сигналов на входы, а с некоторой задержкой, то глубина схемы
определяет суммарную задержку. Легко понять, что рекурсивная
схема сравнения имела глубину  (число уровней
пропорционально логарифму размера входа), в то время как
построенная только что схема сложения имеет глубину,
пропорциональную
(число уровней
пропорционально логарифму размера входа), в то время как
построенная только что схема сложения имеет глубину,
пропорциональную  (биты переноса вычисляются последовательно,
справа налево). Но можно соединить эти два результата:
(биты переноса вычисляются последовательно,
справа налево). Но можно соединить эти два результата:
Теорема 11. Существует схема сложения двух  -битовых чисел размера
-битовых чисел размера  и глубины
и глубины  .
.
Как мы видели, проблема в том, что биты переноса вычисляются
последовательно, а не параллельно. Если удастся их все
вычислить схемой размера  и глубины
и глубины  ,
то дальнейшее очевидно.
,
то дальнейшее очевидно.
Как мы упоминали, вычисление битов переноса равносильно
сравнению, так что для доказательства теоремы достаточно
научиться сравнивать параллельно все "суффиксы"двух  -битовых
чисел
-битовых
чисел 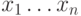 и
и 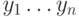 , т. е. для
каждого
, т. е. для
каждого  сравнить числа
сравнить числа 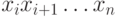 и
и 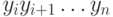 .
.
Вспомним, что мы делали при сравнении чисел (скажем, длины  ).
На нижнем уровне мы сравнивали биты:
).
На нижнем уровне мы сравнивали биты:
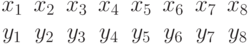
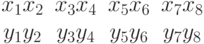
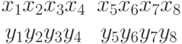
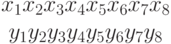
 ,
, 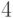 ,
,  и
и  результаты сравнения уже есть. Для суффикса длины
результаты сравнения уже есть. Для суффикса длины  результат
можно получить, комбинируя результат сравнения
результат
можно получить, комбинируя результат сравнения 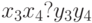 и
и 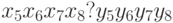 . После этого у нас есть
информация о суффиксах всех четных длин, и соединяя ее с
информацией с первого этапа, получаем сведения про все суффиксы.
Например, для сравнения суффиксов длины
. После этого у нас есть
информация о суффиксах всех четных длин, и соединяя ее с
информацией с первого этапа, получаем сведения про все суффиксы.
Например, для сравнения суффиксов длины  , то есть
, то есть 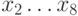 и
и 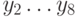 , мы соединяем
результаты сравнения
, мы соединяем
результаты сравнения  и
и 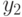 с результатами
сравнения суффиксов длины
с результатами
сравнения суффиксов длины  , то есть
, то есть 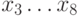 и
и 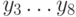 .
.В общем случае картина такая: после "сужающегося дерева"
мы строим "расширяющееся"; за  шагов до конца мы знаем
результаты сравнения всех суффиксов, длины которых кратны
шагов до конца мы знаем
результаты сравнения всех суффиксов, длины которых кратны 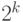 .
Это дерево имеет размер
.
Это дерево имеет размер  и глубину
и глубину  ,
что завершает доказательство.
,
что завершает доказательство.
14. Покажите, что вычитание двух  -битовых чисел по модулю
-битовых чисел по модулю 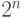 выполняется схемой размера
выполняется схемой размера  и глубины
и глубины  .
(Указание: вычитание легко сводится к сложению, если заменить нули на единицы и наоборот.)
.
(Указание: вычитание легко сводится к сложению, если заменить нули на единицы и наоборот.)
Теперь займемся умножением. Схема умножения двух  -разрядных
чисел имеет
-разрядных
чисел имеет  входов (по
входов (по  для каждого множителя) и
для каждого множителя) и  выходов для произведения.
выходов для произведения.
Посмотрим, какие оценки дает обычный способ умножения чисел
столбиком. В нем умножение двух  -разрядных чисел сводится к
сложению
-разрядных чисел сводится к
сложению  копий первого числа (частично замененных на нули в
зависимости от цифр второго числа) со сдвигами.
копий первого числа (частично замененных на нули в
зависимости от цифр второго числа) со сдвигами.
Получение этих копий требует схемы размера 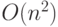 (общее число
цифр в копиях) и глубины
(общее число
цифр в копиях) и глубины 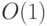 . Сложение двух
. Сложение двух  -разрядных
чисел мы можем выполнить с помощью схемы размера
-разрядных
чисел мы можем выполнить с помощью схемы размера  и
глубины
и
глубины  , так что необходимые
, так что необходимые 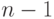 сложений
можно выполнить схемой размера
сложений
можно выполнить схемой размера 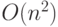 и глубины
и глубины 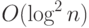 (если
складывать сначала попарно, потом результаты снова попарно и т. д.).
Оказывается, этот результат можно улучшить. Наиболее
экономные способы основаны на преобразовании Фурье (о них можно
прочесть в книге [1]). С их
помощью, например, можно построить схему умножения
(если
складывать сначала попарно, потом результаты снова попарно и т. д.).
Оказывается, этот результат можно улучшить. Наиболее
экономные способы основаны на преобразовании Фурье (о них можно
прочесть в книге [1]). С их
помощью, например, можно построить схему умножения  -битовых
чисел, имеющую размер
-битовых
чисел, имеющую размер  .
.
Эти методы далеко выходят за рамки нашего обсуждения, но два улучшения мы приведем.
Теорема 12. Существует схема умножения двух  -разрядных
чисел размера
-разрядных
чисел размера 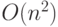 и глубины
и глубины  .
.
Как мы уже говорили, умножение двух  -разрядных чисел
сводится к сложению
-разрядных чисел
сводится к сложению  таких чисел, и остается выполнить такое
сложение схемой размера
таких чисел, и остается выполнить такое
сложение схемой размера 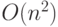 и глубины
и глубины  .
Ключевым моментом здесь является сведение сложения трех чисел к сложению
двух с помощью простой схемы размера
.
Ключевым моментом здесь является сведение сложения трех чисел к сложению
двух с помощью простой схемы размера  и
глубины
и
глубины 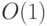 . В самом деле, пусть есть три числа
. В самом деле, пусть есть три числа  ,
,  и
и  . Если мы будем складывать отдельно в каждом разряде, то в разряде может
накопиться любая сумма от
. Если мы будем складывать отдельно в каждом разряде, то в разряде может
накопиться любая сумма от  до
до  , то есть в двоичной
записи от
, то есть в двоичной
записи от  до
до  . Сформируем из младших битов этих
двухбитовых сумм число
. Сформируем из младших битов этих
двухбитовых сумм число  , а из старших (сдвинутых влево) — число
, а из старших (сдвинутых влево) — число  . Тогда, очевидно,
. Тогда, очевидно, 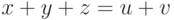 . Получение цифр числа
. Получение цифр числа  и
и  происходит параллельно во всех разрядах и требует размера
происходит параллельно во всех разрядах и требует размера  и глубины
и глубины 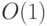 .
.
Теперь, если надо сложить  чисел, можно разбить их на тройки
и из каждых трех чисел получить по два. В следующий круг, таким
образом, выйдут
чисел, можно разбить их на тройки
и из каждых трех чисел получить по два. В следующий круг, таким
образом, выйдут 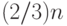 чисел (примерно — граничные эффекты
большой роли не играют). Их снова можно сгруппировать по тройкам и т. д.
С каждым уровнем число слагаемых убывает в полтора раза,
так что глубина схемы будет логарифмической. Каждое
преобразование трех слагаемых в два требует схемы размера
чисел (примерно — граничные эффекты
большой роли не играют). Их снова можно сгруппировать по тройкам и т. д.
С каждым уровнем число слагаемых убывает в полтора раза,
так что глубина схемы будет логарифмической. Каждое
преобразование трех слагаемых в два требует схемы размера  и уменьшает число слагаемых на единицу, так что потребуется
и уменьшает число слагаемых на единицу, так что потребуется  таких преобразований. Итак, эта конструкция имеет общий размер
таких преобразований. Итак, эта конструкция имеет общий размер 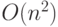 и глубину
и глубину  . Надо только отметить,
что в конце у нас получается не одно число, а два, и их напоследок
надо сложить — что мы умеем делать с глубиной
. Надо только отметить,
что в конце у нас получается не одно число, а два, и их напоследок
надо сложить — что мы умеем делать с глубиной  и
размером
и
размером  .
.
15. Докажите, что схема, вычисляющая булеву функцию  от
от  аргументов, у которой ни один аргумент не является фиктивным,
имеет размер не менее
аргументов, у которой ни один аргумент не является фиктивным,
имеет размер не менее 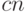 и глубину не менее
и глубину не менее  ,
где
,
где  — некоторая константа, зависящая от выбранного набора
элементов. (Аргумент функции называют фиктивным, если от него значение функции не зависит.)
— некоторая константа, зависящая от выбранного набора
элементов. (Аргумент функции называют фиктивным, если от него значение функции не зависит.)
Эта задача показывает, что если в процессе умножения двух  -разрядных
чисел мы суммируем
-разрядных
чисел мы суммируем  слагаемых размера
слагаемых размера  ,
то оценки
,
то оценки 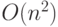 для размера и
для размера и  для глубины,
полученные при доказательстве теоремы 12, существенно улучшить нельзя.
для глубины,
полученные при доказательстве теоремы 12, существенно улучшить нельзя.
Однако никто не обязывает нас следовать традиционному способу умножения столбиком — отказавшись от него, мы можем уменьшить размер схемы.
