Схемы из функциональных элементов
Теорема 7. Пусть 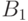 и
и 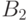 — два полных набора булевых
функций. Тогда соответствующие меры сложности отличаются не более чем на постоянный множитель:
найдется такое число
— два полных набора булевых
функций. Тогда соответствующие меры сложности отличаются не более чем на постоянный множитель:
найдется такое число  , что
, что 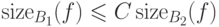 и
и 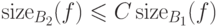 для любой функции
для любой функции  .
.
Утверждение почти очевидно: поскольку наборы 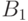 и
и 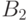 полны, то каждая функция одного из наборов
может быть вычислена какой-то схемой,
составленной из элементов другого набора. Теперь можно
взять в качестве
полны, то каждая функция одного из наборов
может быть вычислена какой-то схемой,
составленной из элементов другого набора. Теперь можно
взять в качестве  наибольший размер таких схем,
и неравенства будут выполняться: каждую строку
программы можно заменить на
наибольший размер таких схем,
и неравенства будут выполняться: каждую строку
программы можно заменить на  (или меньше) строк с
использованием функций другого набора.
(или меньше) строк с
использованием функций другого набора.
Что можно сказать о сложности произвольной булевой функции  аргументов? Следующая теорема показывает, что она
экспоненциально зависит от
аргументов? Следующая теорема показывает, что она
экспоненциально зависит от  (для "наугад взятой"функции).
(для "наугад взятой"функции).
Теорема 8. (а) Пусть  . Тогда сложность любой булевой функции
. Тогда сложность любой булевой функции  аргументов не превосходит
аргументов не превосходит 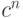 для всех достаточно
больших
для всех достаточно
больших  . (б) Пусть
. (б) Пусть  . Тогда
сложность большинства булевых функций
. Тогда
сложность большинства булевых функций  аргументов
не меньше
аргументов
не меньше 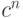 для всех достаточно больших
для всех достаточно больших  .
.
Прежде всего заметим, что по предыдущей теореме не имеет значения,
какой полный базис выбрать (изменение значения  более
существенно, чем умножение сложности на константу).
более
существенно, чем умножение сложности на константу).
Первое утверждение теоремы очевидно: размер схемы, реализующей
дизъюнктивную нормальную форму с  переменными, есть
переменными, есть 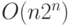 , поскольку имеется не более
, поскольку имеется не более 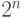 конъюнктов
размера
конъюнктов
размера  . (Напомним смысл
. (Напомним смысл  -обозначений:
-обозначений: 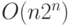 означает, что существует верхняя оценка вида
означает, что существует верхняя оценка вида 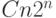 для некоторой
константы
для некоторой
константы  .) Осталось заметить, что
.) Осталось заметить, что 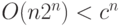 при
достаточно больших
при
достаточно больших  (напомним, что
(напомним, что  ).
).
Чтобы доказать второе утверждение, оценим число различных схем
(скажем, в базисе И, ИЛИ, НЕ) размера  с
с  аргументами. Каждая такая схема может быть
описана последовательностью из
аргументами. Каждая такая схема может быть
описана последовательностью из  присваиваний, выражающих одну из
переменных через предыдущие. Для каждого присваивания есть не более
присваиваний, выражающих одну из
переменных через предыдущие. Для каждого присваивания есть не более 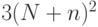 вариантов (три типа операций — конъюнкция,
дизъюнкция, отрицание, и каждый из не более чем двух аргументов
выбирается среди не более чем
вариантов (три типа операций — конъюнкция,
дизъюнкция, отрицание, и каждый из не более чем двух аргументов
выбирается среди не более чем  вариантов). Отсюда легко
получить оценку
вариантов). Отсюда легко
получить оценку  на число всех функций сложности не
более
на число всех функций сложности не
более  (считая
(считая 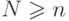 ).
).
Всего булевых функций с  аргументами имеется
аргументами имеется 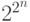 . Из сравнения этих формул видно, что что при
. Из сравнения этих формул видно, что что при  и при достаточно
больших
и при достаточно
больших  булевы функции сложности меньше
булевы функции сложности меньше 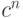 составляют меньшинство, так как
составляют меньшинство, так как 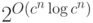 много меньше
много меньше 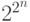 .
.
12. Проведите вторую часть рассуждения более подробно и покажите, что
при некотором 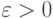 сложность большинства булевых
функций с
сложность большинства булевых
функций с  аргументами не меньше
аргументами не меньше  .
.
Верхнюю оценку в теореме 8 можно усилить и
показать, что сложность любой булевой функции  аргументов не
превосходит
аргументов не
превосходит 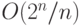 .
.
13. (a) Покажите, что можно построить схему
размера  с
с 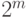 выходами, реализующую
все
выходами, реализующую
все 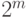 возможных
конъюнктов длины
возможных
конъюнктов длины  (для каждого— свой выход). (Указание:
такую схему можно построить индуктивно.) (б) Покажите, что можно построить схему размера
(для каждого— свой выход). (Указание:
такую схему можно построить индуктивно.) (б) Покажите, что можно построить схему размера  с
с  выходами, реализующую
все
выходами, реализующую
все  булевых функций
булевых функций  аргументов. (Указание: эту схему также
можно построить индуктивно.) (в) Пусть
аргументов. (Указание: эту схему также
можно построить индуктивно.) (в) Пусть 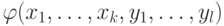 —
булева функция, аргументы которой разбиты на две группы.
Покажите, что ее можно записать в виде дизъюнкции
—
булева функция, аргументы которой разбиты на две группы.
Покажите, что ее можно записать в виде дизъюнкции 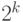 членов,
каждый из которых имеет вид
членов,
каждый из которых имеет вид 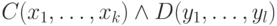 , где
, где  — конъюнкт, а
— конъюнкт, а  —
произвольная булева функция. Вывести отсюда упомянутую выше
оценку
—
произвольная булева функция. Вывести отсюда упомянутую выше
оценку 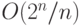 . (Указание: разумно положить
. (Указание: разумно положить 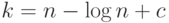 ,
,  . См. также [9] и [33].)
. См. также [9] и [33].)
Теорема 8, однако, ничего не говорит о сложности конкретных булевых функций. Ситуация здесь такова. Есть разнообразные методы и приемы получения верхних оценок. Но про нижние оценки неизвестно практически ничего. Про многие функции мы подозреваем, что их сложность велика (экспоненциально зависит от числа входов), но доказать это пока не удается. Весьма нетривиальные идеи позволяют доказывать экспоненциальные нижние оценки для некоторых специальных классов схем, например, схем из монотонных элементов или схем ограниченной глубины (использующих элементы И и ИЛИ с произвольным числом входов). Получение экспоненциальных оценок для более общих схем — один из возможных подходов к знаменитой проблеме перебора, центральной проблеме теории сложности вычислений.
Мы не будем углубляться в эту теорию, а приведем лишь несколько верхних оценок для конкретных задач. При этом мы не претендуем на полноту, а хотим лишь показать несколько интересных идей и приемов.
Рассмотрим функцию сравнения двух  -битовых чисел.
Она имеет
-битовых чисел.
Она имеет  аргументов (
аргументов (  для
одного числа и
для
одного числа и  для другого); ее значение равно
для другого); ее значение равно  ,
если первое число больше второго, и
,
если первое число больше второго, и  в противном случае.
в противном случае.
Обозначим эту функцию 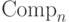 .
.
Теорема 9. Пусть  — полный набор функций. Существует такая
константа
— полный набор функций. Существует такая
константа  , что
, что 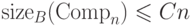 .
.
Заметим, что поскольку в формулировке теоремы оценка размера проводится с точностью до константы, то выбор конкретного базиса не имеет значения. Другими словами, мы можем предполагать, что любое конечное число необходимых нам функций в этом базисе есть.
Схема сравнения чисел будет рекурсивной (чтобы
сравнить два числа, мы отдельно сравниваем их левые и
правые половины, а затем объединяем результаты). При
этом, как часто бывает, надо усилить утверждение,
чтобы индукция прошла. А именно, мы будем строить
схему с  входами
входами 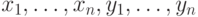 и
двумя выходами, которая указывает, какой из трех
случаев
и
двумя выходами, которая указывает, какой из трех
случаев 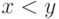 ,
, 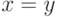 или
или  имеет место.
(Здесь
имеет место.
(Здесь 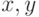 — числа, записываемое в двоичной системе как
— числа, записываемое в двоичной системе как 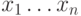 и
и 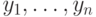 .) Два выходных бита
кодируют четыре возможности, а нужно только три, так что есть
некоторый запас. Для определенности можно считать,
что первый выходной бит истинен, если числа равны, а
второй — если
.) Два выходных бита
кодируют четыре возможности, а нужно только три, так что есть
некоторый запас. Для определенности можно считать,
что первый выходной бит истинен, если числа равны, а
второй — если 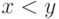 . Тогда возможны три варианта
сигналов на выходе:
. Тогда возможны три варианта
сигналов на выходе:  (равенство),
(равенство), 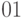 (при
(при 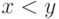 ) и
) и  (при
(при 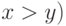 .
.
Объясним теперь, как собрать, скажем, схему сравнения
двух 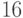 -разрядных чисел. Соберем отдельно
схему сравнения старших
-разрядных чисел. Соберем отдельно
схему сравнения старших  разрядов и младших
разрядов и младших  разрядов. Каждая из них даст ответ в форме
двух битов. Теперь из этих четырех битов надо
собрать два. (Если в старших разрядах неравенство,
то оно определяет результат сравнения; если старшие
разряды равны, то результат сравнения определяется
младшими разрядами.) Написанная в скобках фраза
определяет булеву функцию с четырьмя битами на входе и
двумя битами на выходе, и может быть реализована
некоторой схемой фиксированного размера. Таким образом,
если через
разрядов. Каждая из них даст ответ в форме
двух битов. Теперь из этих четырех битов надо
собрать два. (Если в старших разрядах неравенство,
то оно определяет результат сравнения; если старшие
разряды равны, то результат сравнения определяется
младшими разрядами.) Написанная в скобках фраза
определяет булеву функцию с четырьмя битами на входе и
двумя битами на выходе, и может быть реализована
некоторой схемой фиксированного размера. Таким образом,
если через 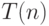 обозначить размер схемы, сравнивающей
обозначить размер схемы, сравнивающей  -битовые числа, то получаем оценку
-битовые числа, то получаем оценку 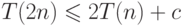 ,
где
,
где  — некоторая константа, зависящая от выбора
базиса. Отсюда следует, что
— некоторая константа, зависящая от выбора
базиса. Отсюда следует, что 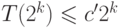 при некотором
при некотором 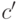 . Всамом деле, для достаточно
большого
. Всамом деле, для достаточно
большого 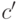 можно доказать по индукции, что
можно доказать по индукции, что  (мы должны усилить неравенство, вычтя из правой части
(мы должны усилить неравенство, вычтя из правой части  , чтобы индуктивный шаг прошел; база индукции
остается верной, если
, чтобы индуктивный шаг прошел; база индукции
остается верной, если 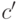 достаточно велико).
достаточно велико).
Ту же самую оценку можно объяснить и наглядно. Наша схема имеет вид иерархического дерева. На каждом уровне из двух двухбитовых сигналов получается один. Остается вспомнить, что в полном двоичном дереве число внутренних вершин (которое определяет размер схемы) на единицу меньше числа листьев. (В турнире по олимпийской системе число игр на единицу меньше числа команд, так как после каждой игры одна команда выбывает.)
Все внутренние вершины и все листья (где
сравниваются два бита) представляют собой схемы
ограниченного размера, откуда и вытекает оценка 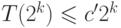 .
.
Осталось лишь сказать, что делать, если размер чисел (который мы
обозначали через  ) не есть точная степень двойки. В этом
случае можно увеличить размер до ближайшей сверху степени двойки
(не более чем в два раза) и подать на старшие разряды входов
нули. Оба действия приводят к увеличению размера схемы не более
чем в константу раз.
) не есть точная степень двойки. В этом
случае можно увеличить размер до ближайшей сверху степени двойки
(не более чем в два раза) и подать на старшие разряды входов
нули. Оба действия приводят к увеличению размера схемы не более
чем в константу раз.
Перейдем к сложению двух  -разрядных чисел.
(Строго говоря, тут возникает не булева функция, а функция
-разрядных чисел.
(Строго говоря, тут возникает не булева функция, а функция 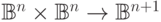 , но все наши определения
очевидно переносятся на этот случай.)
, но все наши определения
очевидно переносятся на этот случай.)
