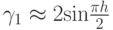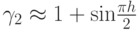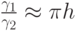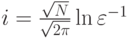Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
6.3. Попеременно - треугольный итерационный метод
При аппроксимации уравнений Пуассона или Лапласа получается система сеточных уравнений

без ограничения общности считаем оператор (матрицу системы) самосопряженным и
положительно определенным. Сеточный оператор Лапласа самосопряжен — это легко доказать, но отрицателен. Для того чтобы получить систему уравнений с положительным оператором, достаточно правую и левую части системы умножить на - 1. Здесь  — квадратная матрица размером N x N.
— квадратная матрица размером N x N.
Зададим матрицу 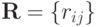 :
:
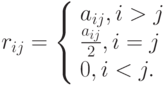
В таком случае  можно представить в виде суммы двух треугольных матриц
можно представить в виде суммы двух треугольных матриц 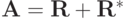 .
.
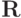 и
и 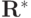 — нижняя и верхняя треугольные матрицы, а их диагональные элементы совпадают. Далее будем рассматривать систему сеточных уравнений как операторное уравнение в конечномерном
евклидовом пространстве (унитарном в комплексном случае).
— нижняя и верхняя треугольные матрицы, а их диагональные элементы совпадают. Далее будем рассматривать систему сеточных уравнений как операторное уравнение в конечномерном
евклидовом пространстве (унитарном в комплексном случае).
Попеременно - треугольный итерационный метод (ПТИМ) может быть представлен в каноническом виде
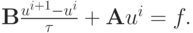
Здесь 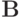 — самосопряженный положительный оператор. Его часто называют оператором предобуславливания. Для рассматриваемого метода оператор предобуславливания представляется в виде произведения
— самосопряженный положительный оператор. Его часто называют оператором предобуславливания. Для рассматриваемого метода оператор предобуславливания представляется в виде произведения

где 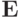 — единичный оператор,
— единичный оператор,  — параметр (действительное число).
— параметр (действительное число).
При известных  и
и  значение uk + 1 находится в два этапа. Сначала вычисляется невязка на итерации
значение uk + 1 находится в два этапа. Сначала вычисляется невязка на итерации 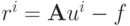 , а затем решается система матричных уравнений
, а затем решается система матричных уравнений
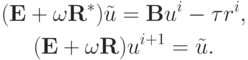
Поскольку матрицы  и
и 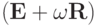 являются треугольными, то эти уравнения решаются значительно проще, чем исходное.
являются треугольными, то эти уравнения решаются значительно проще, чем исходное.
Для формулирования теоремы о ПТИМ введем понятие операторного неравенства:
будем полагать, что  , если для любой сеточной функции, не равной нулю тождественно, выполнено неравенство
, если для любой сеточной функции, не равной нулю тождественно, выполнено неравенство

Теорема (без доказательства). Пусть 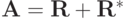 и существуют положительные постоянные
и существуют положительные постоянные  и
и  при которых выполнены неравенства
при которых выполнены неравенства

Пусть также

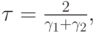
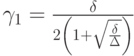
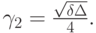
Тогда двухэтапный итерационный метод

сходится, причем для его погрешности справедлива оценка
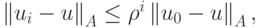
где
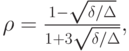
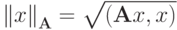 .
.В качестве  можно взять минимальное собственное значение
можно взять минимальное собственное значение  оператора
оператора  , либо любую положительную постоянную
, либо любую положительную постоянную  . Можно показать, что
. Можно показать, что 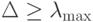 ,
,  , где
, где  — максимальное собственное значение оператора
— максимальное собственное значение оператора  .
.
Рассмотрим применение ПТИМ к численному решению уравнения Пуассона (знак минус ставим для удобства записи):
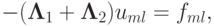
с нулевыми граничными условиями
um0 = umN = u0l = uNl = 0.
Эта задача может быть представлена как операторное уравнение, где  . Оператор будет самосопряженным и положительным.
. Оператор будет самосопряженным и положительным.
Далее необходимо представить матрицу  в виде
в виде 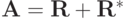 и определить константы
и определить константы  и
и 
Рассмотрим разностную аппроксимацию уравнения Пуассона по схеме "крест", переписав схему в эквивалентном виде:
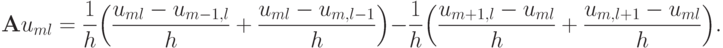
Тем самым представили оператор  как сумму двух операторов
как сумму двух операторов 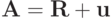 , где
, где
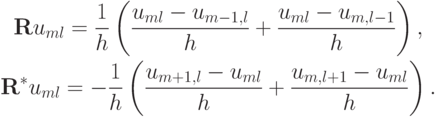
При этом матрица оператора 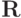 является нижней треугольной, а матрица
является нижней треугольной, а матрица 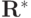 — верхней треугольной (в этом легко убедиться, записав рассматриваемую систему в виде СЛАУ). Можно также показать, что
оператор
— верхней треугольной (в этом легко убедиться, записав рассматриваемую систему в виде СЛАУ). Можно также показать, что
оператор  является сопряженным оператором к
является сопряженным оператором к 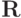 , т.е.
, т.е.  .
.
Также показывается, что

Воспользовавшись формулами для  и
и 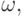 получим
получим
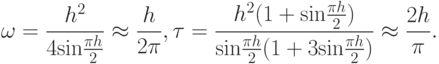
Оценка количества итераций для этого метода дает
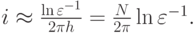
Напомним, что границы спектра для рассматриваемого оператора 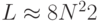 ,
,
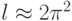
 .
.Алгоритм вычисления 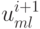 , в соответствии с ранее приведенными формулами двух этапов ПТИМ будет таков.
, в соответствии с ранее приведенными формулами двух этапов ПТИМ будет таков.
Первый этап:
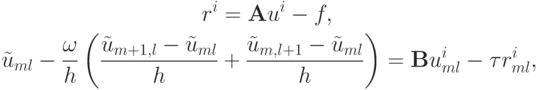
второй этап:
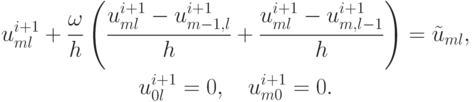
Уравнение для  нужно начинать решать от точки m = N - 1, l = N - 1, учитывая, что на границе сеточной области сеточная функция равна нулю. Таким образом, вычисления ведутся рекуррентно.
Система решается, начиная с правого верхнего угла области до левого нижнего угла. Система линейных уравнений, соответствующая второму этапу, решается аналогично, но вычисления здесь начинаются в точке m = 1, l = 1 и заканчивается в точке m = N - 1, l = N - 1.
нужно начинать решать от точки m = N - 1, l = N - 1, учитывая, что на границе сеточной области сеточная функция равна нулю. Таким образом, вычисления ведутся рекуррентно.
Система решается, начиная с правого верхнего угла области до левого нижнего угла. Система линейных уравнений, соответствующая второму этапу, решается аналогично, но вычисления здесь начинаются в точке m = 1, l = 1 и заканчивается в точке m = N - 1, l = N - 1.
Метод по своим идеям напоминает схему Саульева, рассмотренную ранее в одномерном варианте при решении уравнений параболического типа.
Использование в ПТИМ набора чебышевских итерационных параметров приводит к следующему результату. Расчетные формулы для метода таковы:
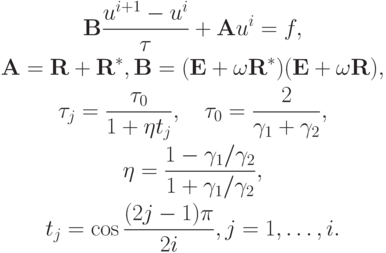
Для проведенного примера