Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1282 / 292 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Специальности: Математик
Лекция 6:
Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
6.7 Задачи
- В современных формулировках метод релаксации рассматривается с черно - белым (шахматным, красно - черным) упорядочением узлов. Назовем все внутренние узлы сетки черными, если для них сумма значений индексов четная, все прочие внутренние узлы назовем белыми. Получить расчетные формулы метода верхней релаксации для сетки с черно - белым (шахматным, красно - черным) упорядочением узлов.
Решение. Заметим, что при расчетах белые узлы соседствуют только с черными, и наоборот. Тогда с учетом этого расчетные формулы будут для всех белых узлов
![\frac{u_{m - 1, l}^{i} + u_{m, l - 1}^{i}}{h^2} + \frac{u_{m, l + 1}^{i} + u_{m + 1, l}^{i}}{h^2} - \frac{4}{h^2} \left[\frac{u_{ml}^{i + 1}}{\tau} +
(1 - \frac{1}{\tau})u_{ml}^{i}\right] = f_{ml},](/sites/default/files/tex_cache/1e7df0897bb835aa490a2ef839ab125f.png)
а для всех черных
![\frac{u_{m - 1, l}^{i + 1} + u_{m, l - 1}^{i + 1}}{h^2} +
\frac{u_{m, l + 1}^{i + 1} + u_{m + 1, l}^{i + 1}}{h^2} - \frac{4}{h^2} \left[\frac{u_{ml}^{i + 1}}{\tau} + (1 - \frac{1}{\tau})u_{ml}^{i}\right] = f_{ml},](/sites/default/files/tex_cache/73c8c8cb8838159b62e8a26ae363af2a.png)
Последовательность вычислений для такого варианта будет несколько отличаться от первоначальной формулировки метода релаксаций. Сначала ищется значение на следующей итерации для всех белых узлов, затем — для черных. Такой итерационный метод очевидным образом связан со схемой "классики" для решения параболических уравнений.
- Пусть число внутренних узлов равно 9. Выписать в матричном виде сеточные уравнения при классической формулировке схемы "крест" и для случая черно - белого упорядочения узлов. Для простоты рассмотреть вариант, когда значения функции на границе области равны нулю.
Решение.
В "классическом" варианте сеточная система есть
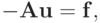
где
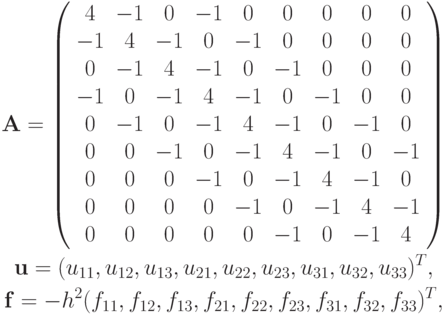
а в случае черно - белого упорядочения узлов сетки
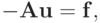
где