Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
6.8. Задачи для самостоятельного решения
- Будем рассматривать только частные типы краевых задач для поля
 , зависящего от двух пространственных переменных (x, y), удовлетворяющего уравнению
, зависящего от двух пространственных переменных (x, y), удовлетворяющего уравнению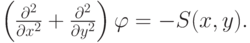
В задачах электростатики
 — это потенциал, а S соответствует плотности заряда; в стационарной тепловой задаче
— это потенциал, а S соответствует плотности заряда; в стационарной тепловой задаче  — температура, S — локальная скорость выделения или поглощения тепла. Будут рассматриваться граничные условия Дирихле, в которых значения
— температура, S — локальная скорость выделения или поглощения тепла. Будут рассматриваться граничные условия Дирихле, в которых значения  задаются на некоторой замкнутой кривой в плоскости (x, y) и, возможно, на некоторых дополнительных кривых внутри области.
задаются на некоторой замкнутой кривой в плоскости (x, y) и, возможно, на некоторых дополнительных кривых внутри области.Реализовать численные алгоритмы, основанные на:
- непосредственной аппроксимации дифференциального оператора и решении системы сеточных уравнений методом Гаусса;
- применении итерационного алгоритма.
- Для уравнения Лапласа,
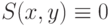 , рассмотреть численное решение для простейших граничных условий (типа констант или линейных функций).
, рассмотреть численное решение для простейших граничных условий (типа констант или линейных функций). - Для уравнения Пуассона вычислить разность потенциалов между двумя зарядами как функцию расстояния между ними и сравнить полученные значения с аналитическими.
- Изменить программу так, чтобы можно было задавать на некоторых внешних и внутренних границах условия Неймана. Изучить решения с такими граничными условиями.
- Вместо граничных условий Дирихле задаются периодические граничные условия. Тогда потенциалы на левой и правой, а также на верхней и нижней границах области
произвольные, но равные по величине друг другу. Т.е. для всех i и j
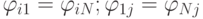 . Уравнения с такими условиями описывают пространственно - периодическое распределение плотности заряда в кристалле. Модифицировать программу и решить уравнение Пуассона с этими граничными условиями.
. Уравнения с такими условиями описывают пространственно - периодическое распределение плотности заряда в кристалле. Модифицировать программу и решить уравнение Пуассона с этими граничными условиями.
- Для уравнения Лапласа,
- Для решения приведенной выше задачи с различными граничными условиями реализовать алгоритм быстрого дискретного преобразования Фурье (алгоритмы такого преобразования описаны, например, в [16.4], [16.8]).
-
Модель малярной кисти Подробнее об этой задаче и других примерах установившихся течений жидкости в [16.13, С. 232 - 240].
При окраске стены кистью, часть краски остается на стенке в виде слоя за кистью. Рассмотрим приближенную модель процесса. Предположим, что кисть состоит из большого числа параллельных и равноотстоящих друг от друга пластин, которые совместно скользят по плоской стенке, в направлении их контакта со стенкой вдоль оси x. Предположим, что пластины имеют бесконечные размеры в направлениях осей x и z, так что результирующее движение представляет собой установившееся течение одного направления. Уравнение движения имеет вид
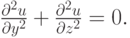
Здесь u — скорость течения жидкости.
Оси координат удобно связать с пластинами, тогда граничные условия для течения в канале между двумя соседними пластинами будут
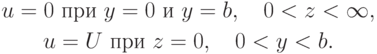
- Получить численное решение поставленной задачи. Сравнить результат с точным
решением

Объяснить, как реализован алгоритм для вычисления значений функции точного решения.
- Получить оценку толщины слоя жидкости, который будет оставаться на стенке позади кисти, при предположении, что все пластины имеют заднюю кромку при одном и том же значении x. Использовать формулу для объемного расхода жидкости, вытекающей из одного канала:Сравнить со значением для точного решения
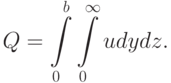
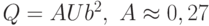 .
. - Указать недостатки рассмотренной модели. Определить характер их влияния на решение.
- Получить численное решение поставленной задачи. Сравнить результат с точным
решением
-
Стационарное движение несжимаемой вязкой жидкости в цилиндрических трубах
Рассмотрим движение несжимаемой вязкой жидкости в цилиндрической трубе произвольного поперечного сечения. Обозначая градиент давления
получим уравнение движения в виде , где
, где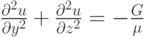
 —
коэффициент вязкости, u — скорость течения жидкости. Требуется решить уравнение, подчиняющееся граничным условиям, с помощью которых задаются градиент давления и значения u при определенных y и z.
—
коэффициент вязкости, u — скорость течения жидкости. Требуется решить уравнение, подчиняющееся граничным условиям, с помощью которых задаются градиент давления и значения u при определенных y и z.
- Решить задачу для трубы круглого поперечного сечения, для которой u = 0 на границе трубы, т.е. при
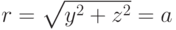 . Сравнить численные результаты с точным решением . Получить численно величину объемного расхода жидкости через произвольное сечение
. Сравнить численные результаты с точным решением . Получить численно величину объемного расхода жидкости через произвольное сечение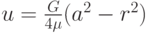 , сравнить ее с точным значением
, сравнить ее с точным значением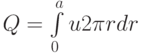 . Предложить, как можно использовать данную величину для контроля точности численного расчета.
. Предложить, как можно использовать данную величину для контроля точности численного расчета.
- Получить решение задачи для трубы эллиптического поперечного сечения с
полуосями B (по оси y ) и C (вдоль оси z ). Сравнить результат численного решения с точным распределением скорости
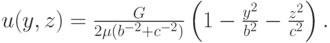
Самостоятельно вывести величину объемного расхода жидкости и сравнить ее точное значение с численными данными.
- Вычислить распределение скорости в трубе прямоугольного поперечного сечения со сторонами y = mb, z = mc (для определенности пусть c > b ). Получить точное решение для скорости и расхода, сравнить его с численным значением.
Указание. Для получения точного решения учесть, что разность
представляет собой четную функцию как от y, так и от z, которая удовлетворяет уравнению Лапласа и равна 0 при y = mb.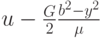
- Решить задачу для трубы круглого поперечного сечения, для которой u = 0 на границе трубы, т.е. при
-
Гравитационные волны
Примером нестационарных течений жидкости являются волновые движения с колебаниями отдельных частиц. Рассмотрим волны на поверхности жидкости, возникающие в результате того, что поверхность выведена из состояния равновесия и колеблется под действием силы тяжести. Такие волны называются гравитационными. Гравитационные волны описываются уравнениями нестационарных течений идеальной несжимаемой жидкости.
Пусть начальное возмущение заключается в отклонении жидкости от состояния равновесия. Предположим, что этим начальным возмущением являются мгновенные добавочные давления, вызванные, например, порывом ветра. Возникающие при этом движения будут потенциальны:
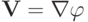 . Уравнение неразрывности обращается в уравнение Лапласа:
. Уравнение неразрывности обращается в уравнение Лапласа: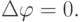
Уравнения движения Эйлера приводятся к интегралу Коши - Лагранжа следующего вида:
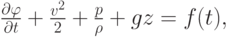
где gz представляет собой потенциал сил тяжести.
Пусть течение медленное, тогда квадратом скорости в последнем уравнении можно пренебречь. Кроме того, так как
 определяется с точностью до произвольной функции, зависящей от времени, то это уравнение можно переписать в виде
определяется с точностью до произвольной функции, зависящей от времени, то это уравнение можно переписать в виде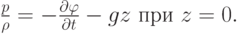
Граничные условия. Предположим, что жидкость ограничена снизу непроницаемой поверхностью. На этой поверхности ставим условие непроницаемости на нормальный компонент скорости:
Свободная поверхность (граница жидкости с газом) будет плоскостью, которую примем за координатную плоскость xy. На свободной поверхности жидкости давление p равно давлению газа над жидкостью (p_0). Граничное условие для скорости на свободной поверхности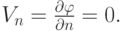
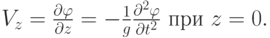
Начальные условия. Пусть возмущенная поверхность в начальный момент (t = 0) определяется уравнением z = f(x, y). Тогда при t = 0, z = 0 справедливо соотношение
Начальные скорости возникают в результате действия импульса давления, равного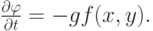
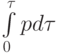 . Потенциал скорости в начальный момент можно представить в виде
. Потенциал скорости в начальный момент можно представить в виде
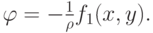
Плоские волны. Рассмотрим волновое движение, называемое плоскими волнами. В этом случае свободная поверхность будет представлять собой илиндрическую поверхность с образующими, параллельными оси y. Пусть жидкость ограничена плоским горизонтальным дном, отстоящим от свободной поверхности на расстояние h. Тогда для искомого потенциала скорости
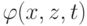 справедливы соотношения
справедливы соотношения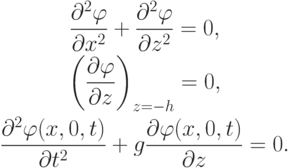
Начальные условия заменим требованием периодичности по времени t и координате x искомого решения.
- Построить аналитическое решение поставленной задачи, представив искомую функцию в виде
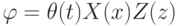 . Показать, что полученное решение — результат наложения четырех колебаний.
. Показать, что полученное решение — результат наложения четырех колебаний. - Получить численное решение и сравнить его с аналитическим.
Определить профиль волны
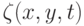 , используя соотношение
, используя соотношение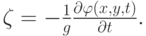
Прогрессивные волны. Провести численное исследование частного случая плоских волновых движений, который определяется потенциалом скорости вида

Профиль волны в этом случае имеет вид
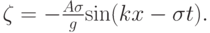
Описать основные закономерности рассматриваемого движения жидкости. Чему равен период волны, частота колебаний? Вывести формулу для траекторий частиц жидкости и сравнить ее на графике с траекторией, получаемой в численном решении.
- Построить аналитическое решение поставленной задачи, представив искомую функцию в виде
