Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1276 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 6:

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

6.2.3. Чебышёвское ускорение метода простых итераций

Рассмотрим итерационный метод с выбором параметра \tau на каждой итерации:

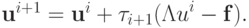
{\mathbf{u}}^{i + 1} = {\mathbf{u}}^{i} + \tau_{i + 1} ({{{\Lambda}u}}^{i} - {\mathbf{f}}).

Соответствующие соотношения для эволюции невязки имеют вид:

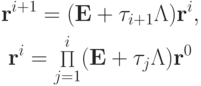
\begin{gather*} {\mathbf{r}}^{i + 1} = ({\mathbf{E}} + \tau_{i + 1}{{{\Lambda}}}){\mathbf{r}}^{i}, \\ {\mathbf{r}}^{i} = {\mathop \Pi\limits_{j = 1}^{i} (\mathbf{E} + \tau_j{\Lambda})}{\mathbf{r}}^0 \end{gather*}

После разложения невязок на двух соседних итерациях по базису из собственных функций сеточного оператора получим равенство

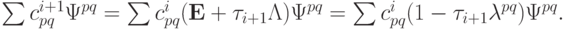
\sum {c_{pq}^{i + 1} {\Psi}^{pq}} = \sum {c^{i}_{pq}(\mathbf{E} + \tau_{i + 1}{ \Lambda}) {\Psi}^{pq}} = \sum {c^{i}_{pq} (1 - \tau_{i + 1} {\lambda}^{pq}) {\Psi}^{pq}}.

Для коэффициентов разложения и компонентов невязки справедливы следующие равенства:

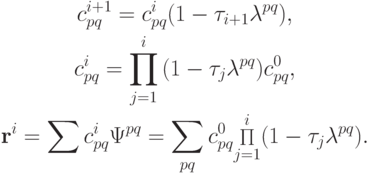
\begin{gather*} c_{pq}^{i + 1} = c_{pq}^{i} (1 - \tau_{i + 1}{\lambda}^{pq}), \\ c_{pq}^{i} = \prod\limits_{j = 1}^{i}{(1 - \tau_j {\lambda}^{pq})} c_{pq}^0, \\ \mathbf{r}^{i} = \sum {c^{i}_{pq} {\Psi}^{pq}} = \sum\limits_{pq}{c^0_{pq}{\mathop \Pi\limits_{j = 1}^{i}(1 - \tau_j {\lambda}^{pq})}}. \end{gather*}

Оценим погрешности на i шаге итераций

\left\| {{\mathbf{r}}^{i}}\right\| \le \max\limits_{{\lambda}\in [l, L]} \left| {\mathop \Pi\limits_{j = 1}^{i} (1 - \tau_j {\lambda}^{pq})}\right| \left\| {\sum {c_{pq} {{\Psi}}^{pq}} }\right\| \le \max\limits_{{\lambda}\in [l, L]} \left| {\mathop \Pi\limits_{j = 1}^{i}(1 - \tau_j {\lambda}^{pq})}\right| \left\| {{\mathbf{r}}^0 }\right\|.

Вновь приходим к минимаксной задаче: найти такую последовательность итерационных параметров 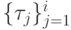\{\tau_j \}_{j = 1}^{i}, чтобы выполнялось

\min\limits_{\{\tau_j \}} \max\limits_{{\lambda}\in [l, L]} \left| {\mathop \Pi\limits_{j = 1}^{i}(1 - \tau_j {\lambda}^{pq})}\right|.

Заметим, что 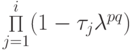{\mathop \Pi\limits_{j = 1}^{i} (1 - \tau_j {\lambda}^{pq})} есть полином (относительно \tau ) степени i. Задача — сделать его наименее уклоняющимся от нуля на отрезке [l, L]. Эта задача, как известно, решена Чебышевым, а корни этого полинома являются нулями полинома Чебышева:

$ \tau_j = \left[{\frac{{L + l}}{2} + \frac{{L - l}}{2} \cos \frac{{{\pi}(2j - 1)}}{{2i}}}\right]^{- 1}, j = 1, 2, \ldots , i. $

Достаточно громоздкие выкладки, которые опускаются, дают в результате оценку скорости сходимости метода с оптимальным набором параметров 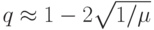q \approx 1 - 2 \sqrt{1/{\mu}}, и числа итераций, необходимого для достижения заданной точности

$ i \approx \left[{\frac{{\sqrt {\mu} }}{2} \ln \cdot {\varepsilon}^{- 1}}\right] + 1. $

Пусть расчеты приводятся с точностью 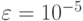\varepsilon = 10^{ - 5} на сетке 100 x 100, тогда оценка числа итераций и скорости сходимости есть 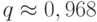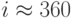q \approx 0, 968, i \approx 360. "Цена" каждой итерации — приблизительно 10 M2 операций.

Однако метод итераций с чебышевскими параметрами в таком виде оказывается неустойчивым по двум причинам: рост ошибок округления в расчетах и некоторые свойства нулей полиномов Чебышева, в частности, сгущение 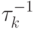\tau_k^{- 1} — величин, обратных корням полинома — к границам спектра. 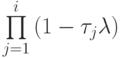Не останавливаясь на доказательстве неустойчивости чебышевского итерационного процесса, заметим, что для ее устранения необходимо переставить итерационные параметры не в их естественном порядке, а так, чтобы все частичные произведения \prod\limits_{j = 1}^{i}{(1 - \tau_j {\lambda})} не возрастали бы вблизи границ спектра при любом i. Эта необходимо, поскольку частичное произведение, относящееся к правой части спектра со сгущающейся чебышевской сеткой, очень быстро растет из - за больших величин 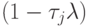(1 - \tau _{j}\lambda ). Задача упорядочения итерационных параметров достаточно сложна, ее решение связано с именами В.И.Лебедева, В.П.Финогенова, А.А.Самарского и Е.С.Николаева [16.4]. Приведем результат ее решения для i = 2r, где i — количество сомножителей в произведении (число итераций) 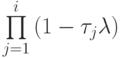\prod\limits_{j = 1}^{i}{(1 - \tau_j {\lambda})}, r — натуральное число.

При i = 2 перебираем корни полинома Чебышева в их естественном порядке (в фигурных скобках указываем номер корня) {1, 2} или в порядке убывания номера {2, 1}. Далее последовательность номеров корней получаем следующим образом. Каждый номер корня меняется на пару чисел: первое число — номер корня, второе — дополняет сумму в каждой паре до значения i + 1(2r + 1). Таким образом, при i = 4 получаем два упорядоченных набора. Из последовательности {1, 2} получаем {1, 4, 2, 3}, а из {2, 1} - {2, 3, 1, 4}. Действуя аналогично далее, имеем при i = 8 {1, 8, 4, 5, 2, 7, 3, 6} в первой последовательности чебышевских параметров или {2, 7, 3, 6, 1, 8, 4, 5} во второй последовательности. Следующий шаг дает i = 16 {1, 16, 8, 9, 4, 13, 5, 12, 2, 15, 7, 10, 3, 14, 6, 11} в первой последовательности чебышевских параметров или {2, 15, 7, 10, 3, 14, 6, 11, 1, 16, 8, 9, 4, 13, 5, 12} - во второй. Построение таких упорядоченных наборов легко можно продолжить. Приведенное упорядочение является универсальным — оно обеспечивает устойчивость любых методов, где необходим чебышевский набор итерационных параметров.

Обычно при реализации чебышевских методов задаются последовательностью из 32 или 64 параметров и делают серию итераций. Если невязка велика, то результат серии используют в качестве начального приближения для следующей серии итераций, если невязка мала, то решение считается найденным. Такая упрощенная реализация работает несколько медленнее, чем "честное" чебышевское ускорение, но весьма эффективно.

Приведем итерационные формулы трехслойного метода Чебышева, который не уступает предыдущему по скорости сходимости, однако не требует изменения порядка выбора итерационных параметров. В качестве платы за удобство использования метода затраты памяти становятся несколько большими. Формулы трехслойного метода будут

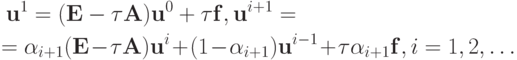
\begin{multline*} {\mathbf{u}}^1 = ({\mathbf{E}} -{\tau}{\mathbf{A}}){\mathbf{u}}^0 + \tau {\mathbf{f}}, {\mathbf{u}}^{{i} + 1} = \\ ={\alpha}_{{i} + 1} ({\mathbf{E}} - \tau {\mathbf{A}}){\mathbf{u}}^{i} + (1 -{\alpha}_{{i} + 1}){\mathbf{u}}^{{i} - 1} +{\tau}\alpha_{{i} + 1}{\mathbf{f}}, i = 1, 2, \ldots \end{multline*}

где 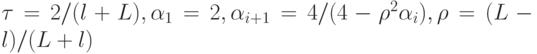{\tau} = 2/(l + L),{\alpha}_1 = 2,{\alpha}_{{i} + 1} = 4/(4 - {\rho}^2 {\alpha}_i ), {\rho} = (L - l)/(L + l).

Можно показать, что погрешность ri удовлетворяет оценке

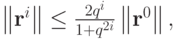
$ \left\| {{\mathbf{r}}^{i}}\right\| \le \frac{{2q^{i}}}{{1 + q^{2{i}}}} \left\| {{\mathbf{r}}^0 }\right\|, $

где

$ q = \frac{1 - 1/\sqrt{{\mu}}}{1 + 1/\sqrt{{\mu}}}. $

Трехслойный метод Чебышева можно также представить в следующем виде:

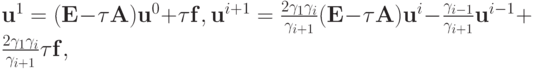
$ {\mathbf{u}}^1 = ({\mathbf{E}} -{\tau}{\mathbf{A}}){\mathbf{u}}^0 + \tau {\mathbf{f}}, {\mathbf{u}}^{{i} + 1} = \frac{{2 \gamma_1 \gamma_i }}{{\gamma_{{i} + 1}}}({\mathbf{E}} -{\tau}{\mathbf{A}}){\mathbf{u}}^{i} - \frac{{\gamma_{{i} - 1}}}{{\gamma_{{i} + 1}}}{\mathbf{u}}^{{i} - 1} + \frac{{2 \gamma_1 \gamma_i }}{{\gamma_{{i} + 1}}}{\tau}{\mathbf{f}}, $

где

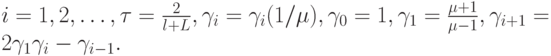
$ {i} = 1, 2, \ldots ,{\tau} = \frac{2}{{l + L}}, \gamma_i = \gamma_i ({1/{\mu}}), \gamma_0 = 1, \gamma_1 = \frac{{\mu}+ 1}{{\mu}- 1}, \gamma_{{i} + 1} = 2 \gamma_1 \gamma_i - \gamma_{{i} - 1} . $

Трехслойный метод Чебышева в настоящее время применяется значительно чаще двухслойного при численном решении уравнений эллиптического типа.

Каноническая форма записи трехслойного итерационного метода (к которым и относится приведенный трехслойный метод Чебышева) есть

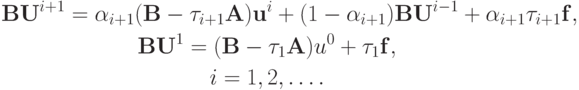
\begin{gather*} {\mathbf{BU}}^{{i} + 1} ={\alpha}_{{i} + 1}({\mathbf{B}} - \tau_{{i} + 1}{\mathbf{A}}) {\mathbf{u}}^{i} + (1 -{\alpha}_{{i} + 1}){\mathbf{BU}}^{{i} - 1} + {\alpha}_{{i} + 1} \tau_{{i} + 1}{\mathbf{f}}, \\ {\mathbf{BU}}^1 = ({\mathbf{B}} - \tau_1 {\mathbf{A}})u^0 + \tau_1 {\mathbf{f}}, \\ {i} = 1, 2, \ldots . \end{gather*}

Если оператор 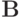\mathbf{B} — единичный, то трехслойный итерационный метод называется явным, в противном случае — неявным. Заметим, что каноническая форма записи двухслойного итерационного метода имеет вид

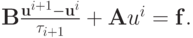
$ {\mathbf{B}} \frac{{{\mathbf{u}}^{{i} + 1} - {\mathbf{u}}^{i}}}{{\tau_{{i} + 1}}} + {\mathbf{A}}u^{i} = {\mathbf{f}}. $

Если оператор 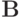\mathbf{B} — единичный, то двухслойный итерационный метод называется явным, в противном случае — неявным.

Каноническая форма записи трехслойного итерационного метода получается из двухэтапного итерационного процесса. На первом этапе (предиктор) используется метод

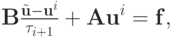
$ {\mathbf{B}} \frac{{\tilde{\mathbf{u}} - {\mathbf{u}}^{i} }}{{\tau_{{i} + 1}}} + {\mathbf{Au}}^{i} = {\mathbf{f}}, $

где $ \tilde{\mathbf{u}} $ — промежуточное значение. Второй этап — корректор:

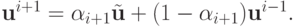
{\mathbf{u}}^{{i} + 1} ={\alpha}_{{i} + 1} \tilde{\mathbf{u}} + (1 -{\alpha}_{{i} + 1}){\mathbf{u}}^{{i} - 1}.

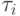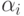В трехслойных схемах используются два итерационных параметра: \tau _{i} и {\alpha}_i причем при 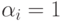{\alpha}_i = 1 трехслойная схема переходит в двухслойную. Рассмотренные методы основываются на следующих свойствах оператора \mathbf{A}:

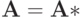  • самосопряженность: {\mathbf{A}} = {\mathbf{A}}*,
  • положительная определенность: {\mathbf{A}} > 0, 0 < l < \lambda_i < L ; для реализации алгоритма необходимо знание только границ спектра оператора.
Дальше >>
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

Вопросы и ответы

вопросов: 0