НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 3: Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.8. Идеи построения сеточно - характеристических методов и анализ разностных схем в пространстве неопределенных коэффициентов

Идея построения метода.

Продемонстрируем основные идеи построения сеточно - характеристических методов на примере решения простейшего линейного уравнения переноса:

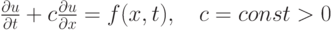${\frac{{\partial}u}{{\partial}t} + c \frac{{\partial}u} {{\partial}x} = f(x, t), \quad c = {const} > 0}$

( 3.12)

с соответствующими начальными и граничными условиями.

Известно, что (3.12) имеет характеристику, определяемую уравнением характеристики:

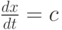
$\frac{dx}{dt} = c$

и вдоль нее превращается в обыкновенное дифференциальное уравнение (ОДУ):

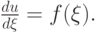
$\frac{du}{d \xi} = f(\xi ).$

Рис. 3.1.

В частности, для однородного уравнения (1) значение функции u вдоль характеристики не меняется. На сведении уравнения в частных производных к ОДУ построены так называемые методы характеристик.

Методы сеток основаны на введении в области интегрирования уравнения разностной сетки, сеточного шаблона, т.е. совокупности узлов сетки, используемых для замены дифференциального уравнения (в малой области) разностным аналогом (аппроксимацией). При анализе аппроксимации обычно используются разложения проекции на сетку точного решения дифференциальной задачи в ряд Тейлора.

Рассмотрим класс методов, в которых одновременно использован и сеточный, и характеристический подход.

В области интегрирования введем разностную сетку:

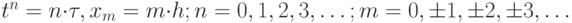
$t^{n} = {n} \cdot{\tau}, x_m = {m} \cdot h; {n} = 0, 1, 2, 3, \ldots; {m} = 0, ±1, ±2, ±3, \ldots$

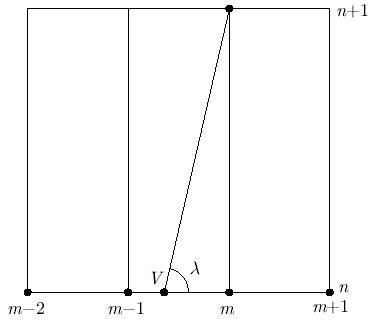
Значение решения (1) в узлах сетки обозначим через 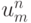$u_m^{n}$ . Для перехода на следующий временной шаг сетки будем использовать явный пятиточечный шаблон (рис. 3.1). Необходимо вычислить значение 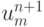$u_m^{n + 1}$ , используя значения u на n слое по времени. Проведем из точки { n + 1, m } характеристику с наклоном $\lambda$ до пересечения со слоем tⁿ в точке V. 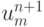Тогда вдоль характеристики значение $u_m^{n + 1}$ выражается через 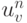$u_{v}^{n}$ , например, как

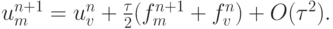${u_m^{n + 1} = u_{v}^{n} + \frac{\tau}{2} (f_m^{n + 1} + f_{v}^{n}) + O({\tau}^2).}$

( 3.13)

Выражение (3.13) получено, как аппроксимация обыкновенного дифференциального уравнения вдоль характеристики методом трапеций. Проводя ту или иную интерполяцию для нахождения значения 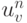$u_{v}^{n}$ по точкам слоя tⁿ, получим различные разностные схемы для определения 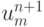$u_m^{n + 1}$ на данном шаблоне.

О физическом смысле условия Куранта.

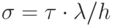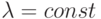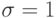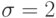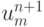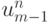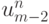Пусть ${\sigma}={\tau} \cdot {\lambda}/h$ — число Куранта. В случае $\lambda = const$ очевидно, что выбором $\tau$ и h можно добиться $\sigma = 1$ или $\sigma = 2$ . В этом случае характеристика, проведенная через точку $u_m^{n + 1}$ , попадет в узел разностной сетки, где значение $u_{m - 1}^{n}$ (или $u_{m - 2}^{n}$ соответственно) известно точно. Для однородного уравнения происходит перенос значения в точку 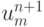$u_m^{n + 1}$ вдоль характеристики. Если 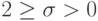$2 \ge \sigma > 0$ , то для определения значения 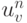$u_{v}^{n}$ приходится решать задачу интерполяции, а для $\sigma > 2$ — задачу экстраполяции по узлам сетки. Известно, что вторая задача, как правило, неустойчива.

Точку V назовем областью влияния дифференциального уравнения (1), а точки шаблона, по которым проводится интерполяция — областью влияния разностного уравнения. Для устойчивости разностной схемы необходимо, чтобы область влияния дифференциальной задачи лежала внутри области влияния разностной — это проявление условия КФЛ.

Пространство неопределенных коэффициентов.

Запишем разностную схему в виде

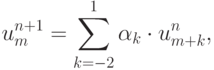${u_m^{n + 1} = \sum\limits_{k = - 2}^1 {\alpha_k \cdot u_{{m} + k}^{n}}, }$

( 3.14)

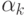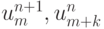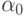где коэффициенты ${\alpha}_k$ будем искать из условий аппроксимации, раскладывая $u_m^{n + 1}, u_{m + k}^{n}$ в ряды Тейлора в окрестности точки ( tⁿ, x_m ). Оставляя свободными два коэффициента (например, ${\alpha}_{- 2}$ , ${\alpha}_0$ ), получаем условия аппроксимации порядка $O(\tau + h)$ :

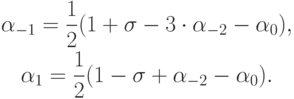
$\begin{gather*} {\alpha}_{- 1} = \frac{1}{2}(1 + {\sigma}- 3 \cdot {\alpha}_{- 2} -{\alpha}_0 ), \\ {\alpha}_1 = \frac{1}{2}(1 - {\sigma}+{\alpha}_{- 2} -{\alpha}_0 ). \end{gather*}$

Примем свободные коэффициенты за координатные оси линейного пространства с евклидовой метрикой. Каждая точка этого пространства будет соответствовать разностной схеме первого порядка аппроксимации. Кроме того, можно выделить множество схем порядка 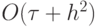$O(\tau + h^{2})$

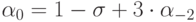${\alpha_0 = 1 - {\sigma}+ 3 \cdot{\alpha}_{- 2}}$

( 3.15)

Дальше >>

Авторизоваться

Численные методы решения уравнений в частных производных

Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)

3.8. Идеи построения сеточно - характеристических методов и анализ разностных схем в пространстве неопределенных коэффициентов

Вопросы и ответы