НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 3: Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1276 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Исследовать на спектральную устойчивость разностную схему на шаблоне квадрат
$\begin{gather*} \frac{1}{{2{\tau}}} \left[{(u_{m + 1}^{n + 1} + u_m^{n + 1}) - (u_{m + 1}^{n} - u_m^{n})}\right] + \\ + \frac{1}{h} \left[{(u_{m + 1}^{n + 1} + u_{m + 1}^{n}) - (u_m^{n + 1} - u_m^{n})}\right] = f_{m + 1/2}^{n + 1/2}, \end{gather*}$

аппроксимирующую линейное уравнение переноса

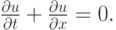
$\frac{{\partial}u}{{\partial}t} + \frac{{\partial}u} {{\partial}x} = 0.$

Решение. После подстановки в схему гармоник Фурье

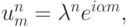
$u_m^{n} = {\lambda}^{n} e^{i{\alpha} m},$
получим выражение для спектра оператора послойного перехода

${\lambda}(\alpha ) = \frac{1 - i{\sigma}{\tg{\alpha}/2}}{1 + i{\sigma}{\tg{\alpha}/2}}, {\sigma}={\tau}/h \mbox{ - число Куранта.}$

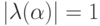Тогда $\left| {{\lambda}(\alpha )}\right| = 1$ и рассматриваемая схема безусловно устойчива. Этого следовало ожидать, так как аппроксимация производной по времени производится как на нижнем, так и на верхнем временном слое. Однако решение на верхнем слое выписывается в явном виде, поскольку правое условие ставится на левой границе. Поэтому схему иногда относят к явным схемам бегущего счета. Расчетная формула будет

$u_{m + 1}^{n + 1} = u_m^{n} + \frac{{{\sigma}- 1}}{{{\sigma}+ 1}}(u_m^{n + 1} - u_{m + 1}^{n}) + {\tau}f_{m + 1/2}^{n + 1/2} .$

Схема обладает вторым порядком аппроксимации по времени и пространственной координате.
Получить дисперсионное соотношение для разностных схем первого и второго порядка сходимости для аппроксимации нелинейного уравнения
$\frac{{\partial}v}{{\partial}t} + u \frac{{\partial}v}{{\partial}x} = 0, \quad \mbox{где} \quad u \ne {const},$

и, вообще говоря, зависит от решения.

Указание. Использовать дисперсионное соотношение для данного дифференциального уравнения в виде 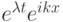$e^{\lambda t} e^{ikx}$ , где k — волновое число, $\lambda = - uki$ .

Решение. Будем искать дисперсионное соотношение для разностного уравнения в виде

$v_m^{n} = e^{{\lambda}(k)t_n } \cdot e^{{ikx}_m } = e^{{\lambda}n{\tau}+ {ikmh}}.$
После его подстановки в схему правый уголок первого порядка аппроксимации, получим

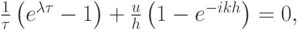
$\frac{1}{\tau} \left({e^{{\lambda}{\tau}} - 1}\right) + \frac{u}{h} \left({1 - e^{- {ikh}}}\right) = 0,$

откуда следует

${\lambda}\left({{\tau}, h, k}\right) ={\tau}^{- 1} \ln \left\{{1 - \frac{u \tau}{h} + \frac{u \tau}{h}e^{- ikh}}\right\}.$

Сравним дисперсионное соотношение для дифференциального и соответствующих разностных уравнений.

Пусть
$\frac{{u{\tau}}}{h} = 1.$
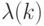Имеет место совпадение $\lambda (k)$ и $\lambda (\tau , h, k)$ , однако этот случай мало интересен для вычислительной практики, поскольку u может меняться в ходе решения задачи. Для проведения дисперсионного анализа схем положим $kh \ll 1$ , имея в виду то, что h — малый параметр, а аппроксимация тем лучше, чем меньше волновое число, т.е. чем более гладким является исследуемое частное решение. Заметим, что для расчетной сетки с шагом h обычно реализуются волновые числа $k \approx 2 \pi h^{- 1}$ .

В таком случае дисперсионное соотношение будет

$\begin{gather*} {\lambda}\left({{\tau}, {h, k}}\right) \approx - {iuk} - \frac{{{uhk}^2}}{2} \left({1 - \frac{{u{\tau}}}{h}}\right) = {\lambda}(k) - \frac{{k^2}}{2}{uh} \left({1 - {\sigma}}\right), \\ {\sigma}= u{\tau}/h \mbox{ - число Куранта, } \end{gather*}$

а частное решение примет вид

$\exp (ik({mh} - {un}{\tau})) \cdot \exp \left({- \frac{1}{2}{uk}^2 (h - u{\tau})n{\tau}}\right).$

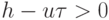Первый сомножитель совпадает с соответствующим частным решением дифференциального уравнения, второй является особенностью разностного решения; его поведение при различных $\tau , h, k$ представляет особенный интерес. При u < 0, $h - u\tau > 0$ , как видно из этого решения, рассматриваемую схему нельзя использовать для проведения расчетов. Второй сомножитель имеет порядок exp (k² | u | ht_n), он быстро растет при 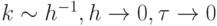$k \sim h^{- 1}, h \to 0,{\tau}\to 0$ . 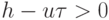Аналогичная ситуация получается и при u > 0, $h - u\tau < 0$ . При u < 0, $h - u\tau > 0$ второй сомножитель затухает с ростом t_n тем быстрее, чем больше k, или чем меньше 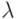$\lambda$ — длина волны частного решения вида exp(ikx). Таким образом, численное решение, полученное по схеме уголок, отличается от точного, в котором все гармоники сохраняют амплитуду с ростом t_n, наличием затухающего множителя для гармоник с большими волновыми числами (или малыми длинами волн). Действие этого сомножителя приводит к сглаживанию решений, имеющих разрыв в начальных данных.

Для разностной схемы Лакса - Вендроффа второго порядка

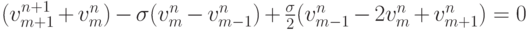
$(v_{m + 1}^{n + 1} + v_m^{n}) - \sigma (v_m^{n} - v_{m - 1}^{n}) + \frac{{\sigma}}{2} (v_{m - 1}^{n} - 2v_m^{n} + v_{m + 1}^{n}) = 0$

дисперсионное соотношение будет

${\lambda} ={\tau}^{- 1} \ln \left\{{1 + {\sigma}(e^{- {ikh}} - 1) + {2uh}(1 - \sigma) {\rm sin}}^2 \frac{{kh}}{2}\right\},$

для длинноволновых гармоник с $kh \ll {1}$

${\lambda}\left({{\tau}, {h, k}}\right) \approx - {iku} + i \frac{{k^3 u}}{6} (h^2 - u^2{\tau}^2 ) = {\lambda}(k) + ik^3 \frac{{{uh}^2}}{6} (1 - {\sigma}^2 ).$

Из полученных соотношений можно сделать следующий вывод. Решения исходного уравнения переноса имеют вид волн с волновым числом k, которые движутся вправо со скоростью u, так как

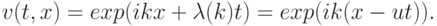
$v(t, x) = exp(ikx + \lambda (k)t) = exp(ik(x - ut)).$

Решения разностного уравнения имеют вид

$\begin{gather*} v \left({t_n , x_m }\right) = \exp ({ikx}_m + {\lambda}({\tau}, {h, k})t_n ) = \\ = \exp \left({ik \left\{{x_m - u \left[{1 - \frac{{k^2}}{6} \left({h^2 - u^2{\tau}^2}\right)} \right]t_n }\right\}}\right) = \\ = \exp \left({ik \left\{{x_m - u \left[{1 + {U}_k (k)}\right]t_n }\right\}}\right), \end{gather*}$

где введено обозначение

$U_k = - \frac{k^2}{6} \left({h^2 - u^2{\tau}^2}\right).$

Последнее выражение означает, что разностные решения уже не имеют вид волн, движущихся с одной и той же скоростью. Теперь каждая волна со своей частотой движется с собственной скоростью u = U_k[1 + u(k)]. Разумеется, при малых k и скорости u_k мало отличаются от u, но высокочастотные волны движутся со скоростями, заметно отличающимися от скорости переноса. Кроме того, в схеме Лакса - Вендроффа гармоники со временем не затухают, численное решение не сглаживается со временем. Начальный волновой пакет u и определенный им начальный профиль решения, изменяются с течением времени из - за рассогласования фаз. Это приводит к потере монотонности профиля v(x), если он был вначале монотонным, и появлению осцилляций разностного происхождения. Появление сеточной дисперсии — одно из проявлений эффекта Гиббса, подробнее об эффекте Гиббса в [13.16].
Акустическая система описывает распространение плоских звуковых волн. Поставим для нее задачу Коши:
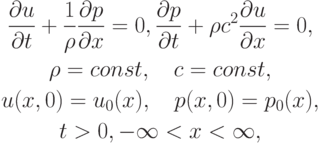
$\begin{gather*} \frac{{\partial}u}{{\partial}t} + \frac{1}{\rho} \frac{{\partial}p}{{\partial}x} = 0, \frac{{\partial}p}{{\partial}t} + {\rho}c^2 \frac{{\partial}u}{{\partial}x} = 0, \\ {\rho} = {const}, \quad c = {const}, \\ u(x, 0) = u_0 (x), \quad p(x, 0) = p_0 (x), \\ t > 0, - \infty < x < \infty , \end{gather*}$

где u — скорость движения среды, p — давление, 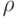$\rho$ - плотность среды, c — скорость звука в среде.
- a) Представить акустическую систему в интегральной форме.
- b) Преобразовать акустическую систему к виду системы с разделенными переменными.
- c) Предложить разностную схему первого порядка точности для ее решения.
Решение.
- a) Проинтегрировав акустическую систему по произвольной области с границей G, получим:
  $\begin{gather*} \oint\limits_{\Gamma}{{\rho}udx - {pdt}} = 0, \\ \oint\limits_{\Gamma}{\frac{p}{c^2}dx - {\rho}{udt}} = 0. \end{gather*}$
- b) Умножим второе уравнение на $(\rho c)^{ - 1}$ , затем сложим с первым и вычтем из него. Получим систему двух уравнений
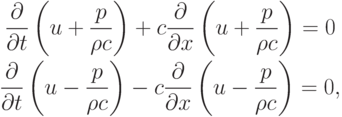
  $\begin{gather*} \frac{{\partial}}{{\partial}t} \left({u + \frac{p}{{\rho}c}}\right) + c \frac{{\partial}}{{\partial}x} \left({u + \frac{p}{{\rho}c}}\right) = 0 \\ \frac{{\partial}}{{\partial}t} \left({u - \frac{p}{{\rho}c}}\right) - c \frac{{\partial}}{{\partial}x} \left({u - \frac{p}{{\rho}c}}\right) = 0, \end{gather*} $$
  
  или, после введения обозначений (инвариантов Римана)
  $R = u + \frac{p}{{\rho}c}, S = u - \frac{p}{{\rho}c}$
  система запишется в виде двух уравнений переноса:
  
  $\frac{{{\partial}R}}{{\partial}t} + c \frac{{{\partial}R}}{{\partial}x} = 0 \quad \frac{{{\partial}S}}{{\partial}t} - c \frac{{{\partial}S}}{{\partial}x} = 0.$
Эта система позволяет выписать общее решение:
```
R = f(x - ct),  S = g(x + ct).
```
Здесь f, g — произвольные непрерывно дифференцируемые функции, определяемые из начальных условий. В терминах инвариантов Римана можно определить и значения естественных переменных u, p:

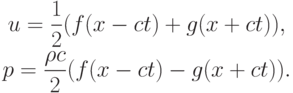
$\begin{gather*} u = \frac{1}{2}(f(x - ct) + g(x + ct)), \\ p = \frac{{\rho}c}{2}(f(x - ct) - g(x + ct)). \end{gather*}$

Замечательное свойство инвариантов Римана R, S заключается в их постоянстве вдоль прямых x - ct = const, и x + ct = const или
$\frac{dx}{dt} = \pm c$
— характеристик акустической системы.

Если задавать начальные данные 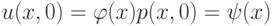$u(x, 0) = {\varphi}(x) p(x, 0) = {\psi}(x)$ , ${- \infty < x < \infty}$ , то связь начальных данных и инвариантов Римана будет

${\varphi}\left(x\right) = \frac{1}{2}(f(x) + g(x)), {\psi}(x) = \frac{{\rho}c}{2} \left[{f(x) - g(x)}\right],$

откуда получим

$f(x) = {\varphi}(x) + \frac{{{\psi}(x)}}{{\rho}c}, g(x) = {\varphi}(x) - \frac{{{\psi}(x)}}{{\rho c}}.$

Следовательно, решение системы в этом случае

$\begin{gather*} u(t, x) = \frac{1}{2}({\varphi}(x - ct) + {\varphi}(x + ct)) + \frac{1}{{2 {\rho}c}}({\psi}(x - ct) + {\psi}(x + ct)), \\ p(t, x) = \frac{1}{2}({\varphi}(x - ct) + {\varphi}(x + ct)) - \frac{{\rho}c}{2}({\psi}(x - ct) + {\psi}(x + ct)). \end{gather*}$

Для численного решения системы, записанной в инвариантах Римана, можно применить схему Куранта - Изаксона - Риса:

$\begin{gather*} \frac{{R_m^{n + 1} - R_m^{n}}}{\tau} + c \frac{{R_m^{n + 1} - R_{m - 1}^{n}}}{h} = 0, \\ \frac{{S_m^{n + 1} - S_m^{n}}}{\tau} - c \frac{{S_{m + 1}^{n} - S_m^{n}}}{h} = 0, \end{gather*}$

или

$\begin{gather*} R_m^{n + 1} = \left({1 - {\sigma}}\right)R_m^{n} + {\sigma}R_{m - 1}^{n}, \\ S_m^{n + 1} = \left({1 + {\sigma}}\right)S_m^{n} - {\sigma}S_{m + 1}^{n} . \end{gather*}$

Известно, что данная схема имеет первый порядок аппроксимации и является устойчивой при выполнении условия КФЛ:
$\frac{{c{\tau}}}{h} \le 1.$
Заменить смешанную задачу для волнового уравнения
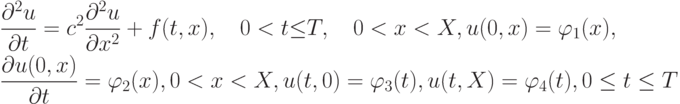
$\begin{gather*} \frac{{{\partial}^2 u}}{{\partial}t} = c^2 \frac{{{\partial}^2 u}}{{{\partial}x^2}} + f(t, x), \quad 0 < t {\le} T, \quad 0 < x < X, u(0, x) = \varphi_1 (x), \\ \frac{{{\partial}u(0, x)}}{{\partial}t} = \varphi_2 (x), 0 < x < X, u(t, 0) = \varphi_3 (t), u(t, X) = \varphi_4 (t), 0 \le t \le T \end{gather*}$

эквивалентной ему парой уравнений в частных производных первого порядка.

Решение. Введем новые переменные

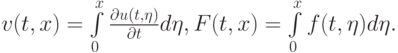
$v(t, x) = \int\limits_0^{x}{\frac{{{\partial}u(t, \eta )}}{{\partial}t}d \eta }, F(t, x) = \int\limits_0^{x}{f(t, \eta )d \eta } .$

Функции u(t, x), v(t, x), что несложно проверить, удовлетворяют акустической системе уравнений

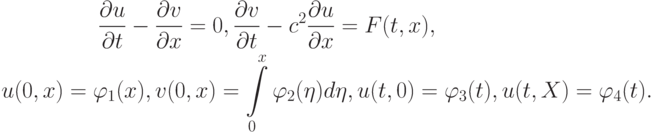
$\begin{gather*} \frac{{\partial}u}{{\partial}t} - \frac{{\partial}v} {{\partial}x} = 0, \frac{{\partial}v}{{\partial}t} - c^2 \frac{{\partial}u}{{\partial}x} = F(t, x), \\ u(0, x) = \varphi_1 (x), v(0, x) = \int\limits_0^{x}{\varphi_2} (\eta )d \eta , u(t, 0) = \varphi_3 (t), u({t, X}) = \varphi_4 (t). \end{gather*}$

Введем в рассмотрение параметрическую схему для численного решения этой системы:

$\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \frac{{c^2}}{h} \left\{{\xi_1 (v_{m + 1}^{n + 1} - v_m^{n + 1}) + (1 - \xi_1 )(v_{m + 1}^{n} - v_m^{n})}\right\} + F_{m + 1/2}^{n + 1/2}, \\ \frac{{v_m^{n + 1} - v_m^{n}}}{\tau} = \frac{1}{h} \left\{{\xi_2 (u_m^{n + 1} - u_{m - 1}^{n + 1}) + (1 - \xi_2 )(u_m^{n} - u_{m - 1}^{n})}\right\}, \\ 0 \le \xi_1 , \xi_2 \le 1. \end{gather*}$

Исследование полученной двухпараметрической разностной схемы на спектральную устойчивость дает условия устойчивости:
$\xi_1 + \xi_2 \ge 1, {\sigma}^2 \left({2 \xi_1 - 1}\right) \left({2 \xi_2 - 1}\right) \ge - 1, {\sigma}= \frac{{c \tau }}{h}.$
Отсюда видно, что если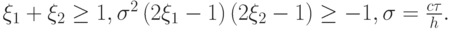 $\xi_1 \ge 0, 5$ и ${\xi}_2 \ge 0, 5$ , то схема устойчива при любых числах Куранта и сеточных параметрах, если $\xi_1 + {\xi}_2 \ge 1$ , но один из параметров меньше 0, 5, то схема условно устойчива при
${\tau}\le \frac{h}{c}(2 \xi_1 - 1)^{- 1} (2 \xi_2 - 1)^{- 1}.$

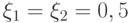Пусть $\xi _{1} = \xi _{2} = 0, 5$ . Тогда полученная схема является безусловно устойчивой и обладает вторым порядком аппроксимации по обоим переменным.
Исследовать на сходимость схему "крест" с шаблоном

для численного решения волнового уравнения
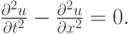
$\frac{{\partial}^2 u}{{\partial}t^2} - \frac{{\partial}^2 u}{{\partial}x^2} = 0.$

Решение. Запишем разностную схему:

${\mathbf{L}}_{\tau} u_{\tau} = \frac{{u_m^{n + 1} - 2u_m^{n} + u_m^{n - 1}}}{{{\tau}^2}} - \frac{{u_{m - 1}^{n} - 2u_m^{n} + {u}_{m + 1}^{n}}}{{h^2}} = 0.$

Исследование на аппроксимацию дает выражение для главного члена невязки

$r_{\tau} = \frac{{{\tau}^2}}{{12}}u_t^{(4)} - \frac{{h^2}}{{12}} u_x^{(4)} + O({\tau}^2 , h^2 ).$

Схема имеет второй порядок аппроксимации. Исследуем схему на устойчивость по спектральному признаку. Для спектра оператора послойного перехода получается

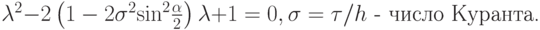
${\lambda}^2 - 2 \left({1 - 2 {\sigma}^2 {\sin}^2 \frac{\alpha }{2}} \right) {\lambda}+ 1 = 0, {\sigma}={\tau}/h \mbox{ - число Куранта.}$

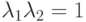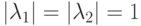По теореме Виета, произведение корней $\lambda _{1} \lambda _{2} = 1$ , и условие устойчивости выполняется, если $| \lambda _{1} | = | \lambda _{2} | = 1$ . Для полученного квадратного уравнения с действительными коэффициентами это означает, что его корни являются комплексно сопряженными. Это возможно лишь в случае, если дискриминант

$D(\alpha ) = 4 {\sigma}^2 {\sin}^2{\alpha} \left({{\sigma}^2 {\sin}^2 \frac{\alpha }{2} - 1}\right)$

будет отрицательным. Условие устойчивости будет выполнено для всех гармоник, если $\sigma < 1$ .