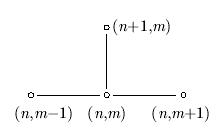Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 3:

Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

Приведем разностные уравнения для схемы Лакса во внутренних точках расчетной области:

$ \frac{{u_m^{n + 1} - 0, 5(u_{m + 1}^{n} + u_{m - 1}^{n})}}{\tau} + c \frac{{u_{m + 1}^{n} - u_{m - 1}^{n}}}{2h} = 0. $

На рисунке приведен шаблон для схемы Лакса. Напомним, что шаблоном разностной схемы называется конфигурация узлов, значения сеточной функции в которых определяют вид разностных уравнений во внутренних (не приграничных) точках сетки. Как правило, на рисунках с изображениями шаблонов точки, участвующие в вычислении производных, соединяются линиями.

Схема Куранта - Изаксона - Риса (КИР), которую иногда также связывают с именем С.К. Годунова, получается при 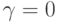\gamma = 0, q = \sigma\ sign\ c. Ее порядок аппроксимации O(\tau + h). Схема КИР условно устойчива, т.е. при выполнении условия Куранта {\sigma}= c{\tau}/h \le 1. Приведем разностные уравнения для схемы Куранта - Изаксона - Риса во внутренних точках расчетной области:

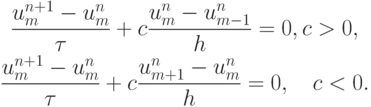
\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} = 0, c > 0, \\ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_{m + 1}^{n} - u_m^{n}}}{h} = 0, \quad c < 0. \end{gather*}

Эти схемы, имеющие также название схемы с разностями против потока (в англоязычной литературе — upwind) могут быть записаны в виде

u_m^{n + 1} = u_m^{n} - {\sigma}\left\{ \begin{array}{cc} u_{m + 1}^{n} - u_m^{n}, & a < 0, \\ u_m^{n} - u_{m - 1}^{n}, & a \ge 0. \\ \end{array} \right.

Их преимущество состоит в более точном учете области зависимости решения. Если ввести обозначения

$ a^{+} = \frac{1}{2}(a + \left|{a}\right|) = \left\{ \begin{array}{cc} a, & a \ge 0, \\ 0, & a < 0, \\ \end{array} \right. a^{-} = \frac{1}{2}(a - \left|{a}\right|) = \left\{ \begin{array}{cc} 0, & a \ge 0, \\ a, & a < 0, \\ \end{array} \right. $

то обе схемы можно записать в следующих формах:

\begin{gather*} u_m^{n + 1} = u_m^{n} - \frac{\tau}{h} \left[{a^{+} (u_m^{n} - u_{m - 1}^{n}) + a^{-} (u_{m + 1}^{n} - u_m^{n})}\right]; \\ u_m^{n + 1} = u_m^{n} - \frac{\tau}{h}(f_{m + 1/2}^{n} - f_{m - 1/2}^{n}), \quad f_{m + 1/2}^{n} = \\ = \frac{1}{2} \left[{a(u_{m + 1}^{n} + u_m^{n}) - \left| a\right|(u_{m + 1}^{n} - u_m^{n})}\right], \\ f_{m - 1/2}^{n} = \frac{1}{2} \left[{a(u_m^{n} + u_{m - 1}^{n}) - \left| a\right|(u_m^{n} - u_{m - 1}^{n})}\right] \end{gather*}

(потоковая форма разностного уравнения);

$ u_m^{n + 1} = u_m^{n} - \frac{1}{2} \sigma (u_{m + 1}^{n} - u_{m - 1}^{n}) + \frac{{\left| \sigma\right|}}{2}(u_{m + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n}) $

(здесь явно выделен член со второй разностью, придающий устойчивость схеме);

$ \Delta_{\tau} u_m^{n} = \frac{{\left| \sigma\right| - {\sigma}}}{2} {\Delta}^{+} u_m^{n} - \frac{{\left| \sigma\right| + {\sigma}}}{2} {\Delta}^{-} u_m^{n} $

(уравнение в конечных приращениях).

Рассмотрим также метод неопределенных коэффициентов для построения разностной схемы правый уголок первого порядка точности для уравнения переноса

$ \frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x} = {\varphi}(t, x), \mbox{ т.е. при } a = - 1. $

Схему можно представить в виде

\begin{gather*} L_{\tau} u^{\tau} = b_1 u_m^{n + 1} + b_2 u_m^{n} + b_3 u_{{m} + 1}^{n} = \varphi_m^{n}, \\ b_1 ={\tau}^{- 1}, b_2 = h^{- 1} -{\tau}^{- 1}, b_3 = - h^{- 1} . \end{gather*}

Схема Куранта - Изаксона - Риса тесно связана с численными методами характеристик. Дадим краткое описание идеи таких методов.

Две последние полученные схемы (при разных знаках скорости переноса) можно интерпретировать следующим образом. Построим характеристику, проходящую через узел ( tn + 1, xm ), значение в котором необходимо определить, и пересекающую слой tn в точке x' = x_{m} - c \tau. Для определенности считаем, что скорость переноса c положительна.

Проведя линейную интерполяцию между узлами xm - 1 и xm на нижнем слое по времени, получим

\begin{gather*} u_m (x^{\prime}) = u_{m - 1} \frac{{x_m - x^{\prime}}}{h} + u_m \frac{{x^{\prime} - x_{m - 1}}}{h} = \\ = \frac{{c{\tau}}}{h}u_{m - 1} + (1 - \frac{{c{\tau}}}{h})u_m = {\sigma}u_{m - 1} - (1 - {\sigma})u_m . \end{gather*}

Далее перенесем вдоль характеристики значение un(x') без изменения на верхний слой tn + 1, т.е. положим u_m^{n + 1} = u_n (x^{\prime}). Последнее значение естественно считать приближенным решением однородного уравнения переноса. В таком случае

u_m^{n + 1} = (1 - {\sigma})u_m + {\sigma}u_{m - 1},

или, переходя от числа Куранта снова к сеточным параметрам,

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + a \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} = 0, $

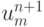т.е. другим способом пришли к уже известной схеме "левый уголок", устойчивой при {\sigma} = c{\tau}/h \le 1, \quad c > 0. При \sigma > 1 точка пересечения характеристики, выходящей из узла ( tn + 1, xm, с n - м слоем по времени расположена левее узла ( tn, xm - 1 ). Таким образом, для отыскания решения u_m^{n + 1} используется уже не интерполяция, а экстраполяция, которая оказывается неустойчивой.

Неустойчивость схемы "правый уголок" при c > 0 также очевидна. Для доказательства этого можно использовать либо спектральный признак, либо условие Куранта, Фридрихса и Леви. Аналогичные рассуждения можно провести и для случая c < 0 и схемы "правый уголок".


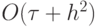Неустойчивая четырехточечная схема получается при \gamma = 0,\ q = 1, ее порядок аппроксимации O(\tau + h^{2}). Сеточные уравнения для разностной схемы будут иметь следующий вид:

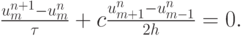
$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_{{m} + 1}^{n} - u_{m - 1}^{n}}}{2h} = 0. $

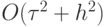Схема Лакса - Вендроффа возникает при \gamma = 0,\ q = \sigma^2. Порядок аппроксимации схемы Лакса - Вендроффа есть O(\tau ^{2} + h^{2}). Схема устойчива при выполнении условия Куранта {\sigma}= c{\tau}/h \le 1.

Эту схему можно получить либо методом неопределенных коэффициентов, либо путем более точного учета главного члена погрешности аппроксимации. Рассмотрим процесс вывода схемы Лакса - Вендроффа подробнее. Проводя исследование предыдущей четырехточечной схемы на аппроксимацию (а исследование это довольно элементарно и сводится к разложению функции проекции на сетку точного решения дифференциальной задачи в ряд Тейлора), получим для главного члена погрешности

\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_{{m} + 1}^{n} - u_{m - 1}^{n}}}{2h} = \left. {\frac{{\partial}u}{{\partial}t} + c \frac{{\partial}u}{{\partial}x}} \right|_{t_n , x_m } + \\ + c^2 \frac{\tau}{2} \frac{{{\partial}^2 u}}{{{\partial}x^2}} + O({\tau}^2 + h^2 ). \end{gather*}

При выводе выражения для главного члена погрешности аппроксимации использовано следствие исходного дифференциального уравнения переноса

$ \frac{{\partial}^2 u}{\partial t^2} = c^2 \frac{{\partial}^2 u}{{\partial}x^2} $
, которое получается путем дифференцирования исходного уравнения (3.3) сначала по времени t, затем по координате x и вычитанием одно из другого получившихся соотношений.

Далее, заменяя вторую производную во втором слагаемом в правой части с точностью до O(h2), получим новую разностную схему, аппроксимирующую исходное дифференциальное уравнение с точностью 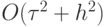O(\tau ^{2} + h^{2}). Сеточные уравнения для схемы Лакса - Вендроффа во внутренних узлах расчетных сеток есть

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + c \frac{{u_{{m} + 1}^{n} - u_{m - 1}^{n}}}{2h} - c^2 \frac{\tau}{2} \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{{m} + 1}^{n}}}{{h^2}} = 0. $

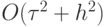Неявная шеститочечная схема возникает при q = 0 ; при \gamma = 0, 5 ее порядок аппроксимации O(\tau ^{2} + h^{2}), при \gamma = 1 - O(\tau + h^{2}).

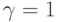Построить шаблоны схемы при \gamma = 0, 5 и при \gamma = 1.

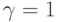Неявная нецентральная схема. Рассмотрим случай q = \sigma\ sign\ c. При \gamma = 0, 5 порядок аппроксимации — O(\tau ^{2} + h). При \gamma = 1 - O(\tau + h). Упражнение. Нарисовать шаблон схемы при \gamma = 0, 5 и при \gamma = 1.

Последние две разностные схемы носят названия схем Ландау - Меймана - Халатникова и Карлсона, соответственно.

Явная схема Бима - Уорминга

Бим и Уорминг предложили изменить метод Мак-Кормака, используя на обоих этапах односторонние разности одинаковой направленности;для линейного уравнения переноса эта схема будет

\begin{gather*} \frac{\tilde{u}_m - u_m}{\tau} + a \frac{u_m^{n} - u_{m - 1}^{n}}{h} = 0, \\ \frac{u_m^{n + 1} - \frac{1}{2}(u_m^{n} + \tilde{u}_m)}{\tau} + a \frac{\tilde{u}_m - \tilde{u}_{m - 1}}{h} + a \frac{u_m^{n} - 2u^{n}_{m - 1} + u^{n}_{m - 2}}{h^2} = 0. \end{gather*}

При подстановке первого уравнения во второе, получим

$ u_m^{n + 1} = u_m^{n} - {\sigma}(u_m^{n} - u_{m - 1}^{n}) + \frac{{\sigma}}{2}(1 - {\sigma})(u_m^{n} - 2u_{m - 1}^{n} + u_{{m} - 2}^{n}) = 0. $

Шаблоны двух - и одноэтапной схем имеют вид


Эта же схема может быть записана в приращениях

$ \Delta_{\tau} u_m^{n} = \frac{{{\sigma}({\sigma}- 1)}}{2} \Delta^{-} u_m^{n} - \frac{{{\sigma}(1 + {\sigma})}}{2} {\Delta}^{-}u_{m - 1}^{n} . $
Дальше >>
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

Вопросы и ответы

вопросов: 0