Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
Можно формально умножить правую и левую части (1.13) на i и воспользоваться приведенными выше результатами. Получим, что в случае 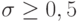 схема устойчива, а при
схема устойчива, а при 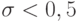 возникает условие устойчивости вида
возникает условие устойчивости вида
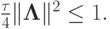
Так как
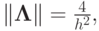
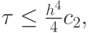
где c2 — константа, определяющая  - устойчивость схемы. При этом погрешности все равно экспоненциально возрастают! В энергетической норме
- устойчивость схемы. При этом погрешности все равно экспоненциально возрастают! В энергетической норме  условие устойчивости будет
условие устойчивости будет
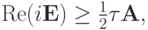
которое не выполняется при любом 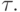 Следовательно, в энергетической норме устойчивых разностных схем для уравнения Шредингера при
Следовательно, в энергетической норме устойчивых разностных схем для уравнения Шредингера при 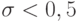 нет.
нет.
Рассмотрим разностную схему
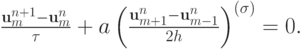
Здесь
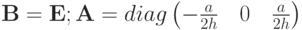
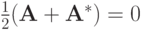
 кососимметрический.
кососимметрический.В случае 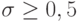 схема устойчива. При
схема устойчива. При 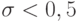 имеем условие устойчивости
имеем условие устойчивости

но ошибки все же экспоненциально возрастают как 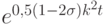 , где k — число Куранта. По спектральному признаку при
, где k — число Куранта. По спектральному признаку при 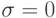 схема неустойчива.
схема неустойчива.
Очевидно, что для уравнения Шредингера нет устойчивых схем в случае 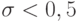 и при использовании метода конечных элементов. Действительно, будем рассматривать дискретную схему
и при использовании метода конечных элементов. Действительно, будем рассматривать дискретную схему

где  . Условие устойчивости в энергетической норме приведет к операторному неравенству вида
. Условие устойчивости в энергетической норме приведет к операторному неравенству вида
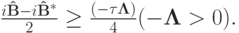
В силу положительности 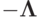 , приходим к
противоречию
, приходим к
противоречию
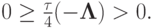
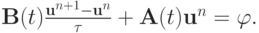
Пусть, как и ранее, выполнено условие самосопряженности
![{\mathbf{A}}(t): {\mathbf{A}}(t) = {\mathbf{A}}^* (t) > 0, t \in [0;T], \quad {\mathbf{B}}(t) > 0;](/sites/default/files/tex_cache/ee7e6d4e9b59d00f0c3c619b9a623910.png)
![|([{\mathbf{A}}(t) - {\mathbf{A}}(t -{\tau})]{\mathbf{x}}, {\mathbf{x}})| \le{\tau}c({\mathbf{A}}(t -{\tau}){\mathbf{x}}, {\mathbf{x}}).](/sites/default/files/tex_cache/0edcb7f5fda896342859f9220a23e7c9.png)
Введем энергетические нормы, зависящие от времени:
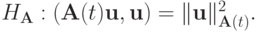
Воспользуемся введенным ранее энергетическим тождеством:
![\begin{gather*}
2{\tau}\left({\left[{{\mathbf{B}}(t) - \frac{{{\tau}{\mathbf{A}}(t)}}{2}}\right]
\frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau}, \frac{{{\mathbf{u}}^{n + 1} -
{\mathbf{u}}^{n}}}{\tau}}\right) + ({\mathbf{A}}(t){\mathbf{y}}^{n + 1},
{\mathbf{y}}^{n + 1} ) = \\
= ({\mathbf{A}}(t){\mathbf{u}}^{n + 1}, {\mathbf{u}}^{n + 1} ) + 2{\tau}\left({{\varphi},
\frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau}}\right).
\end{gather*}](/sites/default/files/tex_cache/3776a4920d2f909fd4cf9914b9c6d6f5.png)
Учтем, что
![\begin{gather*}
({\mathbf{A}}(t){\mathbf{y}}(t), {\mathbf{y}}(t)) \equiv ({\mathbf{A}}(t -{\tau})
{\mathbf{y}}(t), {\mathbf{y}}(t)) + ([{\mathbf{A}}(t) - {\mathbf{A}}(t -{\tau})]
{\mathbf{y}}(t), {\mathbf{y}}(t)) \le \\
\le (1 + \tau c)({\mathbf{A}}(t -{\tau}){\mathbf{y}}(t), {\mathbf{y}}(t))
\end{gather*}](/sites/default/files/tex_cache/8b3416158ec66bcc9d026365a4a8c8da.png)
в силу Липшиц - непрерывности. Тогда получаем
![\begin{gather*}
2{\tau}\left({\left[{{\mathbf{B}}(t) - \frac{{{\tau}{\mathbf{A}}(t)}}{2}}\right]
\frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau}, \frac{{{\mathbf{u}}^{n + 1} -
{\mathbf{u}}^{n}}}{\tau}}\right) + ({\mathbf{A}}(t){\mathbf{u}}(t +{\tau}),
{\mathbf{u}}(t +{\tau})) \le \\
\le (1 +{\tau}c) \times ({\mathbf{A}}(t -{\tau}){\mathbf{u}}^{n}, {\mathbf{u}}^{n}) + 2{\tau} \left({{\varphi}(t), \frac{{{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n}}}{\tau}}\right). \end{gather*}](/sites/default/files/tex_cache/c96351fb248a2e1c480fa43120227cb4.png)
Теперь если
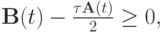
 сразу имеем
сразу имеем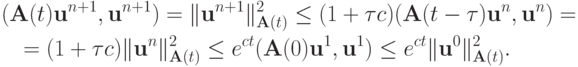
Отсюда и следует устойчивость: из энергетического тождества при n = 1 получим, что схема устойчива по начальным данным. Устойчивость по правой части будет следовать из устойчивости по начальным данным.
Таким образом, случай операторов , зависящих от времени, принципиально не отличается от случая постоянных операторов , лишь нормы устроены несколько по - другому.
Аналогичные теории строятся и для трехслойных разностных схем, условия устойчивости также получаются на основе энергетических тождеств в виде операторных неравенств.

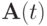 — Липшиц - непрерывен
— Липшиц - непрерывен