Лекция 1: Исследование разностных схем для эволюционных уравнений на устойчивость и сходимость
Величина погрешности решения, входящая в определение сходимости, тогда будет 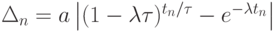 .
.
Представим  в виде
в виде
![\begin{gather*}
(1 - {\lambda}{\tau})^{t_n /{\tau}} = \exp (\frac{{t_n }}{\tau} \ln (1 - {\lambda}{\tau})) = \exp \frac{{t_n }}{\tau} \left[{- {\lambda}{\tau}+ \frac{{{\lambda}^2{\tau}^2}}{2} + O({\tau}^3 )}\right] = \\
= e^{- {\lambda}t_n } \left[{1 + \frac{{{\lambda}^2{\tau}t_n }}{2} + O({\tau}^2 )}\right] \left[{1 + O({\tau}^2 )}\right] = e^{- {\lambda}t_n } + \frac{\tau}{2} {\lambda}^2 t_n e^{- {\lambda}t_n } +
O({\tau}^2 ).
\end{gather*}](/sites/default/files/tex_cache/190d13f1e272ed8c325938fb5cfb6c9c.png)
Тогда

и, следовательно,
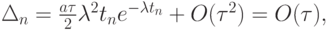
т.е. разностная схема имеет первый порядок сходимости. К сожалению, чтобы исследовать схему на сходимость, необходимо знать точное решение дифференциальной задачи. Обычно разностные схемы исследуются на аппроксимацию и устойчивость, откуда по теореме П.Лакса и В.С.Рябенького и следует сходимость, по крайней мере, для линейных задач.
Пример разностной задачи, аппроксимирующей рассматриваемое уравнение:
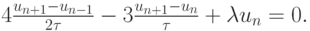
Можно показать, получив общее решение разностной задачи, что эта схема не является устойчивой и, следовательно, не имеет место сходимость решения к точному решению дифференциальной задачи.
Определение 2. Говорят, что разностная задача аппроксимирует дифференциальную на ее решении, если норма невязки, возникающей при действии разностного оператора на сеточную функцию — проекцию на сетку точного решения
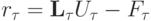
стремится к нулю при  если выполнена оценка
если выполнена оценка  ,
, 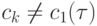 (константа, входящая в правую часть неравенства, не зависит от сеточных параметров), то имеет место аппроксимация порядка p.
(константа, входящая в правую часть неравенства, не зависит от сеточных параметров), то имеет место аппроксимация порядка p.
Приведем пример исследования разностной схемы на аппроксимацию, для чего напомним следующие соотношения, полученные с помощью разложения проекции точного решения на сетку в ряд Тейлора в окрестности одного из сеточных узлов:
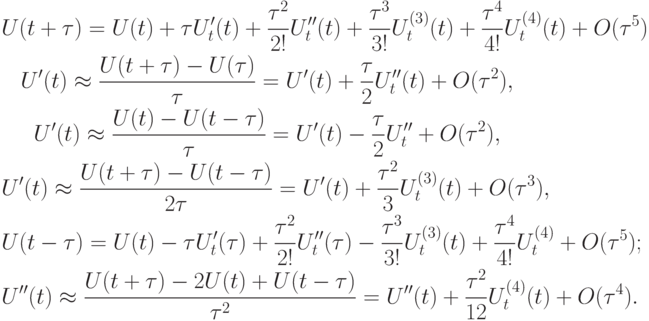
Рассмотрим задачу Коши для уравнения переноса
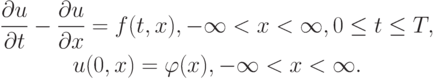
Введем разностную сетку и положим
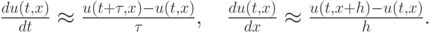
Получим введенную выше схему "правый уголок".
Положив , что функция u(t , x) имеет ограниченные вторые производные, получим выражения для главных членов погрешности аппроксимации, т.е. тех членов , которые определяются минимальными степенями сеточных параметров.
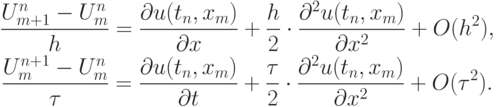
Тогда для невязки верно равенство 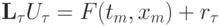 , или, так как в силу самого дифференциального уравнения
, или, так как в силу самого дифференциального уравнения
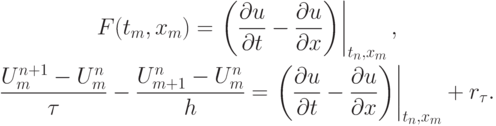
Здесь невязка 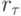 определяется выражением
определяется выражением
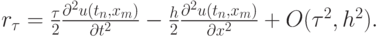
Так как  , то разностная схема имеет
первый порядок аппроксимации по
, то разностная схема имеет
первый порядок аппроксимации по 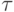 и h.
и h.
