Самостоятельная работа 7: Оптимизация и распараллеливание вычислений в задаче детектирования объектов на изображениях с использованием алгоритма Latent SVM

3. Математическая постановка задачи детектирования объектов с n частями

3.1. Построение оценочной функции положения объекта

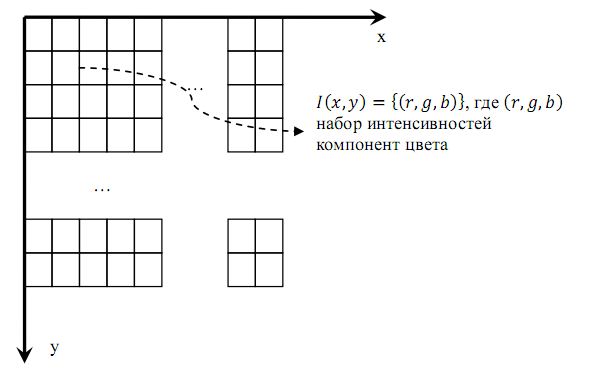
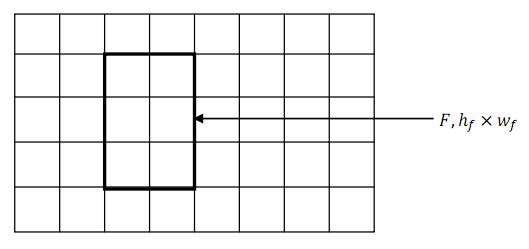
Пусть дано изображение l. Изображение представляется в виде матрицы пикселей. Каждый элемент матрицы состоит из трех компонент. Компоненты соответствуют интенсивностям цвета (RGB) в точке. Всего в изображении w элементов по горизонтали и h элементов по вертикали. В качестве входных данных для алгоритма выступает матрица, показанная на рис. 14.1.

Рис. 14.1. Матрица интенсивностей для трехканального изображения

Математической моделью изображения является карта признаков (свойств) . Фактически карта признаков представляет матрицу вещественных чисел, полученных в результате вычисления некоторой функции от интенсивностей текущего и набора окрестных пикселей.

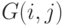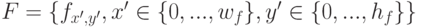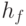Рассмотрим ситуацию, когда имеется изображение, по которому построена карта свойств , и имеется объект для поиска. Искомый объект можно описать с помощью фильтра , где и 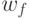– размеры фильтра изображения (рис. 14.2). Фильтр определяет набор признаков, наиболее характерных для объекта заданного класса.

Рис. 14.2. Модель объекта

Для оценки наличия объекта в конкретной области применяется следующая свертка:

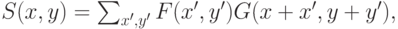( 1)

где .

Чем больше 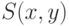, тем больше вероятность того, что искомый объект находится в точке .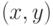

Теперь предположим, что объект состоит из n частей. Введем обозначения:

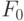• – грубый фильтр (фильтр для всего объекта),
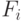• – фильтр для i-ой части объекта (точный фильтр). Заметим, что положение точного фильтра задается относительно грубого.

В этом случае оценочную функцию можно записать следующим образом:

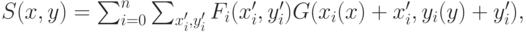( 2)

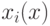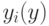где и – положение фильтра 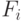в глобальных координатах изображения, а 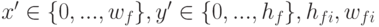– размеры точного фильтра с номером i

(2) позволяет найти на изображении объект фиксированного размера. Если объект имеет размеры, отличные от эталонного, то в этом случае, объект не будет найден. Для решения данной проблемы строят пирамиду признаков H . Пирамида признаков содержит несколько уровней, на каждом из которых находится карта свойств изображения, полученного в результате уменьшения или увеличения исходной картинки. На уровне находится карта свойств исходного изображения, а на 0-ом уровне – карта свойств изображения, которое увеличено в два раза.

Далее предполагается, что фильтр может быть расположен на любом уровне пирамиды признаков. Как следствие, чтобы определить положение фильтра в исходном изображении и его масштаб, необходимо знать номер уровня и положение левого верхнего угла фильтра на уровне. Пусть 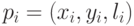– положение фильтра 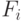на уровне 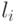в пирамиде признаков H.

Введем функцию 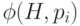, которая получается из пирамиды признаков H и координат положения 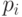конкретное свойство изображения, путем вычисления глобальных координат x и y фильтра 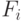на слое l. Тогда оценочную функцию можно записать следующим образом:

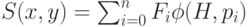( 3)

До настоящего момента в построенной модели все части изображения были никак не связаны и могли располагаться в любой части входной картинки. Для реального объекта это не так (например, руки человека не могут быть удалены бесконечно далеко от туловища). Пусть заданы модели частей объекта 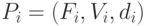, где 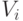– идеальное расположение его части, а 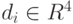– коэффициенты квадратичной функции штрафа 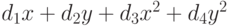, которая вносит вклад в значение оценочной функции в случае чрезмерного удаления части от самого объекта. Тогда модель для объекта с n частями формально определяется множеством параметров (4).

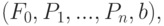( 4)

где параметр определяет соответствие коэффициентов между моделями. Таким образом, оценочная функция имеет вид (5).

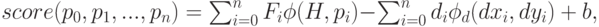( 5)

где первое слагаемое – результат применения фильтров к исходному изображению (значения сверток грубого и точных фильтров с конкретной матрицей признаков), второе слагаемое – штраф за счет деформации взаимного расположения частей, b – параметр соответствия коэффициентов между моделями, а 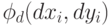– вектор с компонентами 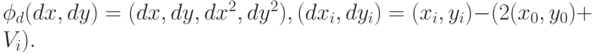. В результате оценочную функцию можно записать в свернутом виде (6), если ввести дополнительные обозначения.

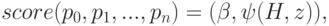( 6)

где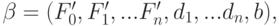

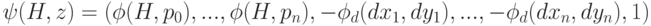
3.2. Поиск частично видимых объектов

Предположим, что имеется модель 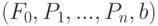для объекта с частями Построена пирамида признаков для исходного изображения. Для определения положения частично видимых объектов при вычислении сверток каждую матрицу признаков в пирамиде необходимо дополнить нулевыми границами. Размер границы определяется максимальными размерами фильтров по каждому измерению согласно формулам (7).

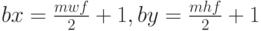( 7)

где .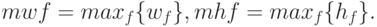

При вычислении сверток с грубым фильтром матрица признаков дополняется нулевой границей, размер которой определяется в соответствии с приведенными формулами, с точными фильтрами данная граница должна быть удвоена.