|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Самостоятельная работа 7: Оптимизация и распараллеливание вычислений в задаче детектирования объектов на изображениях с использованием алгоритма Latent SVM
12.2. Приложение Б. Применение двумерного быстрого преобразования Фурье для вычисления сверток
12.2.1. Постановка задачи
Входные данные:
- Двумерная матрица векторов признаков
 (матрица
признаков на некотором уровне пирамиды признаков). Данная матрица
может быть представлена в виде трехмерного прямоугольного
параллелепипеда размерности
(матрица
признаков на некотором уровне пирамиды признаков). Данная матрица
может быть представлена в виде трехмерного прямоугольного
параллелепипеда размерности 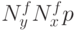 , где
, где 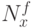 – число столбцов
матрицы векторов,
– число столбцов
матрицы векторов, 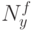 - количество строк матрицы векторов,
- количество строк матрицы векторов, 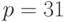 –
размерность вектора признаков. Двумерную матрицу, полученную при
каждом фиксированном p , будем называть каналом.
–
размерность вектора признаков. Двумерную матрицу, полученную при
каждом фиксированном p , будем называть каналом. - Двумерная матрица весовых векторов фильтра
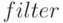 (это может быть
точный или грубый фильтр). Данная матрица может быть представлена
в виде трехмерного прямоугольного параллелепипеда размерности
(это может быть
точный или грубый фильтр). Данная матрица может быть представлена
в виде трехмерного прямоугольного параллелепипеда размерности 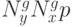 , где
, где
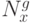 – число столбцов матрицы весовых векторов,
– число столбцов матрицы весовых векторов, 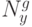 –
количество строк матрицы весовых векторов,
–
количество строк матрицы весовых векторов, 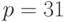 – размерность
вектора весов.
– размерность
вектора весов.
Выходные данные: двумерная матрица свертки 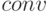 размерности
размерности
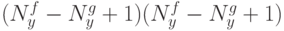
Задача: определить значения элементов матрицы свертки в соответствии с формулой
![conv[i,j]=\sum^{N^g_y-1}_{di=0} \sum^{N^g_x-1}_{dj=0} \sum^{p-1}_{k=0} filter[di,dj,k]*featureMap[i+di,j+dj,k]](/sites/default/files/tex_cache/cd1bca95c71c86f9050e5b327d1b80d9.png)
12.2.2. Этапы решения
-
Для каждого канала
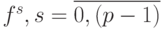 матрицы векторов признаков
матрицы векторов признаков
 оперделяем образ Фурье. Для этого используется
двумерное дискретное преобразование Фурье. Для вычисления
двумерного преобразования применяется одномерное БПФ сначала к
строкам, потом к столбцам (или наоборот):
оперделяем образ Фурье. Для этого используется
двумерное дискретное преобразование Фурье. Для вычисления
двумерного преобразования применяется одномерное БПФ сначала к
строкам, потом к столбцам (или наоборот): 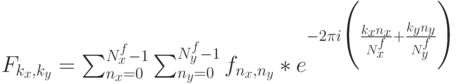
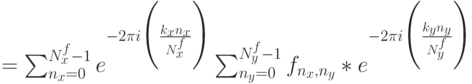
где
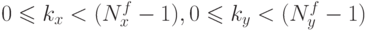 .
.При вычислении значений оценочной функции на фиксированном уровне операцию достаточно сделать один раз для всех точных фильтров и один раз для грубого фильтра, т.к. свертки с грубыми и точными фильтрами считаются на разных уровнях пирамиды признаков.
-
Для каждого канала
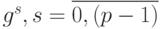 матрицы весовых векторов
фильтра
матрицы весовых векторов
фильтра  получаем образ Фурье. Для этого матрицу весов
каждого канала необходимо повернуть на
получаем образ Фурье. Для этого матрицу весов
каждого канала необходимо повернуть на  и дополнить нулями до
размерности матрицы признаков, затем применить двумерное
дискретное преобразование Фурье (аналогично применяется
одномерное преобразование последовательно к строкам и столбцам):
и дополнить нулями до
размерности матрицы признаков, затем применить двумерное
дискретное преобразование Фурье (аналогично применяется
одномерное преобразование последовательно к строкам и столбцам): 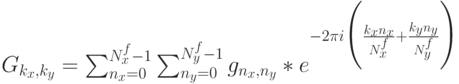
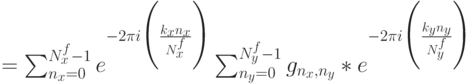
где
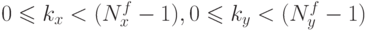
- Для каждого канала находим свертку образов Фурье
 :
:
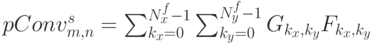
где
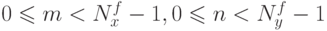
- Находим суммарную свертку по всем каналам
 :
:
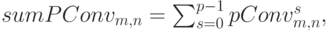 где
где 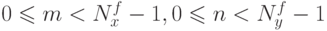
- Определяем прообраз Фурье для свертки, используя одномерное
преобразование Фурье:
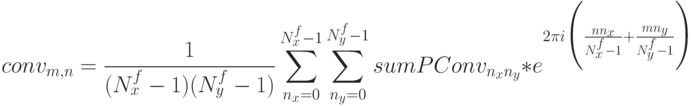
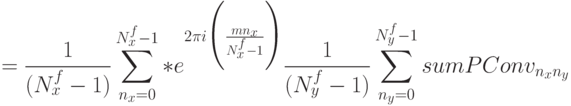 где
где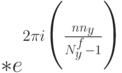
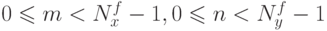
12.2.3. Одномерное дискретное преобразование Фурье
Постановка задачи:
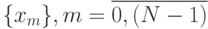 – последовательность действительных чисел, N -
произвольное число (в общем случае составное).
– последовательность действительных чисел, N -
произвольное число (в общем случае составное).
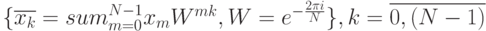 – множество образов Фурье
для последовательности
– множество образов Фурье
для последовательности  .
.
Задача состоит в том, чтобы определить множество образов Фурье.
Алгоритм:
Пусть  имеет два простых множителя
имеет два простых множителя 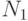 и
и 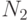 . Тогда любые
. Тогда любые  и
и  можно
представить в виде
можно
представить в виде 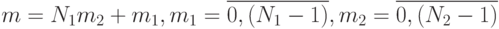 и
и
 . Как следствие, каждый
элемент последовательности образов Фурье выражается следующим
образом:
. Как следствие, каждый
элемент последовательности образов Фурье выражается следующим
образом:
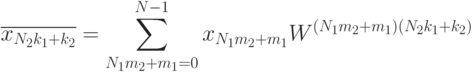
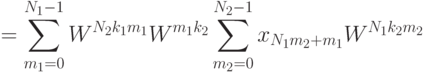
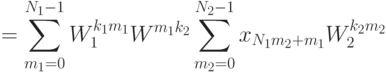
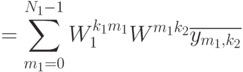
где
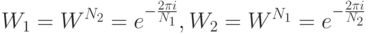
В случае, когда N – произвольное составное число, которое имеет больше простых множителей, чем два, указанная процедура выполняется рекурсивно. Сначала N представляется в виде произведения пары составных множителей. Затем для каждого выполняется разложение на два сомножителя. Эта процедура выполняется до тех пор, пока следующие множители не окажутся простыми числами.


 "
"