Самостоятельная работа 7: Оптимизация и распараллеливание вычислений в задаче детектирования объектов на изображениях с использованием алгоритма Latent SVM

3.3. Приведение задачи вычисления значений оценочной функции к задаче оптимизации

Для того чтобы определить значение оценочной функции для некоторого положения объекта в рамках координат матрицы признаков, необходимо решить задачу вида (8).

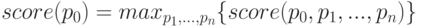( 8)

Данная задача предполагает выбор положений частей, при которых достигается максимальное значение оценочной функции для заданного положения грубого фильтра.

Подставим максимизируемую функцию в данное выражение и выполним некоторые элементарные преобразования:

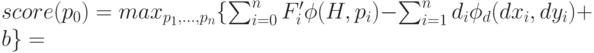
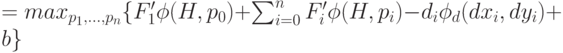( 9)

Поскольку первое и последнее слагаемое в функции под максимумом не зависят от аргументов, по которым проводится максимизация, то их можно вынести из-под максимума:

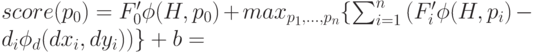
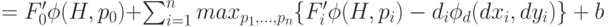( 10)

Далее введем вспомогательные обозначения:

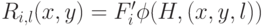
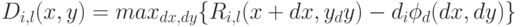
Как следствие, оценка положения объекта вычисляется следующим образом:

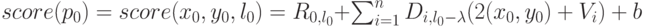
Из формулы видно, что для вычисления оценки необходимо решить несколько задач оптимизации вида:

Такого рода задачи приводятся к задаче вычисления обобщенного преобразования расстояний (случай евклидова расстояния на двумерной сетке):

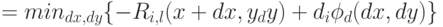
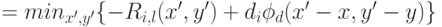
где .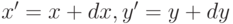

Очевидно, что при 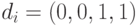функция 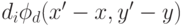представляет собой Евклидово расстояние, т.к. :

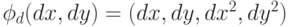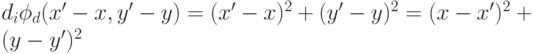
Как следствие, получаем задачу минимизации выпуклой функции, которая решается с использованием обобщенного метода преобразования расстояний (Приложение А. Обобщенный метод преобразования расстояний для решения задачи оптимизации, [15]).

Задача выбора наиболее вероятных положений объекта предполагает выбор тех положений грубого фильтра, для которых выполняется условие (11).

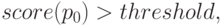( 11)

где threshold – некоторое пороговое значение оценочной функции, которое является параметром модели. Поиск положений, удовлетворяющих указанному условию, осуществляется в результате прохода по всем уровня пирамиды. В результате останется только пересчитать координаты прямоугольников, полученных на каждом уровне, в координаты исходного изображения.

4. Основные этапы решения задачи детектирования с использованием алгоритма Latent SVM

Начальным этапом алгоритма Latent SVM является построение пирамиды признаков – модели исходного изображения^{1Процедура построения пирамиды признаков в настоящей работе не описывается, т.к. время выполнения данного этапа вносит незначительный вклад в общее время поиска объектов на наборе тестовых данных VOC 2007.}. Процедура включает следующие действия:

1. Масштабирование исходного изображения. Результатом является пирамида изображений.
2. Построение матриц векторов признаков для каждого изображения в пирамиде изображений – формирование пирамиды признаков.

Построенная математическая модель изображения используется для определения расположения прямоугольника, окаймляющего объект. Для решения задачи детектирования необходима модель, описывающая класс объектов. Математическая модель типичного представителя объекта была описана в предыдущем разделе (грубый фильтр и набор точных фильтров).

Идея алгоритма определения положения объекта состоит в том, чтобы некоторым образом оценить вероятность нахождения объекта во всех возможных положениях пирамиды изображений и выбрать наиболее вероятные положения. Данный алгоритм включает следующие этапы:

1. Вычисление значений оценочной функции для каждого возможного положения объекта, исходя из формул для вычисления 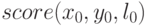. Положение объекта определяется расположением левого верхнего угла грубого фильтра в матрице векторов признаков какого-либо уровня. Заметим, что оценочная функция строится как сумма скалярных произведений векторов (свертка) признаков грубого и точных фильтров модели с соответствующими векторами матрицы признаков. На каждом уровне пирамиды вычисления проводятся независимо.
2. Выбор положений, для которых значения оценочной функции превышают пороговое значение (11). Полученные координаты определяют положение грубого фильтра, описывающего объект, в матрице признаков.
3. Преобразование координат, соответствующих найденным положениям объекта на различных уровнях пирамиды признаков, в пиксельные координаты исходного изображения. Полученное множество точек – координаты левых верхних углов окаймляющих прямоугольников.

Более подробное описание метода Latent SVM приведено в работе [3].