|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 4: Отслеживание движения и алгоритмы сопровождения ключевых точек
1.3. Полный перебор допустимых вариантов смещения изображений или их фрагментов. Возможные способы ускорения перебора
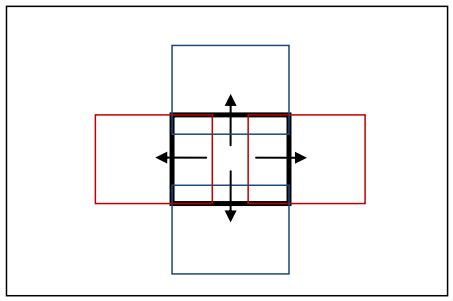
Еще один простейший способ оценить движение на нескольких изображениях – перебрать все возможные варианты смещений изображений или их отдельных фрагментов (translational alignment, [5, гл. 8.1]). Для этого первоначально необходимо выбрать метрику для оценки степени сходства фрагментов. Как следствие, исходная задача определения движения может быть сведена к минимизации функции ошибки по всем возможным направлениям смещения (рис.4.2).
В предположении, что имеется последовательность полутоновых изображений, приведем наиболее распространенные функции ошибки.
- 1. Квадратичная функция ошибки (4.19).
где
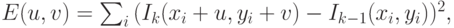
( 4.19) 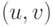 – вектор смещения изображения или фрагмента.
– вектор смещения изображения или фрагмента.
- 2. Грубые оценочные функции ошибки. Общий вид функций данной
группы определяется формулой (4.20). При этом
 – функция, которая
имеет меньшую степень роста по сравнению квадратичной функцией.
Примером грубой функции ошибки может служить сумма абсолютных разностей (4.21).
– функция, которая
имеет меньшую степень роста по сравнению квадратичной функцией.
Примером грубой функции ошибки может служить сумма абсолютных разностей (4.21).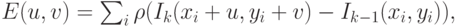
( 4.20) 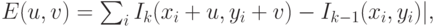
( 4.21) - 3. Взвешенная квадратичная функция ошибки (4.22). Весовые
коэффициенты – дискретные функции, которые принимают нулевые
значения за пределами изображения.
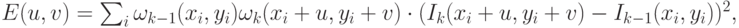
( 4.22) - 4. Кросс-корреляция пары выровненных изображений (4.23).
Заметим, что при выборе кросс-корреляции в качестве функции ошибки выполняется не минимизация, а максимизация по всем
возможным направлениям смещения.
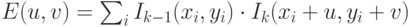
( 4.23)
В общем случае если задан набор цветных изображений, то всегда можно выполнить их конвертирование в полутоновые, либо ввести дополнительную сумму по числу каналов, и использовать одну из предложенных функций ошибки.
На практике полный перебор работает достаточно медленно, поэтому часто применяется иерархическая схема. Конструируется пара пирамид для последовательно идущих изображений посредством масштабирования исходных изображений. Последующий поиск выполняется от мелких изображений к более крупным, в результате чего постепенно отсекаются направления смещения, в которых заведомо не происходит движение. Если на некотором уровне обнаружился вектор смещения для определенного фрагмента, то на следующем – этот вектор используется для предсказания расположения соответствующего фрагмента. Иерархическая схема не всегда позволяет получить качественный результат, т.к. часто невозможно увеличить/уменьшить изображение до определенных размеров и при этом не размыть необходимые признаки для поиска областей движения.
Еще один способ ускорения вычисления при реализации переборной схемы – использование подхода, основанного на вычислении быстрого преобразования Фурье (БПФ) [30]. Метод опирается на тот факт, что модули образов Фурье исходного и смещенного сигналов связаны уравнением (4.24).
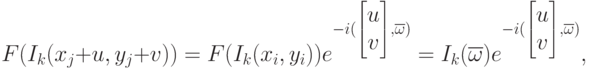 |
( 4.24) |
где 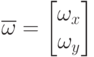 – вектор частот двумерного БПФ,
– вектор частот двумерного БПФ, 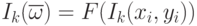 –
образ Фурье сигнала
–
образ Фурье сигнала 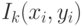 . Допустим, что в качестве функции ошибки
выбрана кросс-корреляция, вычислим БПФ от этой функции (4.25). В
результате получаем преобразование Фурье от свертки функций. Исходя из
свойств преобразования, образ Фурье от полученной свертки функций –
произведение образа
. Допустим, что в качестве функции ошибки
выбрана кросс-корреляция, вычислим БПФ от этой функции (4.25). В
результате получаем преобразование Фурье от свертки функций. Исходя из
свойств преобразования, образ Фурье от полученной свертки функций –
произведение образа 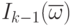 первой функции на комплексно-
сопряженный образ
первой функции на комплексно-
сопряженный образ 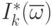 второй функции.
второй функции.
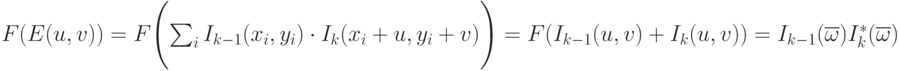 |
( 4.25) |
Отсюда эффективность оценивания кросс-корреляции с использованием
преобразования Фурье очевидна. Достаточно вычислить образы Фурье для
исходной пары изображений с помощью БПФ (сложность составляет
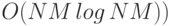 для изображения размера
для изображения размера  , перемножить
полученные образы (за время, не превышающее
, перемножить
полученные образы (за время, не превышающее  ) , затем
вычислить обратное преобразование Фурье. В результате получится
матрица значений кросс-корреляционной функции, из которой необходимо
выбрать максимальное значение. Приведенный пример не является
единственным примером ускорения вычислений функции ошибки с
помощью БПФ [5].
) , затем
вычислить обратное преобразование Фурье. В результате получится
матрица значений кросс-корреляционной функции, из которой необходимо
выбрать максимальное значение. Приведенный пример не является
единственным примером ускорения вычислений функции ошибки с
помощью БПФ [5].
Для некоторых практических приложений, в частности, для стабилизации видео необходима субпиксельная точность определения смещения – смещение в дробных координатах. Один из наиболее известных подходов состоит в том, чтобы использовать процедуру уточнения направления смещения. Впервые была введена при разработке алгоритма сопровождения Лукаса-Канаде, о котором речь пойдет в одном из следующих разделов. Процедура основана на применении метода градиентного спуска для минимизации квадратичной функции ошибки в смещенной точке – функции энергии (4.26), которая приближается разложением в ряд Тейлора.
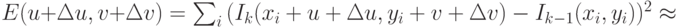 |
( 4.26) |
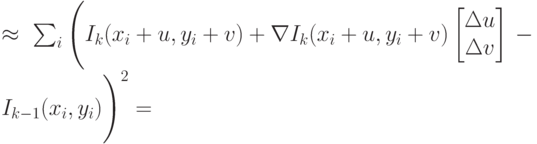
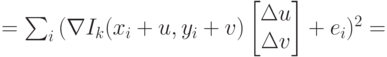
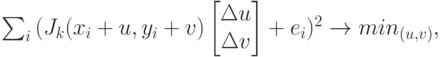 |
( 4.27) |

![J_k(x_i+u,y_i+v)=\nabla I_k(x_i+u,y_i+v)=[\frac {\deltaI_k} {\delta x},\frac {\deltaI_k} {\delta y}]\rvert_{(x_i+u,y_i+v)}](/sites/default/files/tex_cache/504ba8d32dbfd485d871b36efa652a88.png)
Полученная задача минимизации (4.27) сводится к решению системы линейных алгебраических уравнений вида (4.28). Доказательство данного факта можно найти в [31].
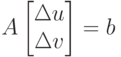 |
( 4.28) |
где 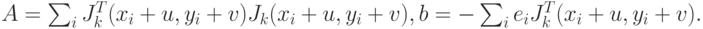 .
.
Эффективность решения задачи достигается за счет того, что для текущего
изображения градиенты 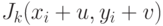 в смещенной точке можно
приближенно заменить градиентами предыдущего изображения
в смещенной точке можно
приближенно заменить градиентами предыдущего изображения  в исходной точке, т.е.
в исходной точке, т.е. 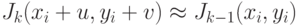 .
.
Несмотря на вычислительную сложность полного перебора, такой подход к определению движения имеет место, и вполне применим в задачах, не требующих решения в реальном времени.

 "
"