|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 4: Отслеживание движения и алгоритмы сопровождения ключевых точек
2.4. Методы сопровождения объектов, основанные на вычислении оптического потока
С каждым пикселем изображения можно связать некоторый вектор скорости, который определяет, какое расстояние "прошел" пиксель в течение временного промежутка между предыдущим и текущим кадрами. Такая конструкция, построенная для каждого пикселя изображения, представляет собой плотный оптический поток. Одним из наиболее известных алгоритмов сопровождения, основанных на вычислении плотного оптического потока, является метод Хорна (Horn-Schunk method) [8, 25]. По существу данный метод предполагает решение системы дифференциальных уравнений, полученных в задаче математического программирования (раздел 1.6), с помощью итерационных методов для построения компонент вектора скорости в каждой точке изображения.
Другой класс алгоритмов, использующих плотный оптический поток, – алгоритмы сопоставления блоков (block matching algorithms, [8]). Идея состоит в том, что предыдущее и текущее изображения разбиваются на блоки, как правило, квадратные и перекрывающиеся, а затем определяется движение этих блоков посредством сопоставления. Поскольку алгоритмы сопоставления работают с блоками, то изображение поля скоростей обычно имеет меньшее разрешение по сравнению с исходным изображением.
Алгоритм Лукаса-Канаде (Lucas-Kanade) основан на вычислении разреженного оптического потока, т.е. на построении векторного поля скоростей для выделенного набора точек. Задача слежения без учета аффинных искажений с помощью данного алгоритма сводится к поиску оптического потока в особых точках [26]. Впоследствии появились модификации данного алгоритма Томаши-Канаде (Tomasi-Kanade) и Ши- Томаши-Канаде (Shi-Tomasi-Kanade). Трекер Ши-Томаши-Канаде впервые учитывает аффинные искажения окрестных точек. Также существует модификация метода для случая переменного освещения [27].
В литературе можно обнаружить различные модификации перечисленных методов. В [28] предлагается сравнение производительности различных алгоритмов сопровождения с использованием оптического потока.
2.5. Применение метода "сдвиг среднего" к решению задачи сопровождения
Несколько в стороне стоят методы сопровождения, основанные на использовании техники "сдвиг среднего" (mean shift) [8, 23, 24]. Идея методов состоит в том, что для каждой особой точки (в общем случае, для каждого объекта) выбирается окно поиска, вычисляется центр масс распределения интенсивностей (гистограммы). Соответственно центр окна смещается в центр масс, который представляет собой положение точки на текущем кадре. Определение положения точки на последующих кадрах сводится к применению очередного шага метода "сдвига среднего". Метод останавливается, когда центр масс перестает смещаться.
2.6. Применение фильтра Кальмана для оценки положения объекта
Задачу сопровождения можно рассматривать как хорошо изученную проблему теории управления, которая состоит в том, чтобы оценить состояние системы на основании последовательности зашумленных измерений [9]. Формально имеется модель объекта, которая наблюдается в зашумленном пространстве сцены. Обозначим через x – модель объекта, z – наблюдение объекта. В общем случае x,z – вектора признаков, которые вполне могут иметь разную размерность. В процессе сопровождения объекта модели и наблюдения могут использоваться двумя способами:
- Последовательность наблюдений
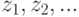 применяется для уточнения
базовой модели x . Заметим, что модель с течением времени также
может изменяться, поэтому каждое новое наблюдение
применяется для уточнения
базовой модели x . Заметим, что модель с течением времени также
может изменяться, поэтому каждое новое наблюдение 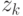 может давать
новую оценку модели
может давать
новую оценку модели 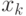 .
. - Построенная оценка модели
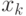 используется для предсказания модели
используется для предсказания модели
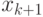 и наблюдения
и наблюдения 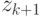 .
.
В результате получаем механизм обратной связи: наблюдаем 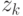 , оцениваем
, оцениваем
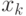 , предсказываем
, предсказываем 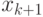 и
и 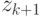 , обновляем
, обновляем 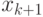 на основании
на основании 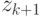 . Такой
механизм лежит в основе методов сопровождения, основанных на
фильтрах Кальмана и фильтрах частиц. В данном разделе остановимся на
применении фильтра Кальмана.
. Такой
механизм лежит в основе методов сопровождения, основанных на
фильтрах Кальмана и фильтрах частиц. В данном разделе остановимся на
применении фильтра Кальмана.
Фильтр работает в предположении, что система является линейной (наблюдение являются линейной функции состояния) и шумы описываются Гауссовым распределением с математическим ожиданием, равным нулю. Тогда модель обратной связи может быть описана векторными уравнениями (4.40) и (4.41).
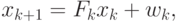 |
( 4.40) |
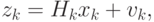 |
( 4.41) |
где 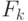 – матрица преобразования состояния системы;
– матрица преобразования состояния системы; 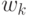 – "белый" шум с
нормальным распределением
– "белый" шум с
нормальным распределением 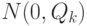 с математическим ожиданием,
равным 0, и матрицей ковариации
с математическим ожиданием,
равным 0, и матрицей ковариации 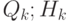 – матрица связи модели и
наблюдения;
– матрица связи модели и
наблюдения;  – "белый" шум с нормальным распределением
– "белый" шум с нормальным распределением 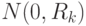 .
Заметим, что по определению матрицы ковариации
.
Заметим, что по определению матрицы ковариации 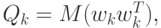 ,
,
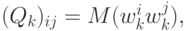 .5Если X,Y – две случайные величины, определенные на одном и том же вероятностном
пространстве, тогда ковариация численно равна математическому ожиданию от
произведения случайных величин X-MX и Y-MY , где MX,MY – математическое
ожидание случайных величин X,Y , т.о. cov(x,Y)=M((x-MX)(Y-MY)).
.5Если X,Y – две случайные величины, определенные на одном и том же вероятностном
пространстве, тогда ковариация численно равна математическому ожиданию от
произведения случайных величин X-MX и Y-MY , где MX,MY – математическое
ожидание случайных величин X,Y , т.о. cov(x,Y)=M((x-MX)(Y-MY)).
Приведем пример модели для случая равномерного движения [8]. Состояние системы определяется положением и скоростью точки, тогда состояние может быть представлено вектором вида (4.42).
 |
( 4.42) |
Матрица преобразования состояния 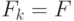 и, исходя из физических
соображений, может быть записана согласно (4.43).
и, исходя из физических
соображений, может быть записана согласно (4.43).
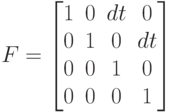 |
( 4.43) |
Поскольку при сопровождении камера регистрирует только координаты
положения объекта, то 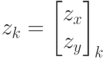 Поэтому матрицу связи наблюдения и
предсказания
Поэтому матрицу связи наблюдения и
предсказания  можно записать в соответствии с (4.44).
можно записать в соответствии с (4.44).
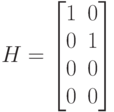 |
( 4.44) |
Т.к. в реальных условиях нельзя наблюдать равномерное движение, то
вводится Гауссов шум с матрицей ковариации
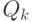 . Матрица ковариации
. Матрица ковариации
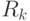 строится, исходя из того, насколько точно выполняются измерения
положения объекта.
строится, исходя из того, насколько точно выполняются измерения
положения объекта.
Теперь необходимо получить обобщенные уравнения для обновления
состояния и модели. Идея состоит в том, что сначала строится априорная
оценка 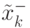 состояния согласно (4.40):
состояния согласно (4.40):
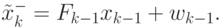 |
( 4.45) |
Затем с использованием построенной оценки вычисляется наблюдение
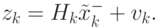 |
( 4.46) |
Также можно определить апостериорную оценку 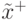 состояния, которая
строится после наблюдения. Введем ошибки
состояния, которая
строится после наблюдения. Введем ошибки
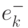 (4.47) и
(4.47) и
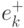 (4.48), связанные с
каждой оценкой состояния.
(4.48), связанные с
каждой оценкой состояния.
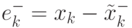 |
( 4.47) |
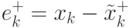 |
( 4.48) |
Фильтр Кальмана оперирует разностью 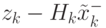 , в которую вносит вклад
ошибка
, в которую вносит вклад
ошибка 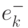 и случайный шум
и случайный шум  . В идеальном случае шум отсутствует и
оценка состояния идеальна, поэтому указанная разность обращается в
ноль. Задача состоит в том, чтобы построить матричный
коэффициент Кальмана
. В идеальном случае шум отсутствует и
оценка состояния идеальна, поэтому указанная разность обращается в
ноль. Задача состоит в том, чтобы построить матричный
коэффициент Кальмана 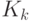 с целью обновления апостериорной оценки
согласно (4.49). Отсюда, если
с целью обновления апостериорной оценки
согласно (4.49). Отсюда, если 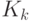 известен, то известен закон получения
обновленной модели
известен, то известен закон получения
обновленной модели 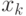 .
.
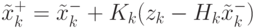 |
( 4.49) |
Уравнения (4.47) – (4.49) позволяют получить выражение связи априорной и апостериорной ошибки (4.50).
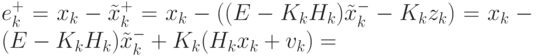 |
( 4.50) |
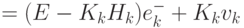
Из определения матрицы ковариации пары случайных величин следуют выражения (4.51).
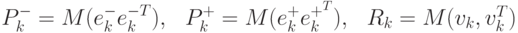 |
( 4.51) |
Вследствие независимости ошибок
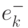 и
и 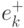 получаем нулевую ковариацию
для величин
получаем нулевую ковариацию
для величин
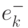 и
и  (4.52).
(4.52).
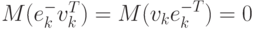 |
( 4.52) |
Проделав несложные преобразования (4.53) (умножение (4.50) на
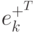 и
определение математического ожидания от полученного выражения),
можно перейти к уравнению с матрицами ковариации (4.54).
и
определение математического ожидания от полученного выражения),
можно перейти к уравнению с матрицами ковариации (4.54).

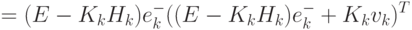

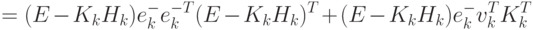
 |
( 4.53) |
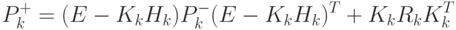 |
( 4.54) |
Отсюда получаем, что матрицу 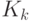 необходимо выбрать так, чтобы сумма
диагональных элементов (след) матрицы
необходимо выбрать так, чтобы сумма
диагональных элементов (след) матрицы 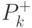 был минимален.
был минимален.
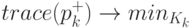 |
( 4.55) |
Решение данной задачи определяется посредством дифференцирования
функции  по
по 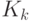 (4.56)6Результат дифференцирования получается благодаря применению свойства
(4.56)6Результат дифференцирования получается благодаря применению свойства
 при условии, что матрица B является симметричной..
при условии, что матрица B является симметричной..
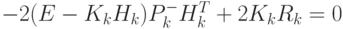 |
( 4.56) |
Как следствие, получаем формулу (4.57) для вычисления матрицы 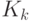 .
.
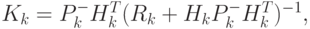 |
( 4.57) |
где
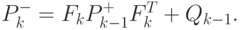 |
( 4.58) |
Заметим, что посредством несложных математических выкладок можно вывести формулу (4.59) для вычисления
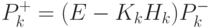 |
( 4.59) |
Подводя итог, более четко выделим схему работы фильтра:
- Предсказание. Предполагает вычисление априорной оценки
состояния
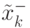 (4.45) и наблюдения
(4.45) и наблюдения 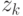 (4.46).
(4.46).
- Коррекция. Включает определение матричного коэффициента
Кальмана
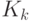 (4.57) и построение апостериорной оценки состояния
(4.57) и построение апостериорной оценки состояния  согласно (4.49).
согласно (4.49).

 "
"