Лекция 11: Метод наискорейшего спуска. Метод Давидона – Флетчера – Пауэлла. Проблема оврагов. Проблема многоэкстремальности
3. Проблема оврагов
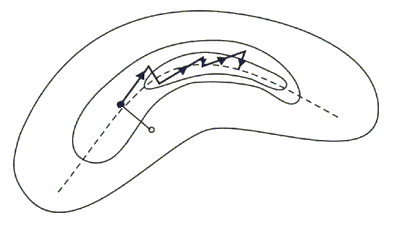
Выше нами были рассмотрены 3 варианта методов спуска, такие, как метод покоординатного спуска, метод градиентного спуска и метод наискорейшего спуска, и при этом наглядно показали, как хорошо они работают. В результате у вас могло сложиться впечатление, что проблема решена. На самом деле это не так. Все было хорошо потому, что был выбран "удобный" пример. Но посмотрите на рис. 11.4. На нем также показаны линии уровня некоторой функции. Линии уровня сильно вытянуты в одном направлении и сплющены в другом. Они напоминают рельеф местности с оврагом. Этот случай крайне неудобен для описанных выше методов.
Действительно, попытаемся найти наименьшее значение такой функции с помощью градиентного спуска. Двигаясь все время в направлении антиградиента, мы быстро спустимся на дно "оврага" и, поскольку движение идет хотя и маленькими, но конечными шагами, проскочим его. Оказавшись на противоположной стороне "оврага" и вычислив там градиент функции, мы будем вынуждены развернуться почти на 180° и сделать один или несколько шагов в обратном направлении. При этом мы снова проскочим дно "оврага" и вернемся на его первоначальную сторону. Продолжая этот процесс, мы вместо того, чтобы двигаться по дну "оврага" в сторону его понижения, будем совершать зигзагообразные скачки поперек "оврага", почти не приближаясь к цели. Таким образом, в случае "оврага" (этот нематематический термин прочно закрепился в литературе) описанные выше методы спуска оказываются неэффективными.
Для борьбы с "оврагами" был предложен ряд специальных приемов. Один из них заключается в следующем. Из двух близких точек совершают градиентный спуск на дно "оврага". Потом соединяют найденные точки прямой и делают вдоль нее большой (овражный) шаг. Из найденной точки снова спускаются на дно "оврага" и делают второй овражный шаг. В результате, двигаясь достаточно быстро вдоль "оврага", приближаемся к искомому наименьшему значению целевой функции (см. рис. 11.4). Такой метод достаточно эффективен для функций двух переменных, однако при большем числе переменных могут возникнуть трудности.
Все описанные выше методы приспособлены к случаю, когда наименьшее значение функции достигается внутри рассматриваемой области, и становятся малоэффективными, если наименьшее значение достигается на границе или вблизи нее. Для решения таких задач приходится разрабатывать специальные методы. Мы не будем на них останавливаться. Вам должно быть и без того ясно, что большое число специальных методов - это признак слабости, а не силы. Ведь приступая к решению практической задачи, мы, как правило, не знаем всех ее особенностей и не можем сразу выбрать наиболее эффективный метод.
4. Проблема многоэкстремальности
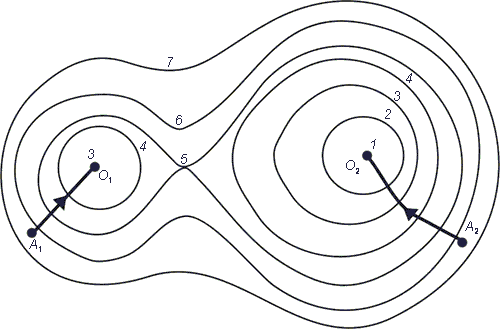
На рис. 11.5 приведены линии уровня функции с двумя локальными минимумами в точках O1 и O2. Такие функции принято называть многоэкстремальными. Сравнивая между собой значения функции в точках O1 и O2 f1=3, f2=1, находим, что наименьшее значение функция достигает в точке O2.
Представьте себе теперь, что, не имея перед глазами рис. 11.5 и не зная о многоэкстремальности функции, мы начали поиск наименьшего значения с помощью метода градиентного спуска из точки A1. Поиск приведет нас в точку O1, которую ошибочно можно принять за искомый ответ. С другой стороны, если мы начнем поиск с точки A2, то окажемся на правильном пути и быстро придем в точку O2.
Как бороться с многоэкстремальностью? Универсального ответа на этот вопрос нет. Самый простой прием состоит в том, что проводят поиск несколько раз, начиная его с разных точек. Если при этом получаются разные ответы, то сравнивают в них значения целевой функции и выбирают наименьшее. Расчеты останавливают после того, как несколько новых поисков не меняют полученного ранее результата. Выбор начальных точек поиска, обоснованность прекращения расчетов в значительной степени зависят от опыта и интуиции специалистов, решающих задачу.