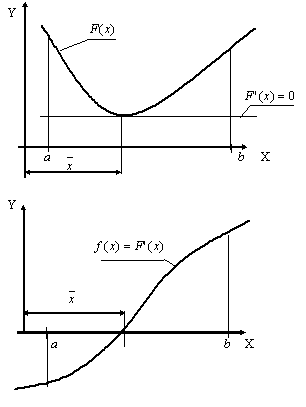Лекция 9: Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.
3. Метод Ньютона
Следующий из рассматриваемых методов однопараметрической оптимизации является градиентным методом второго порядка. В нем при поиске экстремума целевой функции используется ее первые и вторые производные. Этот метод носит название метода Ньютона.
Метод применим для вогнутой (или выпуклой), функции F(x), что соответствует монотонности ее первой производной f(x).
Известно, что если функция F(x) имеет локальный
минимум (или максимум) в точке  , то в
этой точке градиент функции F(x) (вектор ее
производных) равен нулю, т.е.
, то в
этой точке градиент функции F(x) (вектор ее
производных) равен нулю, т.е.
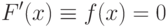
Следовательно, если функция F(x) дифференцируема, то для нахождения ее экстремума нужно решить уравнение
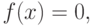 |
( 3.1) |
 .
.  - корень уравнения (3.1), точка, то
есть, координата в которой F'(x)=0, а функция F(x) имеет минимум (или максимум)
(рис.9.8).
- корень уравнения (3.1), точка, то
есть, координата в которой F'(x)=0, а функция F(x) имеет минимум (или максимум)
(рис.9.8).Алгоритм метода Ньютона сводится к линейному представлению функции f(x) и решению уравнения (3.1).
Разложим функцию f(x) в ряд Тейлора:
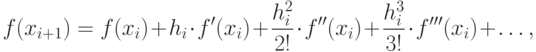
Отбросим члены ряда, содержащие 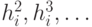 .
.
В результате имеем:

Тогда
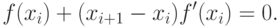
Отсюда точка экстремума равна:
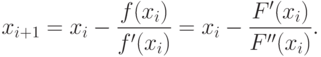 |
( 3.2) |
Для нахождения экстремума функции F(x) необходимо на каждом шаге итерационного процесса поиска определить первую F1 и вторую F2 производные целевой функции F(x), т.е.
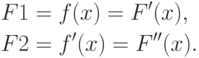
Начальные приближения х рекомендуется выбирать в той точке интервала [a,b], где знаки функции f(x) и ее кривизны f''(x) совпадают, т.е. выполняется условие
 |
( 3.3) |

Словесный алгоритм метода Ньютона:
- Выбираем начальную точку х. Если
 ,то x=a, иначе x=b.
,то x=a, иначе x=b. - Находим приближение корня (xi+1) по выражению (3.2).
- Итерационный процесс поиска продолжается до тех пор, пока
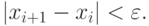
( 3.4)
На основании (3.2) условие (3.4) можно записать как
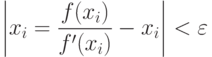
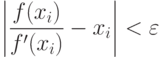
В точке экстремума  производная
производная  меняет знак.
меняет знак.
Если в точке  функция F(x)
имеет минимум, то производная
функция F(x)
имеет минимум, то производная  в окрестности
в окрестности  меняет знак с отрицательного на
положительный, т.е.
меняет знак с отрицательного на
положительный, т.е.  является возрастающей
функцией, значит,
является возрастающей
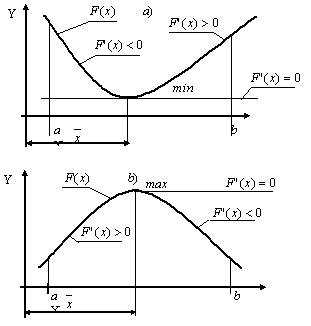
функцией, значит, 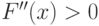 (рис. 9.9 a).
(рис. 9.9 a).
Если в точке  функция F(x)
имеет максимум, то производная
функция F(x)
имеет максимум, то производная  в окрестности
в окрестности  меняет знак с положительного на
отрицательный, т.е.
меняет знак с положительного на
отрицательный, т.е.  является убывающей функцией,
значит,
является убывающей функцией,
значит, 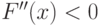 (рис. 9.9 b).
(рис. 9.9 b).
Следовательно, по знаку 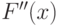 можно судить: в точке
можно судить: в точке  максимум или минимум функции F(x).
максимум или минимум функции F(x).
Если функция F(x) не дифференцируема или вычисление ее производных очень сложно, то для определения производных функции F(x) можно воспользоваться приблизительными оценками производных с помощью разностных схем:
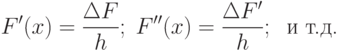
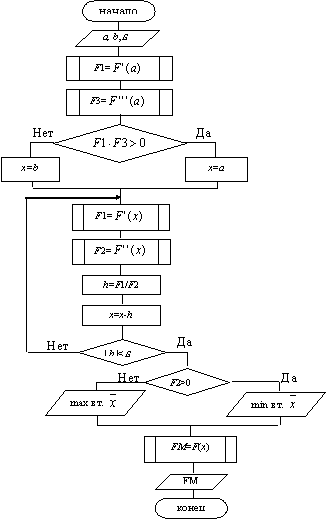
Схема алгоритма метода Ньютона представлена на рис. 9.10.
На рис.9.10:  - координата точки в которой функция F(x) имеет минимальное (или максимальное) значение, FM - значение, функции F(x) в точке
- координата точки в которой функция F(x) имеет минимальное (или максимальное) значение, FM - значение, функции F(x) в точке  .
.