Лекция 8: Задача нелинейного программирования при ограничениях – неравенствах. Седловая точка и задача нелинейного программирования. Применение теоремы Куна – Таккера для задачи выпуклого программирования
Теорема Куна-Таккера. Выше найдены условия оптимальности (1.9), (1.10) для задачи НП с линейными ограничениями. Обобщим эти условия на случай задачи (1.1), (1.2), когда все ограничения нелинейны.
Условия оптимальности решения задачи НП формулируются в следующей теореме, имеющей исключительно важное значение в теории нелинейного программирования.
Теорема 1.1. (Куна-Таккера). Пусть функции 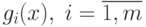 , имеют непрерывные частные производные на
некотором открытом множестве Rn, содержащем точку x+. Если x+ является точкой минимума функции f(x) при ограничениях
, имеют непрерывные частные производные на
некотором открытом множестве Rn, содержащем точку x+. Если x+ является точкой минимума функции f(x) при ограничениях 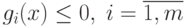 , удовлетворяющих условию регулярности в виде линейной независимости векторов
, удовлетворяющих условию регулярности в виде линейной независимости векторов 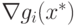 , то существуют такие неотрицательные
множители Лагранжа
, то существуют такие неотрицательные
множители Лагранжа 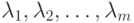 , что
, что
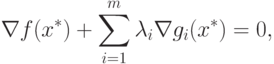 |
( 1.13) |
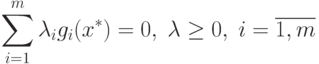 |
( 1.14) |
Определим функцию Лагранжа следующим образом:
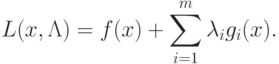 |
( 1.15) |
Тогда теорему Куна-Таккера можно записать в виде
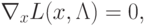 |
( 1.16) |
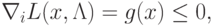 |
( 1.17) |
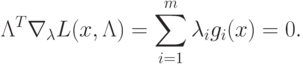 |
( 1.18) |
Заметим, что множители Лагранжа 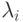 в задаче НП с ограничениями-равенствами
являются знаконеопределенными, тогда как в теореме Куна-Таккера
они должны быть положительными.
в задаче НП с ограничениями-равенствами
являются знаконеопределенными, тогда как в теореме Куна-Таккера
они должны быть положительными.
Доказательство. При достаточно малых t > 0, разлагая f(x++tz) в ряд Тейлора, получим
 |
( 1.19) |

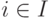 . Заметим, что система неравенств
. Заметим, что система неравенств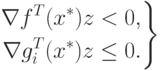 |
( 1.20-1.21) |
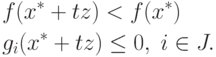
Лемма. При произвольной матрице A выполняется одно из двух условий:
либо выполняется следующая система неравенств:
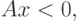 |
( 1.22) |
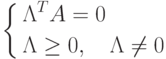 |
( 1.23) |
Применим эту лемму к (1.20), (1.21), приняв за матрицу A
![\left[
\begin{aligned}
& \nabla f (x^*) \\
& \nabla g_i (x^*)
\end{aligned}
\right] , \quad i \in I](/sites/default/files/tex_cache/748a4cd5cce943de12740609054a57ab.png)
Поскольку система (1.20), (1.21) не имеет решений, то существуют такие 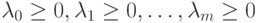 ,
что
,
что
 |
( 1.24) |
![\left[
\begin{aligned}
& \lambda_0 \\
& \lambda_1
\end{aligned}
\right] \neq 0.](/sites/default/files/tex_cache/67bb9234d7d1d58a0c30aede3438ffbf.png)
Если присвоим 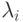 значение 0 для
значение 0 для 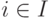 ,
то получим
,
то получим 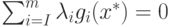 .
Условие
.
Условие 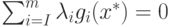 называют условием
дополняющей нежесткости.
называют условием
дополняющей нежесткости.
Покажем, что 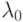 в (1.24) не может равняться 0. В самом деле, если допустить, что
в (1.24) не может равняться 0. В самом деле, если допустить, что  , то получим
, то получим
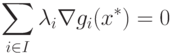 |
( 1.25) |
Однако (1.25) противоречит условию теоремы о линейной независимости
векторов 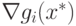 .
Остается принять
.
Остается принять  ..
Тогда, разделив обе части (1.24) на
..
Тогда, разделив обе части (1.24) на 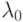 , получим
, получим

Понятие регулярности было впервые введено Г.Куном и А.Таккером
и имеет различные формы. В частном случае, когда все 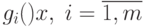 являются выпуклыми функциями, условие
регулярности записывается в
виде: существует такой вектор x, что gi(x)<0 для всех
являются выпуклыми функциями, условие
регулярности записывается в
виде: существует такой вектор x, что gi(x)<0 для всех 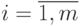 .
Это означает, что может существовать хотя бы одна внутренняя точка
допустимого множества решений. Это условие называют условием регулярности Слейтера.
.
Это означает, что может существовать хотя бы одна внутренняя точка
допустимого множества решений. Это условие называют условием регулярности Слейтера.
