|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема
Некоторые сведения из дифференциальной алгебры
В дифференциальной алгебре рассматриваются алгебраические структуры (кольца,
поля), в которых наряду с арифметическими операциями имеется операция
дифференцирования. При этом дифференцирование определяется не через предельный
переход, а с использованием алгебраических свойств. Типичными объектами, с
которыми
имеет дело дифференциальная алгебра, являются кольца (поля) функций,
определенных на подмножестве вещественной прямой или евклидова пространства
либо на подмножестве комплексной плоскости. В дифференциальной алгебре мы
отвлекаемся от функциональной природы рассматриваемых объектов, не
рассматриваем вопросы области определения функций, однозначности и т. д.,
например, 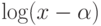 , где
, где  -
алгебраическое число, не
интерпретируется как функция на действительной оси или в области комплексной
плоскости.
-
алгебраическое число, не
интерпретируется как функция на действительной оси или в области комплексной
плоскости.
Прежде всего напомним формальное определение дифференцирования, дифференциального кольца и дифференциального поля (см. определение 3.2).
23.1. ОПРЕДЕЛЕНИЕ.
Отображение  кольца
кольца  в себя называется дифференцированием, дифференцирование если оно удовлетворяет
условиям
в себя называется дифференцированием, дифференцирование если оно удовлетворяет
условиям
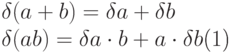 |
( 23.1) |
 .
.23.2. ОПРЕДЕЛЕНИЕ. Обыкновенным дифференциальным кольцом
(полем)
называется кольцо (поле), на котором действует оператор дифференцирования  . Если на кольце (поле) задано несколько попарно
коммутирующих
дифференцирований, то оно называется частным дифференциальным
кольцом полем или кольцом (полем) с частными
производными .
. Если на кольце (поле) задано несколько попарно
коммутирующих
дифференцирований, то оно называется частным дифференциальным
кольцом полем или кольцом (полем) с частными
производными .
В дальнейшем мы ограничимся рассмотрением только обыкновенных дифференциальных полей.
23.3. ПРИМЕРЫ.
- Любое кольцо
 можно рассматривать как дифференциальное
кольцо с
нулевым дифференцированием.
можно рассматривать как дифференциальное
кольцо с
нулевым дифференцированием. - Кольцо бесконечно дифференцируемых на отрезке функций с
дифференцированием по координате
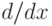 является дифференциальным
кольцом.
является дифференциальным
кольцом. - Кольцо многочленов от одной переменной
 над кольцом
над кольцом  можно
превратить в дифференциальное кольцо, полагая дифференцирование
можно
превратить в дифференциальное кольцо, полагая дифференцирование  тривиальным на
тривиальным на  и произвольным образом задав значение
и произвольным образом задав значение 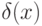 .
Продолжение дифференцирования на все кольцо многочленов определяется однозначно
правилами (23.1).
.
Продолжение дифференцирования на все кольцо многочленов определяется однозначно
правилами (23.1).
23.4. ОПРЕДЕЛЕНИЕ.
Если  - дифференциальное кольцо ( поле ) с
дифференцированием
- дифференциальное кольцо ( поле ) с
дифференцированием  , то
множество элементов
, то
множество элементов 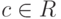 , таких, что
, таких, что 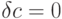 образует подкольцо
(подполе) кольца (поля)
образует подкольцо
(подполе) кольца (поля)  , называемое подкольцом (подполем) констант.
Элемент
, называемое подкольцом (подполем) констант.
Элемент  называется производной элемента
называется производной элемента 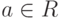 и часто
обозначается
и часто
обозначается 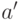 . Элемент
. Элемент 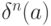 называется
называется  -ой производной
элемента
-ой производной
элемента  и обозначается обычно
и обозначается обычно 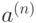 .
.
23.5. ОПРЕДЕЛЕНИЕ.
Пусть 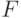 --дифференциальное поле с дифференцированием
--дифференциальное поле с дифференцированием  .
Расширение
.
Расширение 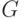 поля
поля 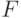 называется дифференциальным расширением
дифференциального поля
называется дифференциальным расширением
дифференциального поля 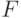 , если на
, если на 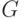 определено
дифференцирование
определено
дифференцирование 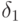 , ограничение которого на
, ограничение которого на 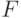 совпадает с
совпадает с  . Дифференцирование
. Дифференцирование 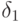 называется продолжением
дифференцирования
называется продолжением
дифференцирования  и
обозначается, если это не приводит к двусмысленности, тем же символом
и
обозначается, если это не приводит к двусмысленности, тем же символом  .
.
Имеют место следующие теоремы о продолжении дифференцирований.
23.6. ТЕОРЕМА.
Пусть  -целостное кольцо,
-целостное кольцо, 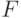 -его поле
частных,
-его поле
частных,  -
дифференцирование кольца
-
дифференцирование кольца  . Тогда дифференцирование
. Тогда дифференцирование  однозначно
продолжается до дифференцирования поля
однозначно
продолжается до дифференцирования поля 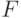 .
.
Нетрудно проверить, что, полагая  , мы получаем нужное продолжение и из соотношения
, мы получаем нужное продолжение и из соотношения  следует единственность этого
продолжения.
следует единственность этого
продолжения.
23.7. ТЕОРЕМА.
Пусть 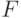 -дифференциальное поле с дифференцированием
-дифференциальное поле с дифференцированием  ,
, 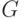 -
алгебраическое расширение поля
-
алгебраическое расширение поля 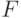 . Тогда дифференцирование
. Тогда дифференцирование  однозначно продолжается до дифференцирования поля
однозначно продолжается до дифференцирования поля 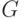 .
.
Действительно, если  удовлетворяет алгебраическому
уравнению
удовлетворяет алгебраическому
уравнению

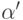 удовлетворяет
соотношению
удовлетворяет
соотношению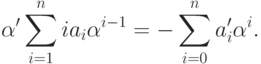
В дифференциальной алгебре логарифмы и экспоненты определяются следующим образом.
23.8. ОПРЕДЕЛЕНИЕ.
Пусть 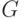 -дифференциальное расширение дифференциального поля
-дифференциальное расширение дифференциального поля 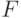 .
Элемент
.
Элемент 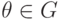 называется логарифмом над
называется логарифмом над 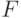 , если
, если  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению  для
некоторого
ненулевого элемента
для
некоторого
ненулевого элемента  (обозначается
(обозначается 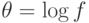 ).
).
23.9. ОПРЕДЕЛЕНИЕ.
Пусть 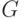 -дифференциальное расширение дифференциального поля
-дифференциальное расширение дифференциального поля 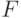 .
Элемент
.
Элемент 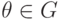 называется экспонентой над
называется экспонентой над 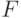 , если
, если  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 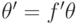 для некоторого
ненулевого элемента
для некоторого
ненулевого элемента  (обозначается
(обозначается  ).
).
Легко видеть, что определяемые в курсе анализа функции 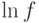 и
и  удовлетворяют этому определению.
удовлетворяют этому определению.
Классической постановкой задачи интегрирования в конечном виде считается
случай, когда 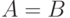 -класс элементарных
функций. Элементарные функции
получаются из рациональных функций посредством арифметических операций и
композиции функций (может быть вложенной) алгебраических, логарифмических и
экспоненциальных. Более строго элементарные функции определяются следующим
образом.
-класс элементарных
функций. Элементарные функции
получаются из рациональных функций посредством арифметических операций и
композиции функций (может быть вложенной) алгебраических, логарифмических и
экспоненциальных. Более строго элементарные функции определяются следующим
образом.
