|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Целозначные многочлены и размерностные многочлены матриц и подмножеств в Nm
12.2. ЛЕММА.
Пусть  и
и  - результат
параллельного сдвига множества
- результат
параллельного сдвига множества  на вектор
на вектор 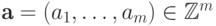 , т.е.
, т.е.  .
Предположим также, что
.
Предположим также, что  .
Тогда для любого
.
Тогда для любого 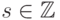 имеем
имеем 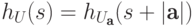 ,
где
,
где 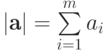 .
.
ДОКАЗАТЕЛЬСТВО.
Очевидно, параллельный сдвиг на вектор  , отображающий точку
, отображающий точку 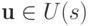 на точку
на точку 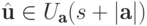 ,
является биективным отображением множеств
,
является биективным отображением множеств 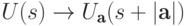 .
Следовательно,
.
Следовательно,
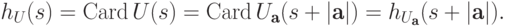
12.3. ЛЕММА.
Пусть  и
и 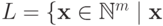 не
превосходит ни одной точки из
не
превосходит ни одной точки из  относительно порядка произведения на
относительно порядка произведения на 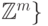 . Тогда существует
подмножество
. Тогда существует
подмножество  , такое, что
, такое, что 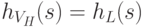 для всех
для всех 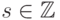 .
.
ДОКАЗАТЕЛЬСТВО.
Для любой точки 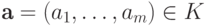 положим
положим 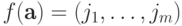 , где
, где  ,
, 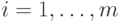 . Пусть
. Пусть  . Тогда
. Тогда 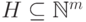 является требуемым множеством. Действительно,
является требуемым множеством. Действительно,  тогда и только тогда, когда
тогда и только тогда, когда 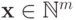 и
и 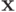 больше или равен некоторой
больше или равен некоторой 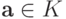 , что эквивалентно неравенству
, что эквивалентно неравенству  ,
,  .
.
Для любого данного подмножества 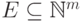 и для
любого элемента
и для
любого элемента 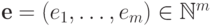 пусть
пусть  и
и 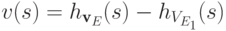 для любого
для любого 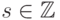 .
Ясно, что
.
Ясно, что  , где
, где  - множество
элементов
- множество
элементов  , таких, что
, таких, что  . Применяя лемму 12.2 к
. Применяя лемму 12.2 к  и
и 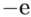 , видим, что
, видим, что 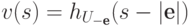 .
Далее, обозначая
.
Далее, обозначая  результат параллельного сдвига
результат параллельного сдвига  на вектор
на вектор 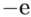 и применяя лемму 12.2, получаем, что
и применяя лемму 12.2, получаем, что  совпадает с
совпадает с 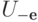 . Таким образом,
. Таким образом, 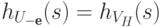 , где множество
, где множество  задается
следующим условием:
задается
следующим условием: 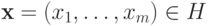 тогда и только тогда, когда существует
элемент
тогда и только тогда, когда существует
элемент  , такой, что
, такой, что  ,
, 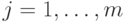 . Таким образом, мы доказали следующую формулу:
. Таким образом, мы доказали следующую формулу:
 |
( 12.1) |
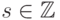 .
.Отметим, что в формуле (12.1) множество  , а
следовательно, и
, а
следовательно, и  , может быть пустым.
, может быть пустым.
12.4. ЛЕММА. Пусть 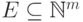
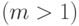 , и
, и 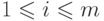 . Предположим, что
. Предположим, что  содержит элемент,
содержит элемент,  -я координата которого равна 1, а все остальные равны 0. Пусть
-я координата которого равна 1, а все остальные равны 0. Пусть 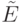 обозначает множество всех элементов
обозначает множество всех элементов  , таких, что
, таких, что  . Тогда
. Тогда  для всех
для всех 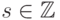 .
.
ДОКАЗАТЕЛЬСТВО.
Отображение 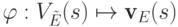 ,
такое, что
,
такое, что
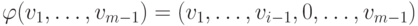
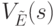 на множество всех элементов
на множество всех элементов 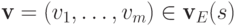 с нулевой
с нулевой  -ой координатой, т.e на множество
-ой координатой, т.e на множество  .
.12.5. ТЕОРЕМА.
Для любого множества 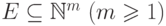 справедливы
следующие утверждения:
справедливы
следующие утверждения:
-
существует целозначный многочлен
 , такой, что
, такой, что  для всех достаточно больших
для всех достаточно больших  ;
; -
 , причем
, причем 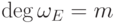 тогда
и только тогда, когда
тогда
и только тогда, когда 
 в этом случае
в этом случае  ;
; -
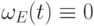 тогда и только тогда, когда
тогда и только тогда, когда  .
.
ДОКАЗАТЕЛЬСТВО.
(1) Очевидно, что если  - множество всех минимальных
элементов множества
- множество всех минимальных
элементов множества  , то
, то  , так что мы можем (и будем) предполагать, что
, так что мы можем (и будем) предполагать, что  конечно и его элементы попарно несравнимы.
Пусть
конечно и его элементы попарно несравнимы.
Пусть 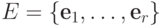 ,
где
,
где 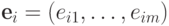
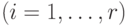 и
пусть
и
пусть 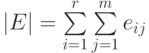 .
Доказательство будем вести индукцией по
.
Доказательство будем вести индукцией по 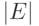 . Если
. Если  , то либо
, то либо  ,
либо
,
либо  состоит из единственного элемента
состоит из единственного элемента 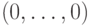 . В первом случае
. В первом случае  и из
(11.22) следует, что
и из
(11.22) следует, что 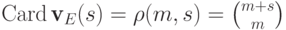 .
Во втором случае (когда
.
Во втором случае (когда  ),
), 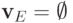 , следовательно,
, следовательно,  для любого
для любого  , так что можно положить
, так что можно положить  .
Таким образом, утверждение (1) доказано при
.
Таким образом, утверждение (1) доказано при  .
.
Более того, если 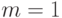 , то
, то  содержит только одну
точку
содержит только одну
точку  , так что
, так что 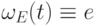 является
требуемым многочленом.
является
требуемым многочленом.
Пусть 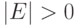 и
и  . Тогда существует отличный от
. Тогда существует отличный от 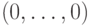 элемент
элемент 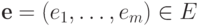 . Пусть
. Пусть  , для некоторого
, для некоторого 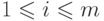 ,
и
,
и 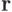 - элемент множества
- элемент множества 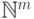 ,
,  -я координата которого равна 1 и все остальные равны 0.
Применяя соотношение (12.1) к
-я координата которого равна 1 и все остальные равны 0.
Применяя соотношение (12.1) к  и
и 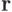 ,
получаем
,
получаем
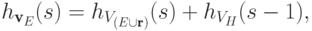
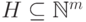 такого, что
такого, что 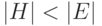 .
.По лемме 12.4  , где
, где  ,
,  .
Согласно индуктивному предположению можно считать, что существуют
целозначные многочлены
.
Согласно индуктивному предположению можно считать, что существуют
целозначные многочлены 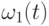 и
и 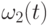 такие,
что
такие,
что  и
и  для всех достаточно больших
для всех достаточно больших 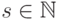 . Поэтому
целозначный многочлен
. Поэтому
целозначный многочлен
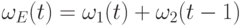
(2) Как мы уже видели, если  ,
то
,
то  ,
, 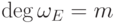 . Значит, чтобы
доказать второе утверждение теоремы,
достаточно доказать, что
. Значит, чтобы
доказать второе утверждение теоремы,
достаточно доказать, что 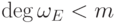 , если
, если 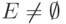 .
Формула (12.1), примененная в случае пустого множества
.
Формула (12.1), примененная в случае пустого множества  и
произвольного вектора
и
произвольного вектора  ,
показывает, что
,
показывает, что

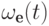 является многочленом степени
является многочленом степени 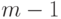 .
Остается отметить, что добавление новых элементов в
множество
.
Остается отметить, что добавление новых элементов в
множество  может только уменьшить
значения
может только уменьшить
значения  , а, следовательно, не может увеличить степень
многочлена
, а, следовательно, не может увеличить степень
многочлена 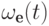 .
.(3) Как мы уже видели, 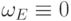 ,
если
,
если  . С другой стороны,
если
. С другой стороны,
если 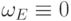 , то
, то 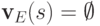 для всех
достаточно больших
для всех
достаточно больших  , следовательно,
, следовательно, 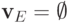 .
.
