НОУ ИНТУИТ | Введение в компьютерную алгебру. Лекция 3: Наибольший общий делитель и последовательности полиномиальных остатков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 04.03.2008 | Доступ: свободный | Студентов: 1635 / 50 | Оценка: 4.56 / 3.67 | Длительность: 30:07:00

ISBN: 978-5-9556-0099-4

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Алгоритм примитивных PRS

В этом случае

$\beta_i=\cont\{\prem[p_i(x),p_{i+1}(x)]\},\quad i=1, 2,\dots , h-1,$

где prem обозначает псевдоостаток, т. е. теперь мы удаляем содержание (i + 2) -го члена PRS до того, как мы используем его. [Напомним, что для данного p(x) удобно определять p. p.[p(x)] так, чтобы старший коэффициент был положительным.]

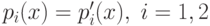6.6. ПРИМЕР. Рассмотрим те же полиномы, что и в предыдущем примере: p₁(x) = x³ - 7x + 7, p₂(x) = 3x² - 7 в $\mathbb Z[x]$ , где снова $p_i(x)=p'_i(x) , \; i=1,2$ Теперь мы получаем

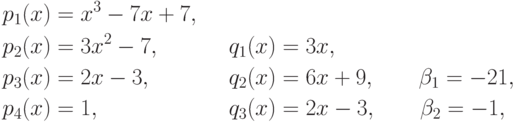
$\begin{align*} {}&p_1(x)=x^3-7x+7, &\quad& \\ {}&p_2(x)=3x^2-7, &&q_1(x)=3x,\\ {}&p_3(x)=2x-3, &&q_2(x)=6x+9,\qquad \beta_1=-21,\\ {}&p_4(x)=1, &&q_3(x)=2x-3,\qquad \beta_2=-1, \end{align*}$

что достигается выполнением следующих псевдоделений:

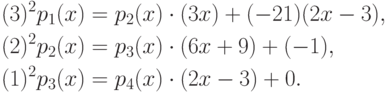
$\begin{align*} (3)^2p_1(x)&=p_2(x)\cdot(3x)+(-21)(2x-3),\\ (2)^2p_2(x)&=p_3(x)\cdot(6x+9)+(-1),\\ (1)^2p_3(x)&=p_4(x)\cdot(2x-3)+0. \end{align*}$

Этот алгоритм дает наилучшие возможные результаты в отношении роста коэффициентов, однако, они достигаются достаточно сложными вычислениями НОД коэффициентов на каждом этапе. В монографии [ 7 ] , 2.3.3] утверждается, что лучшим из известных методов вычисления НОД многочленов, основанных на применении к многочленам с целыми коэффициентами алгоритма Евклида, является метод, в котором множители 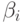$\beta _{i}$ выбираются следующим образом.

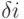Предположим, что даны два многочлена $p_1(x), p_2(x) \in \mathbb Z[x]$ . Для вычисления их НОД построим последовательность полиномиальных остатков p₃(x), p₄(x), . . . , p_s(x), 0. Введем обозначение c_i для старшего коэффициента многочлена pi(x) и $\delta i$ для разности степеней многочленов p_i(x) и p_i+1(x). Последовательность полиномиальных остатков строим по формуле (6.1), в которой полагаем

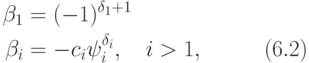
$\begin{aligned} {\beta_1&=(-1)^{\delta_1+1}\\ \beta_i&=-c_i\psi_i^{\delta_i},\quad i>1,} \quad \quad \quad \ecno(6.2) \end{aligned}$

где

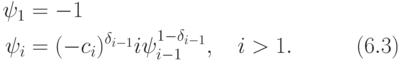
$\begin{aligned} \psi_1&=-1 \\ \psi_i&=(-c_i)^{\delta_{i-1}}i\psi_{i-1}^{1-\delta_{i-1}},\quad i>1.\quad \quad \quad \ecno(6.3) \end{aligned}$

Теорема о субрезультантах (см., например, [ 12 ] ) утверждает, что все p_i являются многочленами с целыми коэффициентами.

6.7. ПРИМЕР. Анализ вычисления НОД следующих многочленов выполнен Брауном [ 17 ] . Этот пример разобран также в монографии [ 7 ] , § 2.3.3].

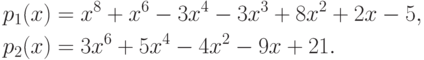
$\begin{align*} p_1(x)&=x^8+x^6-3x^4-3x^3+8x^2+2x-5,\\ p_2(x)&=3x^6+5x^4-4x^2-9x+21. \end{align*}$

Рассматривая эти многочлены как элементы кольца $\mathbb Q[x]$ и применяя алгоритм Евклида, мы получаем следующую последовательность:

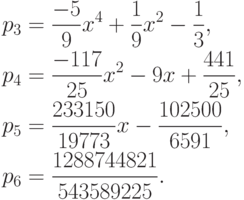
$\begin{align*} p_3&=\frac{-5}9x^4+\frac19x^2-\frac13,\\ p_4&=\frac{-117}{25}x^2-9x+\frac{441}{25},\\ p_5&=\frac{233150}{19773}x-\frac{102500}{6591},\\ p_6&=\frac{1288744821}{543589225}. \end{align*}$

Все выписанные дроби являются несократимыми.

Выписанная последовательность достаточно трудоемка для вычислений вручную. Рекомендуется воспользоваться системой компьютерной алгебры Maple. Данная последовательность полиномиальных остатков получается с помощью функции rem, вычисляющей остатки. По умолчанию система Maple не упорядочивает слагаемые в многочленах, для этой цели используется функция sort. Последовательность команд может выглядеть следующим образом:

$\begin{verbatim} p[1]:=x^8+x^6-3*x^4-3*x^3+8*x^2+2*x-5; p[2]:=3*x^6+5*x^4-4*x^2-9*x+21; p[3]:=sort(rem(p[1],p[2],x)); p[4]:=sort(rem(p[2],p[3],x)); p[5]:=sort(rem(p[3],p[4],x)); p[6]:=sort(rem(p[4],p[5],x)); \end{verbatim}$

Применение нормализации делителя позволяет уменьшить коэффициенты, но не слишком сильно.

Для данного примера евклидова последовательность полиномиальных остатков имеет вид

$\begin{align*} p_3&=-15x^4+3x^2-9,\\ p_4&=15795x^2+30375x-59535,\\ p_5&=1254542875143750x-1654608338437500,\\ p_6&=12593338795500743100931151992187500. \end{align*}$

Для вычисления этой последовательности с помощью системы Maple нужно в приведенной выше программе заменить функцию rem на prem.

Наконец, применяя формулы (6.2) и (6.3), мы получаем последовательность

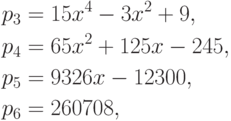
$\begin{align*} p_3&=15x^4-3x^2+9,\\ p_4&=65x^2+125x-245,\\ p_5&=9326x-12300,\\ p_6&=260708, \end{align*}$

которая возрастает значительно медленнее, чем предыдущие последовательности.

Дальше >>

Авторизоваться

Введение в компьютерную алгебру

Наибольший общий делитель и последовательности полиномиальных остатков

Алгоритм примитивных PRS

Вопросы и ответы