|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Лекция 10: Алгоритмы факторизации, основанные на выборе малого вектора в решетке
Обсуждение алгоритма
Отметим, что введенные выше константы  ,
,  и
и  можно вычислять не для
максимально возможной степени делителя многочлена
можно вычислять не для
максимально возможной степени делителя многочлена  , т.е.
, т.е. 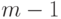 , а для
текущей степени
, а для
текущей степени  . При этом точность вычислений на
промежуточных этапах
понизится, соответственно скорость счета увеличится, кроме того с большой
вероятностью нам не придется считать до максимального значения
. При этом точность вычислений на
промежуточных этапах
понизится, соответственно скорость счета увеличится, кроме того с большой
вероятностью нам не придется считать до максимального значения  .
Так будет,
если неприводимый множитель, соответствующий корню
.
Так будет,
если неприводимый множитель, соответствующий корню  ,
имеет степень
меньше, чем
,
имеет степень
меньше, чем 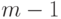 . С учетом этого замечания и
использованием алгоритма
редуцирования базиса решетки вышеприведенный алгоритм принимает вид:
. С учетом этого замечания и
использованием алгоритма
редуцирования базиса решетки вышеприведенный алгоритм принимает вид:
А39. АЛГОРИТМ (выделить-неприводимый-множитель).
![\begin{equation*}
\text{Дано:\quad $f(x) \in \mathbb Z [x], deg f(x) = m$}\\
\text{Надо:\qquad $g(x) \in \mathbb Z [x],\g(x)$ неприводим в $\mathbb Z [x]$}\\
\text{Переменные:\quad решетка $L$}\\
\text{Начало}\\
\text{вычислить начальное приближение $\tilde\alpha$ корня $\alpha$ и }\\
\text{ значение $S$, такое, что в шаре с центром $\tilde\alpha$} \\
\text{радиуса $S$ содержится ровно один корень многочлена $f$}}\\
\text{$L$.базис$[0] := 1$}\\
\text{успех := "нет"}\\
\text{цикл для $n$ от $1$ до $m-1$ пока не успех}\\
\text{\qquad $L$.базис$[n] := x^n$}\\
\text{\qquad минимальный многочлен ($L$, успех)}\\
\text{конец цикла}\\
\text{если успех то}\\
\text{\qquad $g(x) := L$.базис$[0]$}\\
\text{иначе}\\
\text{\qquad $g(x) := f(x)$}\\
\text{конец если}\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/acb9a30e9fabde75c09c93c2bb32545d.png)
21.5. p-адическая метрика.
Переходим к подробному изложению алгоритма факторизации многочленов
от одной переменной, основанному на использовании  - адической метрики и построении редуцированного базиса
решетки.
Предполагаем, что мы нашли неприводимый по модулю некоторого
простого числа
- адической метрики и построении редуцированного базиса
решетки.
Предполагаем, что мы нашли неприводимый по модулю некоторого
простого числа  множитель многочлена
множитель многочлена ![f(x) \in
\mathbb Z [x]](/sites/default/files/tex_cache/0b46fdc7b40962692c4f62f5ca41041e.png) , и что мы подняли
этот неприводимый множитель до некоторого множителя
, и что мы подняли
этот неприводимый множитель до некоторого множителя 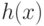 , делящего многочлен
, делящего многочлен  по модулю некоторой
степени числа
по модулю некоторой
степени числа  .
Предположим также, что старший коэффициент многочлена
.
Предположим также, что старший коэффициент многочлена 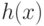 равен 1 и что многочлен
равен 1 и что многочлен  не делится на
не делится на 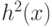 по модулю
по модулю  .
Таким образом, предполагаем, что
.
Таким образом, предполагаем, что
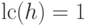 |
( 21.16) |
![{}&(h\mod{p^k})\text{ делит } (f\mod p^k )\text{ в }(\mathbb Z /p^k
\mathbb Z )[x]](/sites/default/files/tex_cache/10e4ab86481cd8442e476b952b33d287.png) |
( 21.17) |
![{}&(h\mod p)\text{ неприводим в } F_p[x]](/sites/default/files/tex_cache/f233f8c51024f34411660e86af72dd27.png) |
( 21.18) |
![{}&(h\mod p)^2\text{ не делит }(f\mod p)\text{ в кольце }F_p[x]](/sites/default/files/tex_cache/465db567605ab10a24201031d1338fd9.png) |
( 21.19) |
Положим  , тогда
, тогда 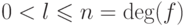 .
.
Покажем, что множество многочленов ![g(x) \in
\mathbb Z [x]](/sites/default/files/tex_cache/98c82f5870ca8f1c1d694d049c4be9cf.png) , которые делятся по модулю
, которые делятся по модулю  на многочлен
на многочлен 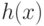 , образуют в
, образуют в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) главный идеал, порожденный
некоторым неприводимым множителем
главный идеал, порожденный
некоторым неприводимым множителем  многочлена
многочлена  .
.
Другими словами, пусть 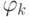 обозначает естественный
гомоморфизм
кольца
обозначает естественный
гомоморфизм
кольца ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) на факторкольцо
на факторкольцо ![(\mathbb Z /p^k \mathbb Z )[x]](/sites/default/files/tex_cache/1f818187379714e778610e5fd65a4ab1.png) , ядро
гомоморфизма
, ядро
гомоморфизма 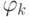 совпадает с главным идеалом
совпадает с главным идеалом 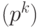 кольца
кольца ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) ,
, 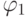 обозначим просто
обозначим просто  . Пусть
. Пусть  - главный идеал кольца
- главный идеал кольца ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) , порожденный
многочленом
, порожденный
многочленом  , удовлетворяющим
условиям (21.16)-(21.19). Тогда существует
, удовлетворяющим
условиям (21.16)-(21.19). Тогда существует ![h_0 \in
\mathbb Z [x]](/sites/default/files/tex_cache/c02da264f05bbb389b03682a6559c70b.png) , такой, что при любом
, такой, что при любом  в
в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) совпадают идеалы
совпадают идеалы 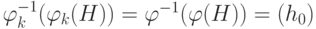 . Многочлен
. Многочлен 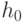 является неприводимым в
является неприводимым в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) и делит
и делит  .
.
21.3. ПРЕДЛОЖЕНИЕ.
Существует неприводимый в кольце ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) множитель
множитель  многочлена
многочлена  ,
для которого
,
для которого  делит
делит  , и этот
множитель определен однозначно с точностью до
знака. Кроме того, если
, и этот
множитель определен однозначно с точностью до
знака. Кроме того, если ![g(x) \in \mathbb Z [x]](/sites/default/files/tex_cache/9ef0c26c409ad956e524603dbe268274.png) и
и 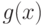 делит
делит  , то следующие условия эквивалентны.
, то следующие условия эквивалентны.
![{}&(h\mod p)\text{ делит }(g\mod p)\text{ в кольце }F_p[x]](/sites/default/files/tex_cache/150bf6f1794d05ba77f2ae582a19a3b3.png) |
( 21.20) |
![{}&(h\mod p^k )\text{ делит }(g\mod p^k )\text{ в кольце }(\mathbb Z /p^k
\mathbb Z )[x]](/sites/default/files/tex_cache/2fe329b461d1069c8c74f9903e3d07e1.png) |
( 21.21) |
![{}&h_0\text{ делит }g\text{ в кольце }\mathbb Z [x]](/sites/default/files/tex_cache/8fd03ad3d390e9777ecf1fabab396a83.png) |
( 21.22) |
В частности,  делит
делит  в
кольце
в
кольце ![(\mathbb Z /p^k\mathbb Z )[x]](/sites/default/files/tex_cache/4cc8c68d0c5e55d3a4ca907693d43eee.png) . В теоретико-кольцевых терминах
эти условия переписываются следующим образом:
. В теоретико-кольцевых терминах
эти условия переписываются следующим образом:
![{}&\varphi(g) \in ( \varphi(h)) \subset F_p[x]](/sites/default/files/tex_cache/7d4ffbea34f315d27191d6334ecd0a47.png) |
( 21.20') |
![{}&\varphi_k (g) \in ( \varphi_k (h)) \subset (\mathbb Z /p^k \mathbb Z )[x]](/sites/default/files/tex_cache/aabe79edc398cf706bf19fa9a3e6a519.png) |
( 21.21') |
![{}&g \in (h_0 ) \subset \mathbb Z [x]](/sites/default/files/tex_cache/cf2759146ba33cea6dcb4de495231e76.png) |
( 21.22') |
В частности,
![\begin{equation*}
\varphi_k (h_0 ) \in (\varphi_k (h)) \subset (\mathbb Z /p^k \mathbb Z )[x]
\end{equation*}](/sites/default/files/tex_cache/5d2464c52b08f8df19276799865d8ed2.png)
ДОКАЗАТЕЛЬСТВО.
Существование многочлена 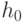 следует из того, что
следует из того, что 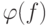 делится на
делится на  . Поскольку
многочлен
. Поскольку
многочлен  неприводим, на него делится
неприводим, на него делится 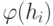 хотя бы для
одного из неприводимых делителей
хотя бы для
одного из неприводимых делителей 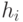 многочлена
многочлена  , а
так как эти
делители взаимно просты, то делится в точности один из них.
, а
так как эти
делители взаимно просты, то делится в точности один из них.
Поскольку  является кольцевым гомоморфизмом, и
разлагается в
композицию гомоморфизмов
является кольцевым гомоморфизмом, и
разлагается в
композицию гомоморфизмов 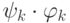 , где
, где 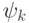 -
естественный гомоморфизмом кольца
-
естественный гомоморфизмом кольца ![\mathbb Z /p^k \mathbb Z [x] \to F_p[x]](/sites/default/files/tex_cache/b974c68a68e4ae0a56188602ae52cf93.png) , как из
(21.22), так и из (21.21) следует (21.20).
, как из
(21.22), так и из (21.21) следует (21.20).
Покажем, что из (21.20) следует (21.21) и (21.22).
Пусть выполнено условие (21.20).
Тогда 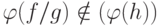 в силу (21.19) и
однозначности
разложения на множители в
в силу (21.19) и
однозначности
разложения на множители в ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png) . Значит,
. Значит, 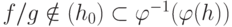 . Из
однозначности
разложения на множители в
. Из
однозначности
разложения на множители в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) следует, что
следует, что  , т.е. выполнено
(21.22).
, т.е. выполнено
(21.22).
Пусть снова выполнено условие (21.20). Поскольку ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png) является областью главных идеалов, из (21.20) следует, что
существуют
является областью главных идеалов, из (21.20) следует, что
существуют ![u(x),v(x) \in F_p[x]](/sites/default/files/tex_cache/8224a74473fd0c0dec6e1c8c19486237.png) , такие, что
, такие, что 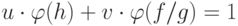 в
в ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png) . Поскольку
. Поскольку  -
эпиморфизм, ядро которого порождено числом
-
эпиморфизм, ядро которого порождено числом  , выписанное
соотношение можно поднять до равенства в кольце
, выписанное
соотношение можно поднять до равенства в кольце ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png)
 |
( 21.23) |
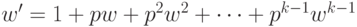 .
Применяя
.
Применяя 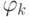 к предыдущему соотношению, умноженному на
к предыдущему соотношению, умноженному на 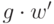 ,
получим
,
получим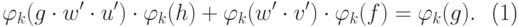 |
( 21.24) |
Из этого соотношения и (21.17) следует (21.21).
