|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы вычисления размерностных многочленов
13.8. ПРИМЕР.
Найдем значение 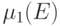 для
матрицы
для
матрицы
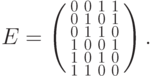
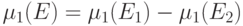 ,
где
,
где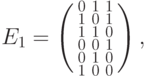
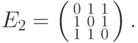
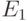 являются
"лишними", поэтому
являются
"лишними", поэтому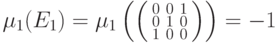
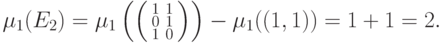 Следовательно,
Следовательно, 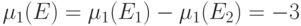 .
.Другой метод вычисления 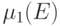 основан на лемме 13.7:
основан на лемме 13.7:
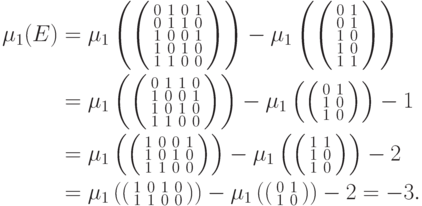
В качестве следствия леммы 13.7 получаем следующее утверждение, на котором основан алгоритм вычисления размерностного многочлена матрицы (см. ниже алгоритм A11 ).
13.9. ЛЕММА.
Пусть 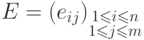 -
- 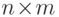 -матрица над
-матрица над 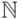 и
и 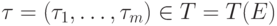 (как и выше,
(как и выше, 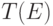 обозначает множество всех допустимых
векторов матрицы
обозначает множество всех допустимых
векторов матрицы  , т. е. множество всех элементов
, т. е. множество всех элементов 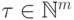 , равных либо
, равных либо 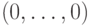 , либо наименьшему общему
кратному некоторых строк
матрицы
, либо наименьшему общему
кратному некоторых строк
матрицы  ). Пусть
). Пусть  - матрица, состоящая из всех
тех строк матрицы
- матрица, состоящая из всех
тех строк матрицы  , которые мажорируются
вектором
, которые мажорируются
вектором  (для определенности
предположим, что строки матрицы
(для определенности
предположим, что строки матрицы  располагаются в том же порядке, в
каком они
расположены в матрице
располагаются в том же порядке, в
каком они
расположены в матрице  ). Кроме того, пусть
). Кроме того, пусть 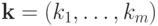 - одна из строк
матрицы
- одна из строк
матрицы  и
и 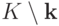 - матрица, полученная
удалением строки
- матрица, полученная
удалением строки  из
из  . Тогда для любого
подмножества
. Тогда для любого
подмножества 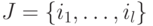 множества
множества 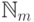 , такого,
что
, такого,
что 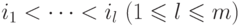 , имеем
, имеем
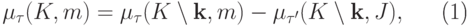 |
( 13.6) |
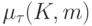 ,
, 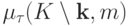 суть
соответственно коэффициенты
суть
соответственно коэффициенты 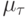 , определенные формулой
(13.2) для матриц
, определенные формулой
(13.2) для матриц  и
и 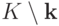 ,
а
,
а  - аналогичные коэффициенты
для
вектора
- аналогичные коэффициенты
для
вектора  (вместо
(вместо  ) и для
) и для 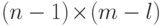 -матрицы, полученной из
-матрицы, полученной из  удалением столбцов с индексами
удалением столбцов с индексами  .
.ДОКАЗАТЕЛЬСТВО.
Без потери общности можно предположить, что  - первая
строка матрицы
- первая
строка матрицы  . Из леммы 13.1 следует, что
. Из леммы 13.1 следует, что
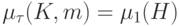
 -
- 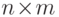 -матрица
с элементами
-матрица
с элементами 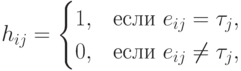
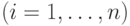 .
Аналогично,
.
Аналогично,  и
и 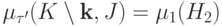 ,
где матрица
,
где матрица 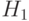 получена из
получена из  отбрасыванием первой
строки,
а
отбрасыванием первой
строки,
а 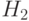 получена из
получена из 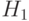 отбрасыванием столбцов с
индексами
отбрасыванием столбцов с
индексами 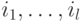 . Применяя теперь лемму 13.7, получаем соотношение
. Применяя теперь лемму 13.7, получаем соотношение  , из которого следует требуемое утверждение.
, из которого следует требуемое утверждение.Вычисление коэффициентов 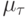
 в (13.4) для
размерностного многочлена произвольной
в (13.4) для
размерностного многочлена произвольной 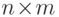 -матрицы
-матрицы  (а, значит,
и вычисление самого размерностного многочлена) может быть выполнено по
следующей схеме: сначала применяем (13.6) к
матрице
(а, значит,
и вычисление самого размерностного многочлена) может быть выполнено по
следующей схеме: сначала применяем (13.6) к
матрице  (формируя
матрицу
(формируя
матрицу  тех строк матрицы
тех строк матрицы  , которые мажорируются
вектором
, которые мажорируются
вектором  . Ясно,
что коэффициенты
. Ясно,
что коэффициенты 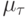 для
матриц
для
матриц  и
и  совпадают). Затем вычисляем
значения
совпадают). Затем вычисляем
значения 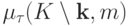 и
и  , снова
применяя (13.6) и т. д., пока не получим "пустые" матрицы (т. е.
матрицы с нулевым числом строк).
, снова
применяя (13.6) и т. д., пока не получим "пустые" матрицы (т. е.
матрицы с нулевым числом строк).

Чтобы оценить асимптотическую сложность алгоритма A11 для достаточно больших 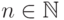 ,
заметим, прежде всего, что при фиксированном векторе
,
заметим, прежде всего, что при фиксированном векторе 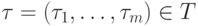 построение
построение 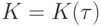 требует не
более
требует не
более 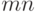 сравнений чисел (на этом шаге мы запоминаем все
пары
сравнений чисел (на этом шаге мы запоминаем все
пары  , для которых
, для которых  ). Далее, выполнение элементарных операций
для всех вызовов алгоритма NEXTINDEX (для
фиксированного
). Далее, выполнение элементарных операций
для всех вызовов алгоритма NEXTINDEX (для
фиксированного  ) требует не более
) требует не более 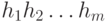 сравнений, где
сравнений, где 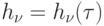
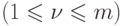 обозначает число
строк
обозначает число
строк 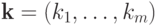 матрицы
матрицы  , таких,
что
, таких,
что  для всех
для всех 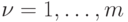 . Легко
видеть, что общее число операций для всех вызовов
алгоритма NEXTINDEX (с точностью до постоянного множителя это число
равно
. Легко
видеть, что общее число операций для всех вызовов
алгоритма NEXTINDEX (с точностью до постоянного множителя это число
равно 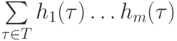 ) не
превосходит
) не
превосходит  для каждого
для каждого 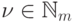 существует
существует 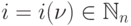 , такое, что
, такое, что 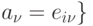 , и это не
превосходит
, и это не
превосходит 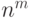 .
Поэтому для достаточно больших
.
Поэтому для достаточно больших 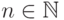 асимптотическая сложность
алгоритма A11 имеет
порядок
асимптотическая сложность
алгоритма A11 имеет
порядок 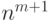 .
.

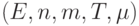 .
.