|
как проверить себя, выполняя практические задания по информатике? где смотреть ответы на поставленные задачи? спасибо за ответ) |
Кабардино-Балкарский государственный университет
Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 2679 / 732 | Оценка: 4.21 / 4.22 | Длительность: 03:26:00
Тема: Образование
Специальности: Программист
Практическая работа 5:
Высказывания и предикаты
< Практическая работа 4 || Практическая работа 5 || Самостоятельная работа 1 >
Аннотация: Решение типовых задач алгебры высказываний и предикатов, обучение реферированию и Интернет–поиску по этой теме
Ключевые слова: предикат, логическая функция, упрощение логического выражения, логическое выражение, отрицание, высказывание, эквивалентность
Задачи
- Определить множество истинности предиката р(х)="число х кратно 4", x?[1;10]. Нарисовать множества истинности и ложности этого предиката. Указание: условие кратности означает, что нужно рассматривать только натуральные числа из этого промежутка, поэтому область определения предиката – X={1,2,3,4,5,6,7,8,9,10}.
- Определить множество истинности предиката p(x,y)= "число х равно числу y", x, y?[3;6]. Нарисовать множества истинности и ложности этого предиката. Указание: множество состоит из пар чисел; условие кратности означает, что нужно рассматривать только натуральные числа из этого промежутка, т.е. x, y=3, 4, 5, 6.
- Запишите предикат (условие, которое может быть и сложным), полностью описывающий область, строго заключенную между окружностями с центром в начале координат и радиусами 3 и 5 соответственно. Указание: сделать вначале рисунок.
- Составить таблицу истинности функции
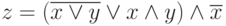 . Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции. Указание: "шапка" таблицы содержит выражения (столбцы) x, y, x?y, x?y,
. Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции. Указание: "шапка" таблицы содержит выражения (столбцы) x, y, x?y, x?y,  ,
, 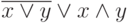 ,
,  , z.
, z. - Дано выражение:
 . Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции. Указание: использовать аксиому де Моргана два раза.
. Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции. Указание: использовать аксиому де Моргана два раза. - Дано выражение:
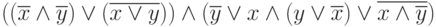 . Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции. Указание: в первой из перемножаемых скобок слагаемые равны.
. Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции. Указание: в первой из перемножаемых скобок слагаемые равны. - Подобрать две функции, эквивалентные данной функции, но с меньшим числом операций и операндов:
 . Указание: под внутренним знаком отрицания применить аксиому поглощения.
. Указание: под внутренним знаком отрицания применить аксиому поглощения. - Из указанных ниже функций отметить (с обоснованием) эквивалентные между собой функции:
-
 ;
; 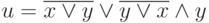
-
 .
.
-
- Из указанных ниже функций отметьте (с обоснованием) эквивалентные между собой функции:
-
 ;
; -
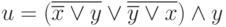 ;
; -
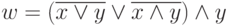 ;
; -
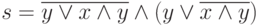 ;
; -
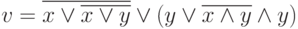 .
.
-
- Построить таблицы истинности для всех функций предыдущей задачи. Указание: построить таблицы для исходных выражений, определив "шапки" каждой таблицы.
Темы научных исследований и рефератов (Интернет-листов)
- История развития алгебры высказываний и предикатов.
- Джордж Буль и его алгебра.
- Примеры алгебр Буля.
- Алгебра множеств (Кантора) – как алгебра Буля.
- Алгебра отношений (реляционная алгебра), его значение и приложения.
- Алгебра логики – как теории доказательств и рассуждений.
- Развитие логических систем (учений) от Аристотеля.
- Тавтологии, силлогизмы и парадоксы.
- Эквивалентность логических функций.
- Логика и ее использование при доказательстве прямых, обратных и противоположных утверждений.
< Практическая работа 4 || Практическая работа 5 || Самостоятельная работа 1 >
