Численные методы решения экстремальных задач
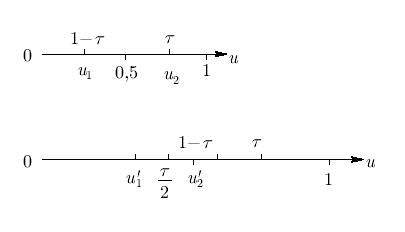
Пусть  тогда симметрично расположенная относительно центра отрезка точка имеет координату
тогда симметрично расположенная относительно центра отрезка точка имеет координату  (рис. 4.1).
(рис. 4.1).
Пробная точка u1 отрезка [0, 1] перейдет в пробную точку 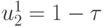 нового отрезка
нового отрезка ![[0, \tau ].](/sites/default/files/tex_cache/1e1c0a7fdfec215cbb2a0a4157e8a501.png) Условием деления отрезков [0, 1] и
Условием деления отрезков [0, 1] и ![[0, \tau ]](/sites/default/files/tex_cache/65d06ef289e35430c4645b0a7a9f4a21.png) в одном и том же отношении точками
в одном и том же отношении точками 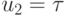 и
и 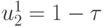 является равенство
является равенство
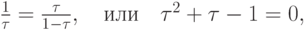
откуда находим положительный корень
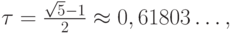
т.е.
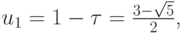

Для отрезка [a, b]
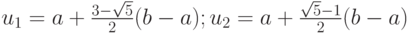
Замечания.
- Точки u1, u2 обладают следующим свойством: каждая из них делит отрезок [a, b] на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей части. Точки, обладающие таким свойством, называются точками золотого сечения, введенного Леонардо да Винчи.
- На каждой итерации отрезок поиска минимума уменьшается в одном и том же
отношении

поэтому в результате n итераций длина становиться равной
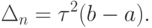
Следовательно, точность
 определения точки u* после n итераций равна
определения точки u* после n итераций равна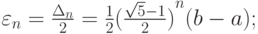
а условие окончания вычислительного процесса будет

Метод парабол.
Методы, использующие исключение отрезков, основаны на сравнении функций в двух точках пробного отрезка, учитываются лишь значения функции в этих точках.
Учесть информацию о значениях функции между точками позволяют методы полиномиальной аппроксимации. Их основная идея заключена в том, что функция 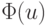 аппроксимируется полиномом, а точка его минимума служит приближением к u*. Разумеется, в этом случае кроме свойства унимодальности (т.е. наличия единственного минимума на рассматриваемом отрезке), необходимо на
аппроксимируется полиномом, а точка его минимума служит приближением к u*. Разумеется, в этом случае кроме свойства унимодальности (т.е. наличия единственного минимума на рассматриваемом отрезке), необходимо на 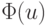 наложить и требования достаточной гладкости для ее полиномиальной аппроксимации.
наложить и требования достаточной гладкости для ее полиномиальной аппроксимации.
Для повышения точности поиска u* можно как увеличивать степень полинома, так и уменьшать пробный отрезок. Поскольку первый прием приводит к заметному увеличению вычислительной работы и появлению дополнительных экстремумов, обычно пользуются полиномами второй ( метод парабол ) или третьей (метод кубической интерполяции) степени.
Алгоритм поиска минимума состоит в следующем.
Выбираем на пробном отрезке три точки u1, u2, u3 такие, что u1 < u2 < u3 и 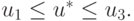
Построим параболу (квадратичный полином)
Q(u) = a0 + a1 (u - u1) + a2 (u - u1)(u - u2),
график которой проходит через точки (u1,f(u1)), (u2,f(u2)), (u3,f(u3)).
Коэффициенты ak, k = 1, 2, 3 находим из системы уравнений
Q(u1) = f(u1), Q(u2) = f(u2), Q(u3) = f(u3),
откуда
![\begin{gather*}
a_0 = f(u_1), a_1 = \frac{f(u_2) - f(u_1)}{u_2 - u_1}, \\
a_2 = \frac{1}{u_3 - u_2} \left[{\frac{f(u_3) - f(u_1)}{u_3 - u_1} - \frac{f(u_2) - f(u_1)}{u_2 - u_1}}\right].
\end{gather*}](/sites/default/files/tex_cache/f90641f1d08c06d45f2cce593ec5ea55.png)
Точку 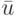 минимума Q(u) находим, приравнивания его производную к нулю:
минимума Q(u) находим, приравнивания его производную к нулю:
![\begin{gather*}
\bar u = \frac{1}{2}(u_1 + u_2 - \frac{a_1}{a_2}) = \\
= \frac{1}{2} \left[{(u_1 + u_2) - \frac{(f_2 - f_1)(u_3 - u_2)}{u_2 - u_1}/(\frac{f_3 - f_1}{u_3 - u_1} - \frac{f_2 - f_1}{u_2 - u_1})}\right].
\end{gather*}](/sites/default/files/tex_cache/930e7ef5cdbb839ab6556365f666f838.png)
Далее полагаем: 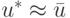 (очередное приближение точки минимума). Эту процедуру можно продолжить до достижения необходимой точности, выбирая новые точки uk, k = 1, 2, 3. Для этого можно использовать методы исключения отрезков, используя в качестве двух пробных точек u2 и
(очередное приближение точки минимума). Эту процедуру можно продолжить до достижения необходимой точности, выбирая новые точки uk, k = 1, 2, 3. Для этого можно использовать методы исключения отрезков, используя в качестве двух пробных точек u2 и 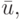 таких, что u2,
таких, что u2, ![\bar u \in [u_1,u_3].](/sites/default/files/tex_cache/f9f4f56d6481ece7134192b6e0963e72.png)