| Россия, Новосибирск |
Схемы из функциональных элементов
Теорема 13. Существует схема умножения двух  -разрядных
чисел размера
-разрядных
чисел размера  и глубины
и глубины 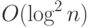 .
.
Начнем с такого замечания. Вычисляя произведение двух комплексных чисел
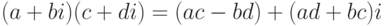
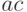 ,
, 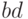 и
и 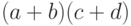 , а потом найти
, а потом найти  как разность
как разность 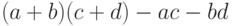 .
.Аналогичный фокус можно проделать и для целых чисел. Разобьем  -битовое число на две
-битовое число на две  -битовые части, то есть
представим его в виде
-битовые части, то есть
представим его в виде 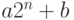 . Теперь запишем произведение двух таких чисел:
. Теперь запишем произведение двух таких чисел:

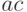 ,
, 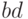 и
и 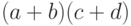 , чтобы определить
все три слагаемых в правой части равенства.
Получается, что умножение двух
, чтобы определить
все три слагаемых в правой части равенства.
Получается, что умножение двух  -разрядных чисел сводится
к трем умножениям
-разрядных чисел сводится
к трем умножениям  -разрядных и к нескольким сложениям и
вычитаниям. (На самом деле при умножении
-разрядных и к нескольким сложениям и
вычитаниям. (На самом деле при умножении  на
на 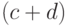 сомножители могут быть
сомножители могут быть 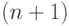 -разрядными, но это не страшно,
так как обработка лишнего разряда сводится к нескольким
сложениям.)
-разрядными, но это не страшно,
так как обработка лишнего разряда сводится к нескольким
сложениям.)Для размера схемы, таким образом, получается рекурсивная оценка

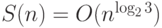 . В самом деле,
для умножения
. В самом деле,
для умножения  -разрядных чисел требуется дерево рекурсивных
вызовов глубины
-разрядных чисел требуется дерево рекурсивных
вызовов глубины 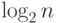 и степени ветвления
и степени ветвления  .
Заметим, что размер схемы в вершине пропорционален числу складываемых битов.
При переходе от одного уровня к следующему (более близкому к
корню) размер слагаемых растет вдвое, а число вершин уменьшается
втрое, поэтому общее число элементов на этом уровне уменьшается
в полтора раза. Таким образом, при движении по уровням от
листьев к корню получается убывающая геометрическая прогрессия
со знаменателем
.
Заметим, что размер схемы в вершине пропорционален числу складываемых битов.
При переходе от одного уровня к следующему (более близкому к
корню) размер слагаемых растет вдвое, а число вершин уменьшается
втрое, поэтому общее число элементов на этом уровне уменьшается
в полтора раза. Таким образом, при движении по уровням от
листьев к корню получается убывающая геометрическая прогрессия
со знаменателем  , сумма которой всего лишь втрое
превосходит ее первый член. Остается заметить, что число
листьев равно
, сумма которой всего лишь втрое
превосходит ее первый член. Остается заметить, что число
листьев равно  .
.Оценка глубины также очевидна: на каждом уровне мы имеем
схему сложения глубины  , а число уровней есть
, а число уровней есть  .
.
На этом мы завершаем знакомство со схемами из функциональных элементов, выполняющими арифметические операции. О них можно прочесть в главе 29 учебника Кормена, Лейзерсона и Ривеста [18] и в книге Ахо, Хопкрофта и Ульмана [1].
Рассмотрим теперь функцию "голосования"(majority).Она имеет
нечетное число аргументов, и значение ее равно  или
или  в зависимости от того, какое из двух значений
чаще встречается среди входов.
в зависимости от того, какое из двух значений
чаще встречается среди входов.
Теорема 14. Существует схема размера  и глубины
и глубины  ,
вычисляющая функцию голосования.
,
вычисляющая функцию голосования.
На самом деле можно даже вычислить общее число единиц среди
входов. Это делается рекурсивно: считаем отдельно для каждой
половины, потом складываем. Получается логарифмическое число
уровней. На верхнем уровне надо складывать числа размера  , на следующем— размера
, на следующем— размера 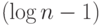 и так до самого
низа, где складываются однобитовые числа (то есть биты входа). Какой
средний размер складываемых чисел? Половина вершин в дереве
приходится на нижний уровень (числа длины
и так до самого
низа, где складываются однобитовые числа (то есть биты входа). Какой
средний размер складываемых чисел? Половина вершин в дереве
приходится на нижний уровень (числа длины  ), четверть — на
следующий (числа длины
), четверть — на
следующий (числа длины  ) и т. д. Вспоминая, что ряд
) и т. д. Вспоминая, что ряд 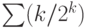 сходится, видим, что средний размер складываемых чисел
есть
сходится, видим, что средний размер складываемых чисел
есть 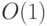 и общий размер схемы есть
и общий размер схемы есть  . А общая
глубина есть
. А общая
глубина есть  , так как на каждом из
, так как на каждом из  уровней стоит схема глубины
уровней стоит схема глубины 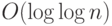 .
.
Заметим, что хотя функция голосования монотонна,
построенная схема ее вычисления содержит немонотонные элементы (поскольку операция
сложения не монотонна). Мы уже говорили, что всякую монотонную
функцию можно составить из конъюнкций и дизъюнкций. Для функции
голосования есть очевидный способ это сделать: написать
дизъюнкцию всех конъюнкций размера 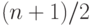 (напомним, что число
входов
(напомним, что число
входов  предполагается нечетным). Однако при этом получится
схема экспоненциального по
предполагается нечетным). Однако при этом получится
схема экспоненциального по  размера.
размера.
Теорема 15. Существует схема размера 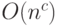 и глубины
и глубины  ,
составленная только из элементов И и ИЛИ (с двумя входами), вычисляющая функцию голосования.
,
составленная только из элементов И и ИЛИ (с двумя входами), вычисляющая функцию голосования.
Для начала заметим, что ограничение на размер
является следствием ограничения на глубину, так как элементы И и
ИЛИ имеют только два входа и число элементов в схеме глубины  есть
есть 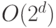 .
.
Схема будет строиться из элементов большинства с тремя входами.
(Каждый из них можно собрать из конъюнкций и дизъюнкций по
формуле 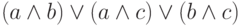 .)
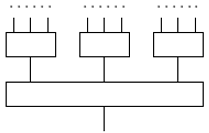
Выход схемы будет большинством из трех значений,
каждое из которых есть большинство из трех значений и т. д.
(рис. 2.3).
.)
Выход схемы будет большинством из трех значений,
каждое из которых есть большинство из трех значений и т. д.
(рис. 2.3).
Продолжая эту конструкцию на  уровнях, мы получим схему с
уровнях, мы получим схему с 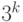 входами. (Отметим, что эта схема не будет вычислять
большинство среди своих входов — по той же причине, по которой
результат непрямого голосования может отличаться от мнения
большинства.) Но мы сделаем вот какую странную вещь: возьмем
входами. (Отметим, что эта схема не будет вычислять
большинство среди своих входов — по той же причине, по которой
результат непрямого голосования может отличаться от мнения
большинства.) Но мы сделаем вот какую странную вещь: возьмем  равным
равным  при достаточно большом коэффициенте
пропорциональности
при достаточно большом коэффициенте
пропорциональности  (при этом число входов такой схемы будет
полиномиально зависеть от
(при этом число входов такой схемы будет
полиномиально зависеть от  ) и напишем на входах случайно
выбранные переменные из данного нам набора
) и напишем на входах случайно
выбранные переменные из данного нам набора  .
(Переменные, записываемые на разных входах, выбираются
независимо.) Оказывается, что с ненулевой вероятностью эта схема
будет вычислять функцию большинства среди
.
(Переменные, записываемые на разных входах, выбираются
независимо.) Оказывается, что с ненулевой вероятностью эта схема
будет вычислять функцию большинства среди  ,
если константа
,
если константа  достаточно велика. Следовательно, искомая схема существует.
достаточно велика. Следовательно, искомая схема существует.
Обратите внимание: нам удастся доказать существование интересующей нас схемы, не предъявив ее явно. (Такое использование вероятностных методов в комбинаторных рассуждениях часто бывает полезно.)
Итак, почему же схема с положительной вероятностью вычисляет
функцию большинства? Это доказывается так: рассмотрим какой-то
один набор значений на входах и
докажем, что на этом конкретном наборе случайная схема
выдает правильный ответ с вероятностью, очень близкой к единице
(равной 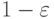 при очень малом
при очень малом  ).
).
Если число  настолько мало, что остается меньшим
единицы даже после умножения на число возможных входов (
настолько мало, что остается меньшим
единицы даже после умножения на число возможных входов ( 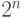 ),
то получаем требуемое (каждое из
),
то получаем требуемое (каждое из 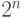 событий имеет вероятность
не меньше
событий имеет вероятность
не меньше 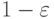 , значит их пересечение имеет
вероятность не меньше
, значит их пересечение имеет
вероятность не меньше 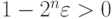 ).
).
Итак, осталось оценить вероятность того, что случайная схема
даст правильный ответ на данном входе. Пусть доля единиц среди
всех входов равна  . Тогда на каждый входной провод схемы
подается единица с вероятностью
. Тогда на каждый входной провод схемы
подается единица с вероятностью  и нуль с вероятностью
и нуль с вероятностью 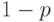 (выбор случайной переменной дает единицу с вероятностью
(выбор случайной переменной дает единицу с вероятностью  ),
причем сигналы на всех входах независимы.
),
причем сигналы на всех входах независимы.
Если на трех входах элемента  -большинства сигналы независимы,
и вероятность появления единицы на каждом входе есть
-большинства сигналы независимы,
и вероятность появления единицы на каждом входе есть  , то
вероятность появления единицы на выходе есть
, то
вероятность появления единицы на выходе есть 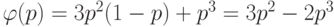 . На следующих уровнях
вероятность появления единицы будет равна
. На следующих уровнях
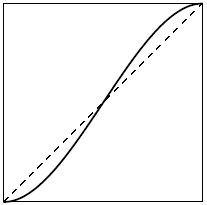
вероятность появления единицы будет равна 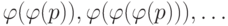 График
функции
График
функции 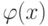 на отрезке
на отрезке ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) (рис. 2.4) показывает, что
при итерациях функции
(рис. 2.4) показывает, что
при итерациях функции  дисбаланс (отклонение от середины) нарастает и
последовательность стремится к краю отрезка. Надо только оценить число шагов.
дисбаланс (отклонение от середины) нарастает и
последовательность стремится к краю отрезка. Надо только оценить число шагов.
Если вначале единицы составляют большинство из  аргументов
(напомним,
аргументов
(напомним,  нечетно), то их как минимум
нечетно), то их как минимум 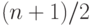 ,
так что
,
так что 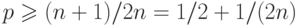 . Таким образом, начальный
дисбаланс составляет как минимум
. Таким образом, начальный
дисбаланс составляет как минимум 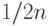 . А в конце нам нужно
приблизиться к краю отрезка на расстояние
. А в конце нам нужно
приблизиться к краю отрезка на расстояние 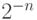 .
.
Итак, нам осталось доказать такую лемму (относящуюся скорее к математическому анализу):