|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Эконометрические методы управления качеством и сертификации продукции
Статистический контроль по двум альтернативным признакам и метод проверки их независимости по совокупности малых выборок
В настоящем пункте рассмотрим статистический приемочный контроль по двум альтернативным признакам одновременно. Обсуждается соотношение входного уровня дефектности изделия в целом с входными уровнями дефектности отдельных контролируемых параметров. На основе результатов статистики объектов нечисловой природы ( "Статистика нечисловых данных" ) рассмотрен метод проверки независимости двух альтернативных признаков. Метод нацелен на применение прежде всего в задачах статистического контроля качества продукции. При этом проверка независимости проводится по совокупности малых выборок, т.е. в так называемой асимптотике А.Н.Колмогорова, когда число неизвестных параметров распределения не является постоянным, а растет пропорционально объему данных.
При статистическом контроле качества продукции, в частности, при сертификации, чаще всего используют контроль по альтернативным признакам. При этом устанавливается, соответствует ли контролируемый параметр единицы продукции (изделия, детали) заданным в нормативно-технической документации требованиям или не соответствует. Если соответствует - единица продукции признается годной. Примем для определенности, что в этом случае результат контроля кодируется символом 0. Если же не соответствует - единица продукции признается дефектной, а результат контроля кодируется символом 1.
Таким образом, в рассматриваемой нами математической модели контроля альтернативный признак - это функция 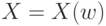 , определенная на множестве единиц продукции
, определенная на множестве единиц продукции 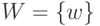 и принимающая два значения 0 и 1, причем
и принимающая два значения 0 и 1, причем 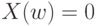 означает, что единица продукции
означает, что единица продукции  является годной, а
является годной, а 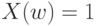 - что она является дефектной.
- что она является дефектной.
Методы статистического контроля, в частности, включенные в государственные стандарты и иную нормативно-техническую документацию (НТД), как правило, используют контроль по одному признаку. В НТД указывают правила выбора планов контроля и расчета различных их характеристик, приводят графики оперативных характеристик и т.п.
Однако на производстве контроль нередко проводится по нескольким альтернативным признакам. Возникает проблема выбора плана контроля и расчета его характеристик. В настоящее время для решения этой проблемы нет достаточно обоснованных и общепринятых рекомендаций.
Рассмотрим сначала контроль по двум альтернативным признакам  и
и 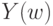 . В вероятностной модели
. В вероятностной модели  и
и 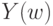 - случайные величины, принимающие два значения - 0 и 1. Пусть, пользуясь стандартной терминологией,
- случайные величины, принимающие два значения - 0 и 1. Пусть, пользуясь стандартной терминологией,
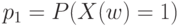
- входной уровень дефектности для первого признака, а
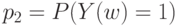
- для второго. Вероятности результатов контроля по двум признакам одновременно описываются четырьмя числами:
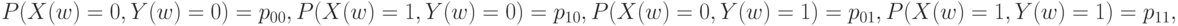
при этом справедливы соотношения:

С прикладной точки зрения наиболее интересна вероятность 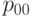 того, что единица продукции является годной (по всем параметрам), и вероятность ее дефектности
того, что единица продукции является годной (по всем параметрам), и вероятность ее дефектности 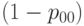 , т.е. входной уровень дефектности для изделия в целом.
, т.е. входной уровень дефектности для изделия в целом.
В табл.13.1 сведены вместе введенные выше вероятности.
| X=0 | X=1 | Всего | |
|---|---|---|---|
| Y=0 |  |
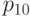 |
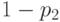 |
| Y=1 | 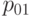 |
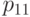 |
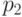 |
| Всего | 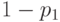 |
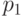 |
Есть три важных частных случая - поглощения, несовместности и независимости дефектов, другими словами, поглощения, несовместности и независимости событий 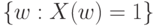 и
и 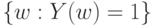 . В случае поглощения одно из этих событий содержит другое, а потому
. В случае поглощения одно из этих событий содержит другое, а потому
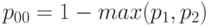
В случае несовместности

В случае независимости
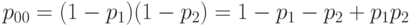
Очевидно, что вероятность годности изделия всегда заключена между значениями, соответствующими случаям поглощения и несовместности. Кроме того, известно, что при большом числе признаков и малой вероятности дефектности по каждому из них случаи поглощения и независимости дают (в асимптотике) крайние значения для вероятности годности изделия, т.е. формулы, соответствующие независимости и несовместности, асимптотически совпадают.
Рассмотрим несколько примеров. Пусть некоторая продукция, скажем, гвозди, контролируются по двум альтернативным признакам, для определенности, по весу и длине. Пусть результаты контроля 1000 единиц продукции представлены в табл.13.2.
| Х=0 | Х=1 | Всего | |
|---|---|---|---|
| У=0 | 952 | 0 | 952 |
| У=1 | 0 | 48 | 48 |
| Всего | 952 | 48 | 1000 |
Судя по данным табл.13.2, дефекты всегда встречаются парами - если есть один, то есть и другой. Входной уровень дефектности как по каждому показателю, так и по обоим вместе - один и тот же, а именно, 0,048. Получив по результатам статистического наблюдения данные типа приведенных в табл.13.2, целесообразно перейти к контролю только одного показателя, а не двух. Каково именно? Видимо, того, контроль которого дешевле. Однако совсем иная ситуация в случае несовместности дефектов (табл.).
| Х=0 | Х=1 | Всего | |
|---|---|---|---|
| У=0 | 904 | 48 | 952 |
| У=1 | 48 | 0 | 48 |
| Всего | 952 | 48 | 1000 |
Судя по данным табл., дефекты всегда встречаются поодиночке - если есть один, то другого нет. В результате входной уровень дефектности по каждому признаку по-прежнему равен 0,048, в то время как доля дефектных изделий (т.е. имеющих хотя бы один дефект) вдвое выше, т.е. входной уровень дефектности для изделия в целом равен 0,096.
Случай независимости результатов контроля по двум независимым признакам (табл.4) лежит между крайними случаями поглощения и несовместности. Независимость альтернативных признаков обосновывается путем статистической проверки с помощью описанного ниже критерия 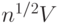 , значение которого для данных табл.13.4 равно 1,866.
, значение которого для данных табл.13.4 равно 1,866.
| Х=0 | Х=1 | Всего | |
|---|---|---|---|
| У=0 | 909 | 43 | 952 |
| У=1 | 43 | 5 | 48 |
| Всего | 952 | 48 | 1000 |
Согласно данным табл.13.4, входной уровень дефектности для каждого из двух альтернативных признаков по-прежнему равен 0,048, в то время как для изделий в целом он равен 0,091, т.е. на 5,5% меньше, чем в случае несовместности, и на 47% больше, чем в случае поглощения.
Проблема состоит в том, что таблицы и стандарты по статистическому приемочному контролю относятся обычно к случаю одного контролируемого параметра. А как быть, если контролируемых параметров несколько? Приведенные выше примеры показывают, что входной уровень дефектности изделия в целом не определяется однозначно по входным уровням дефектности отдельных его параметров.
Как должны соотноситься характеристики планов контроля по отдельным признакам с характеристиками плана контроля по двум (или многим) признакам одновременно? Рассмотрим распространенную рекомендацию - складывать уровни дефектности, т.е. считать, что уровень дефектности изделия в целом равен сумме уровней дефектности по отдельным его параметрам. Она, очевидно, опирается на гипотезу несовместности дефектов, а потому во многих случаях преувеличивает дефектность, а потому ведет к использованию излишне жестких планов контроля, что экономически невыгодно.
Зная специфику применяемых технологических процессов, в ряде конкретных случаев можно предположить, что дефекты по различным признакам возникают независимо друг от друга. Это предположение необходимо обосновывать по статистическим данным. Если же оно обосновано, следует рассчитывать входной уровень дефектности по формуле
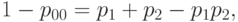
соответствующей независимости признаков.
Итак, необходимо уметь проверять по статистическим данным гипотезу независимости двух альтернативных признаков. Речь идет о статистической проверке нулевой гипотезы
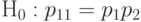 |
( 22) |
(что эквивалентно проверке равенства 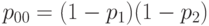 ). Нетрудно проверить, что гипотеза о справедливости равенства (22) эквивалентна гипотезе
). Нетрудно проверить, что гипотеза о справедливости равенства (22) эквивалентна гипотезе
 |
( 23) |
В простейшем случае предполагается, что проведено  независимых испытаний (
независимых испытаний ( 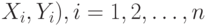 , в каждом из которых проконтролированы два альтернативных признака, а вероятности результатов контроля не меняются от испытания к испытанию. Общий вид статистических данных приведен в табл.13.5.
, в каждом из которых проконтролированы два альтернативных признака, а вероятности результатов контроля не меняются от испытания к испытанию. Общий вид статистических данных приведен в табл.13.5.
| Х=0 | Х=1 | Всего | |
|---|---|---|---|
| У=0 | a | b | a+b |
| У=1 |  |
 |
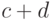 |
| Всего | 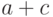 |
 |
 |
В табл.13.5 величина  - число испытаний, в которых
- число испытаний, в которых 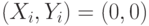 , величина
, величина  - число испытаний, в которых
- число испытаний, в которых 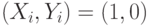 , и т.д.
, и т.д.
Случайный вектор 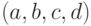 имеет мультиномиальное распределение с числом испытаний
имеет мультиномиальное распределение с числом испытаний  и вектором вероятностей исходов
и вектором вероятностей исходов 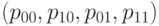 . Состоятельными оценками этих вероятностей являются дроби
. Состоятельными оценками этих вероятностей являются дроби 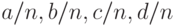 соответственно. Следовательно, критерий проверки гипотезы (23) может быть основан на статистике
соответственно. Следовательно, критерий проверки гипотезы (23) может быть основан на статистике
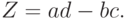 |
( 24) |
Как вытекает из известной формулы для ковариаций мультиномиального вектора (см., например, формулу (6.3.5) в учебнике С.Уилкса [14] на с. 153),
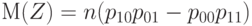 |
( 25) |
что равно 0 при справедливости гипотезы независимости (23).
Связь между переменными  и
и  обычно измеряется коэффициентом, отличающимся от
обычно измеряется коэффициентом, отличающимся от  нормирующим множителем:
нормирующим множителем:
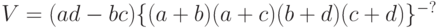 |
( 26) |
(см. классическую монографию М. Дж. Кендалла и А. Стьюарта [15, с.723], на которую уже были ссылки, в частности, в
"Многомерный статистический анализ"
). При справедливости гипотезы 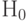 и больших
и больших  случайная величина
случайная величина  имеет хи-квадрат распределение с одной степенью свободы, а
имеет хи-квадрат распределение с одной степенью свободы, а 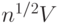 имеет стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1 (см. [15, с.736]).
имеет стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1 (см. [15, с.736]).
Рассмотрим еще один пример. Пусть проведено 100 испытаний, результаты которых описаны в табл.6. Тогда
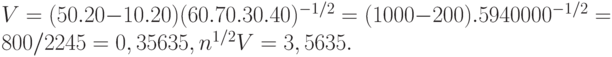
| Х=0 | Х=1 | Всего | |
|---|---|---|---|
| У=0 | 50 | 10 | 60 |
| У=1 | 20 | 20 | 40 |
| Всего | 70 | 30 | 100 |
Поскольку полученное значение 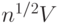 превышает критическое значение при любом применяемом в статистике уровне значимости, то гипотезу о независимости признаков необходимо отклонить.
превышает критическое значение при любом применяемом в статистике уровне значимости, то гипотезу о независимости признаков необходимо отклонить.
К сожалению, приведенный простой метод годится не всегда. При статистическом анализе реальных данных возникают проблемы, связанные с отсутствием достаточно больших однородных выборок, т.е. выборок, в которых постоянны параметры вероятностных распределений. Реально единицы продукции представляются на контроль партиями, из каждой партии контролируются лишь несколько изделий, т.е. малая выборка. При этом от партии к партии меняются параметры 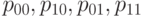 , описывающие уровень дефектности. Поэтому необходимы статистические методы, позволяющие проверять гипотезу независимости признаков по совокупности малых выборок. Построим один из возможных методов.
, описывающие уровень дефектности. Поэтому необходимы статистические методы, позволяющие проверять гипотезу независимости признаков по совокупности малых выборок. Построим один из возможных методов.
Рассмотрим вероятностную модель совокупности  малых выборок объемов
малых выборок объемов 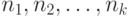 соответственно. Пусть
соответственно. Пусть  -я выборка
-я выборка 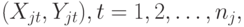 имеет распределение, задаваемое вектором параметров
имеет распределение, задаваемое вектором параметров 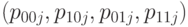 в соответствии с ранее введенными обозначениями,
в соответствии с ранее введенными обозначениями, 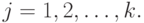 Будем проверять гипотезу
Будем проверять гипотезу
 |
( 27) |
или в эквивалентной формулировке
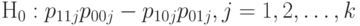 |
( 28) |
Основная идея состоит в нахождении асимптотического распределения статистики типа 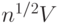 при росте числа
при росте числа  малых выборок, а именно, статистики
малых выборок, а именно, статистики
 |
( 29) |
где 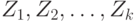 - статистики, рассчитанные по формуле (24) для каждой из
- статистики, рассчитанные по формуле (24) для каждой из  выборок, т.е.
выборок, т.е. 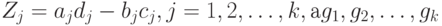 - некоторые весовые коэффициенты, которые, в частности, могут совпадать. Поскольку
- некоторые весовые коэффициенты, которые, в частности, могут совпадать. Поскольку
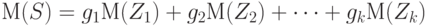 |
( 30) |
то при справедливости гипотезы независимости (27) - (28) имеем 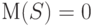 согласно соотношению (25). Поскольку слагаемые в сумме (29) независимы, то при росте
согласно соотношению (25). Поскольку слагаемые в сумме (29) независимы, то при росте  случайная величина
случайная величина  в силу Центральной Предельной Теоремы является асимптотически нормальной. Дисперсия этой величины равна сумме дисперсий слагаемых:
в силу Центральной Предельной Теоремы является асимптотически нормальной. Дисперсия этой величины равна сумме дисперсий слагаемых:
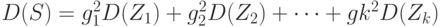 |
( 31) |
Для оценивания дисперсии  необходимо использовать несмещенные оценки дисперсий в каждой из
необходимо использовать несмещенные оценки дисперсий в каждой из  выборок (и в этом одна из основных "изюминок" разбираемого метода). Предположим, что построены статистики Tj такие, что
выборок (и в этом одна из основных "изюминок" разбираемого метода). Предположим, что построены статистики Tj такие, что
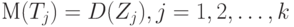 |
( 32) |
Тогда при некоторых математических "условиях регулярности", на которых нет необходимости здесь останавливаться, несмещенная оценка дисперсии статистики  , имеющая согласно формулам (31) и (32) вид
, имеющая согласно формулам (31) и (32) вид
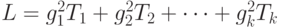 |
( 33) |
в силу закона больших чисел такова, что дробь 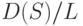 приближается к 1 при росте числа выборок (сходимость по вероятности). Отсюда следует, что распределение случайной величины
приближается к 1 при росте числа выборок (сходимость по вероятности). Отсюда следует, что распределение случайной величины  приближается при росте числа выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Следовательно, критерий проверки гипотезы (27) - (28) независимости признаков, состоящий в том, что при
приближается при росте числа выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Следовательно, критерий проверки гипотезы (27) - (28) независимости признаков, состоящий в том, что при 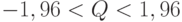 гипотеза принимается, а при Q , выходящих за пределы интервала
гипотеза принимается, а при Q , выходящих за пределы интервала 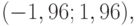 гипотеза отклоняется, имеет уровень значимости, приближающийся к 0,05 при росте числа выборок. Мощность этого критерия зависит от величины
гипотеза отклоняется, имеет уровень значимости, приближающийся к 0,05 при росте числа выборок. Мощность этого критерия зависит от величины 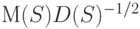 при альтернативе.
при альтернативе.
Для реализации намеченного плана осталось научиться несмещенно оценивать  . К сожалению, в литературе по несмещенному оцениванию не рассматривают случай мультиномиального распределения, поэтому кратко опишем процедуру построения несмещенной оценки
. К сожалению, в литературе по несмещенному оцениванию не рассматривают случай мультиномиального распределения, поэтому кратко опишем процедуру построения несмещенной оценки  . Поскольку согласно формулам (24) и (25)
. Поскольку согласно формулам (24) и (25)
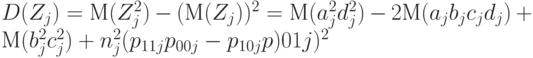 |
( 34) |
то для вычисления  достаточно найти входящие в правую часть формулы (34) начальные смешанные моменты мультиномиального распределения (четвертого порядка). Теоретически это просто - известен вид характеристической функции мультиномиального распределения, а начальные смешанные моменты равны значениям ее соответствующих производных в 0, деленным на нужную степень мнимой единицы. Например, с помощью описанной процедуры после некоторых вычислений получаем, что (для упрощения записи здесь и далее опустим индекс
достаточно найти входящие в правую часть формулы (34) начальные смешанные моменты мультиномиального распределения (четвертого порядка). Теоретически это просто - известен вид характеристической функции мультиномиального распределения, а начальные смешанные моменты равны значениям ее соответствующих производных в 0, деленным на нужную степень мнимой единицы. Например, с помощью описанной процедуры после некоторых вычислений получаем, что (для упрощения записи здесь и далее опустим индекс  )
)
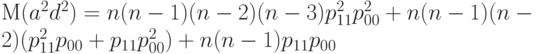 |
( 35) |
Формула (35) показывает, что начальные смешанные моменты мультиномиального распределения являются многочленами от параметров 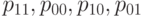 этого распределения, однако конкретный вид этих многочленов достаточно громоздок, поэтому не будем их здесь выписывать, ограничившись формулой (35) в качестве образца.
этого распределения, однако конкретный вид этих многочленов достаточно громоздок, поэтому не будем их здесь выписывать, ограничившись формулой (35) в качестве образца.
Как вытекает из формул (34) и (35), для построения несмещенной оценки  достаточно научиться несмещенно оценивать произведения типа
достаточно научиться несмещенно оценивать произведения типа 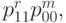 где целые неотрицательные числа
где целые неотрицательные числа 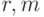 не превосходят 2. Эта задача решается, начиная с меньших степеней. Известно, что для ковариации мультиномиального вектора
не превосходят 2. Эта задача решается, начиная с меньших степеней. Известно, что для ковариации мультиномиального вектора
 |
( 36) |
(см., например, формулу (6.3.5) в монографии [14, с.153]), а потому несмещенной оценкой для  является
является 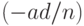 . Далее, поскольку справедлива аналогичная (35) формула
. Далее, поскольку справедлива аналогичная (35) формула
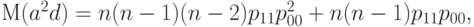 |
( 37) |
то с помощью формулы (36) преобразуем формулу (37) к виду
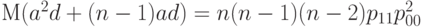 |
( 38) |
т.е. несмещенной оценкой  является
является 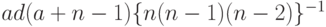 .
.
Следующий шаг - аналогичным образом с помощью формул (36) и (38) получаем несмещенную оценку для 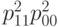 , а затем и для
, а затем и для  Промежуточные формулы опущены из-за громоздкости. Окончательный результат таков:
Промежуточные формулы опущены из-за громоздкости. Окончательный результат таков:
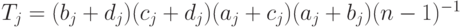 |
( 39) |
Как легко видеть,

т.е. в случае одной выборки предлагаемый метод совпадает с классическим.
Общая идея рассматриваемого метода проверки гипотез по совокупности малых выборок состоит в том, что подбирается статистика, математическое ожидание которой для каждой малой выборки равно 0 при справедливости проверяемой гипотезы. Затем для каждой выборки строится несмещенная оценка дисперсии этой статистики. Итоговая статистика критерия для проверки гипотезы - это сумма рассматриваемых статистик для всех малых выборок, деленная на квадратный корень из суммы всех несмещенных оценок дисперсий рассматриваемых статистик. При справедливости нулевой гипотезы эта итоговая статистика имеет в асимптотике стандартное нормальное распределение (при выполнении некоторых математических "условий регулярности", которые обычно выполняются при анализе реальных статистических данных).
Впервые такой способ проверки гипотез по совокупности малых выборок был предложен в монографии [16, раздел 4.5]. Нестандартность постановки состоит в том, что число неизвестных параметров растет пропорционально объему данных, т.е. имеет место т.н. "асимптотика Колмогорова", или асимптотика растущей размерности. Дальнейшее развитие применительно к данных типа "да"-"нет" (или "годен" - "дефектен") шло в рамках теории люсианов как части статистики объектов нечисловой природы (см. "Статистика нечисловых данных" ).
