|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Эконометрические методы управления качеством и сертификации продукции
Асимптотическая теория одноступенчатых планов статистического контроля
Пусть  - число дефектных единиц продукции в выборке объема
- число дефектных единиц продукции в выборке объема  . Как уже отмечалось, распределение
. Как уже отмечалось, распределение  является биномиальным и имеет вид
является биномиальным и имеет вид
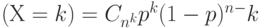
где  - число сочетаний из
- число сочетаний из  элементов по
элементов по  ,
,  - входной уровень дефектности.
- входной уровень дефектности.
Пусть используется одноступенчатый план контроля 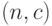 . Тогда оперативная характеристика этого плана имеет вид
. Тогда оперативная характеристика этого плана имеет вид
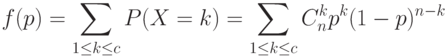
Пусть 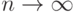 Тогда по Закону Больших Чисел теории вероятностей (по теореме Бернулли)
Тогда по Закону Больших Чисел теории вероятностей (по теореме Бернулли)

(сходимость по вероятности). Значит, если 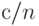 окажется заметно больще входного уровня дефектности
окажется заметно больще входного уровня дефектности 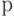 , то партии будут почти всегда приниматься, а если
, то партии будут почти всегда приниматься, а если 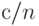 окажется заметно меньше входного уровня дефектности
окажется заметно меньше входного уровня дефектности 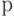 , то партии будут почти всегда отклоняться. Ситуация будет нетривиальной только там, где величины
, то партии будут почти всегда отклоняться. Ситуация будет нетривиальной только там, где величины 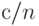 и
и 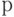 близки друг к другу.
близки друг к другу.
Хотя оперативная характеристика приближается с помощью сумм биномиальных вероятностей, целесообразно найти для нее приближение с помощью теоремы Муавра-Лапласа. Имеем цепочку тождественных преобразований:

Однако справа строит именно то выражение, которое участвует в теореме Муавра-Лапласа. Воспользовавшись равномерной сходимостью в этой теореме, можно записать, что
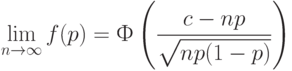
где  - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
Последняя формула позволяет без труда написать асимптотические выражения для приемочного и браковочного уровней дефектности. Действительно, согласно определениям этих понятий
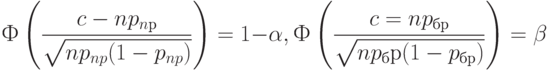 |
( 10) |
откуда с помощью элементарных преобразований получаем, что
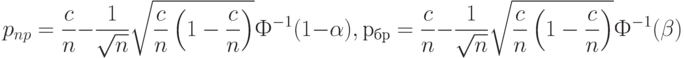 |
( 11) |
Так как величины 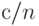 и
и 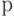 близки друг к другу, то при переходе от формулы (10) к формуле (11) в подкоренных выражениях приемочный и браковочный уровни дефектности заменены на
близки друг к другу, то при переходе от формулы (10) к формуле (11) в подкоренных выражениях приемочный и браковочный уровни дефектности заменены на 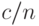 (с точностью до бесконечно малых более высокого порядка).
(с точностью до бесконечно малых более высокого порядка).
Поскольку при практическом применении статистического приемочного контроля, как уже отмечалось, принимают 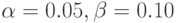 , то в предыдущие формулы следует подставить
, то в предыдущие формулы следует подставить 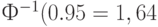 и
и 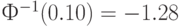 Итак, итоговые формулы для приемочного и браковочного уровней дефектности имеют вид
Итак, итоговые формулы для приемочного и браковочного уровней дефектности имеют вид
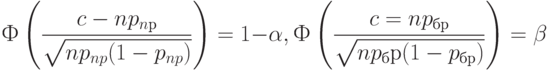
Перейдем к задаче синтеза. Пусть заданы приемочный и браковочный уровни дефектности. Требуется построить одноступенчатый план, имеющий эти характеристики. Из формул (10) следует, в частности, что
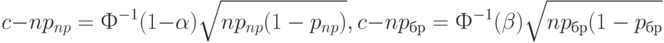 |
( 12) |
Вычитая из первого уравнения второе, получаем, что

Следовательно, оценка необходимого объема выборки имеет вид
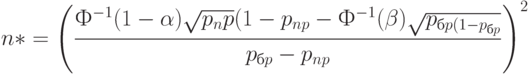
Для стандартных значений рисков 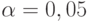 ,
, 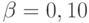 имеем:
имеем:
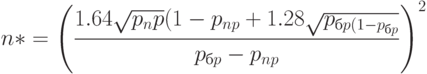 |
( 13) |
С помощью уравнений (12) нетрудно найти оценку 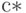 приемочного числа, заменив неизвестный объем выборки на его оценку
приемочного числа, заменив неизвестный объем выборки на его оценку 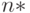 . Будем использовать оценку
. Будем использовать оценку
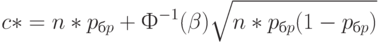
Для стандартного значения 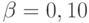 имеем
имеем
 |
( 14) |
Итак, по формуле (13) можно рассчитать оценку объема выборки, затем по формуле (14) найти оценку приемочного числа. Необходимо отметить, что результаты расчетов по рассматриваемым асимптотическим формулам отнюдь не всегда дают целые числа, поэтому необходима корректировка полученных результатов.
Полученные формулы позволяют решить сформулированную выше задачу - по заданным приемочному и браковочному уровням дефектности подобрать такой одноступенчатый план контроля, что его оперативная характеристика 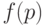 удовлетворяет неравенствам
удовлетворяет неравенствам
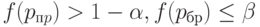
Поэтому при практической работе корректировка асимптотических результатов должна быть направлена на выполнение указанных неравенств.
Пример. Пусть 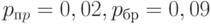 . Тогда по формуле (13) оценка объема выборки равна
. Тогда по формуле (13) оценка объема выборки равна
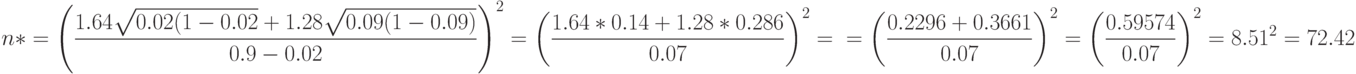
Полученное число не является натуральным, поэтому вполне естественно откорректировать объем выборки до ближайшего целого, т.е. до 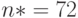 .
.
Оценку приемочного числа находим по формуле (14):
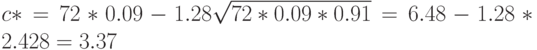
Полученное число не является целым, поэтому в качестве приемочного числа надо взять ближайшее целое, т.е. до 3.
Если объем выборки округлить до 73, то аналогично получим
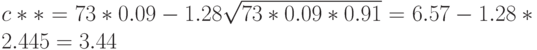
При округлении снова получаем 3.
С помощью первого из уравнений (12) можно построить оценку 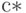 на основе приемочного уровнея дефектности:
на основе приемочного уровнея дефектности:
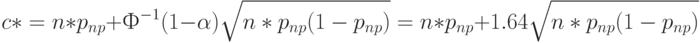
Подставив конкретные значения, получим практически ту же оценку, что и раньше:
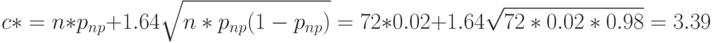
Итак, в результате асимптотических расчетов найден одноступенчатый план (72, 3).
