|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методика сравнительного анализа родственных эконометрических моделей
П3-5. Методы согласования ранжировок
- Методы раздела 5 применяются в соответствии с п.2.6 для согласования ранжировок родственных моделей, полученных с помощью теоретических или эмпирических единичных показателей качества моделей, а также ранжировок, построенных на основе групповых показателей качества, в частности, показателей, рассмотренных в пп.3.2 - 3.6.
- При согласовании ранжировок исходят из двух или нескольких ранжировок, вообще говоря, со связями (нестрогих линейных порядков). В каждой ранжировке модели располагаются в порядке понижения качества, причем некоторые модели могут признаваться эквивалентными (по рассматриваемому показателю качества). Ранжировки моделей могут быть получены как при их объективном сравнении по различным показателям качества, так и от экспертов, сравнивающих модели по тому или иному показателю или их набору.
- На первом этапе согласования ранжировок выделяются противоречивые пары моделей. Пара моделей А и В признается противоречивой, если в одной из рассматриваемых ранжировок модель А строго лучше модели В, а в какой-то другой модель В строго лучше модели А. Тем самым определяется симметричное бинарное отношение (квазитолерантность) на множестве моделей.
- В соответствии с правилами теории бинарных отношений проводится транзитивное замыкание квазитолерантности, построенной в соответствии с п. 5.3. Устанавливается порядок между классами эквивалентности, соответствующий порядкам во всех исходных ранжировках. Полученная ранжировка называется согласующей для множества исходных ранжировок. При сравнении согласующей ранжировки с любой из исходных не существует ни одной противоречивой пары (это вытекает из теорем, приведенных в пункте П3-8 ниже).
- При необходимости упорядочения по качеству моделей, входящих в один класс согласующей ранжировки (т.е. эквивалентных в соответствии с ней), привлекается дополнительная информация. Эта информация может опираться на дополнительные показатели качества, на результаты дополнительных исследований, как экспериментальных, так и теоретических, в частности, проведенных методами статистики объектов нечисловой природы (см. "Статистика нечисловых данных" ).
П3-6. Методы проверки согласованности, кластеризации и усреднения ранжировок
- При необходимости упорядочения по качеству моделей, входящих в один класс согласующей ранжировки (п.5.5), применяют методы проверки (статистической) согласованности, при необходимости - кластерного анализа, а затем - усреднения ранжировок, разработанные в статистике объектов нечисловой природы.
-
Методы, указанные в п.6.1, предполагают использование того или иного расстояния (меры различия) в пространстве ранжировок (со связями). В соответствии с методологией настоящей методики используется расстояние Кемени-Снелла, связанное с коэффициентом ранговой корреляции Кендалла, при проверке (статистической) согласованности и - при необходимости - проведении кластерного анализа. При усреднении ранжировок используется мера различия, основанная на коэффициенте ранговой корреляции Спирмена. Допускается использование иных расстояний и мер близости (различия) в том числе:
- расстояния, основанного на понятии ближайшего соседа;
- иных расстояний и мер близости, разработанных в статистике объектов нечисловой природы.
- При использовании одновременно нескольких расстояний (мер различия или близости) в пространстве ранжировок (со связями) в соответствии с методологией настоящей методики необходимо использовать выводы, устойчивые относительно выбора того или иного расстояния (меры различия) в пространстве ранжировок (со связями).
- В соответствии с методологией настоящей методики сначала проверяется согласованность набора ранжировок с помощью коэффициента ранговой конкордации Кендалла и Бебингтона Смита (при небольшом числе связей) или теории люсианов (если ранжировки построены на основе парных сравнений моделей), а также согласованность оценивается экспертно.
- В случае недостаточной согласованности набора ранжировок проводится их разбиение на группы схожих между собой тем или иным методом кластерного анализа. Результат разбиения должен быть достаточно устойчив относительно выбора метода кластер-анализа. Деление показателей качества на группы, по которым модели оцениваются схожим образом, или экспертов на группы с близкими мнениями используется неформально при дальнейшем сравнении родственных математических моделей.
- При положительном ответе на вопрос о согласованности ранжировок результирующая (итоговая) ранжировка находится как эмпирическое среднее (медиана Кемени) согласно статистике объектов нечисловой природы (с учетом сказанного в пп. 6.2, 6.3). При отрицательном ответе на вопрос о согласованности ранжировок результирующие (итоговые) ранжировки находятся отдельно для каждого кластера.
- Информация о расчетных формулах по методам раздела 6 и их теоретических основах приведены в пункте П3-9 ниже.
П3-7. Пример сравнения родственных эконометрических моделей на основе эмпирических единичных показателей качества
При решении задач экологического страхования необходимо проанализировать последствия возможных аварий на химических производствах. Другими словами, в экологическом страховании экономические проблемы переплетаются с проблемами химической безопасности биосферы. Поэтому нет ничего удивительного в том, что в качестве примера рассматриваются 8 родственных эконометрических (если угодно - математических) моделей стационарных процессов испарения жидкости с открытых поверхностей. Модели будем различать по фамилиям предложивших и изучавших их специалистов. Это модели Лебузера (в дальнейшем кратко Л), Мак-Кея (М-К), Гусева-Баранаева (Г-Б), Клячко (К), Стефана (Стеф), Братсерта (Б), Дикона (Д), Соломона (Сол). Имеются данные о 12 конкретных экспериментах. Для соответствующих 12 наборов входных переменных получены расчетные значения по упомянутым 8 моделям. В табл.1 приведены значения относительных погрешностей (в процентах и без учета знака) расчетных значений относительно реальных.
В последней строке табл.1 в соответствии с п.4.4 методики приведены суммы относительных отклонений результатов измерений от расчетных значений. Упорядочение (ранжировка) по сумме относительных погрешностей (отклонений) имеет вид:
 |
( 1) |
В табл.2 приведены ранги 8 моделей по точности приближения в отдельных экспериментальных точках (ранг 1 - самая точная модель, ранг 2 - вторая по точности,\dots, ранг 8 - самая далекая от истинного экспериментального значения модель). Они получены путем сравнения относительных погрешностей из табл.1.
| № эксп. | Д | Л | М-К | Б | Г-Б | Сол | Стеф | К |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 3 | 1 | 2 | 8 | 4 | 6 | 7 |
| 2 | 5 | 4 | 3 | 1 | 8 | 2 | 6 | 7 |
| 3 | 1 | 7 | 5 | 4 | 8 | 2 | 3 | 6 |
| 4 | 6 | 4 | 2,5 | 2,5 | 8 | 1 | 7 | 5 |
| 5 | 7 | 1 | 3 | 5 | 2 | 4 | 8 | 6 |
| 6 | 5 | 6 | 4 | 3 | 2 | 1 | 7 | 8 |
| 7 | 6 | 1 | 2 | 3 | 5 | 4 | 8 | 7 |
| 8 | 5 | 1 | 3 | 2 | 7 | 4 | 6 | 8 |
| 9 | 6 | 1 | 3 | 2 | 5 | 4 | 7 | 8 |
| 10 | 5 | 3 | 2 | 1 | 8 | 4 | 6 | 7 |
| 11 | 7 | 1 | 2 | 2 | 6 | 4 | 5 | 8 |
| 12 | 1 | 6 | 5 | 3 | 8 | 4 | 2 | 7 |
| Сумма | 59 | 38 | 36,5 | 30.5 | 75 | 38 | 71 | 84 |
| Итоговый ранг | 5 | 3,5 | 2 | 1 | 7 | 3.5 | 6 | 8 |
В соответствии с п.4.5 ранги складываются по всем экспериментальным точкам (суммы приведены в предпоследней строке табл.2) и модели ранжируются в порядке возрастания суммы рангов. Итоговый ранг приведен в последней строке табл.2. Ранжировка по суммам рангов (или, что то же, по средним арифметическим рангов) имеет вид:
 |
( 2) |
Поскольку модели 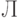 и
и  получили одинаковую сумму баллов, то по этому показателю они эквивалентны, а потому объединены в группу (кластер), т.е. ранжировка (2) имеет одну связь.
получили одинаковую сумму баллов, то по этому показателю они эквивалентны, а потому объединены в группу (кластер), т.е. ранжировка (2) имеет одну связь.
Сравнивая ранжировки (1) и (2), видим, что они весьма похожи. Они отличаются только по двум позициям:
- стоящие рядом в ранжировке (1) модели
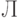 и
и  в ранжировке (2) объединены в один кластер;
в ранжировке (2) объединены в один кластер; - модели
 и
и 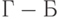 расположены в ранжировках (1) и (2) в противоположном порядке.
расположены в ранжировках (1) и (2) в противоположном порядке.
В соответствии с п.5.3. на первом этапе согласования ранжировок следует выделить противоречивые пары моделей. При сравнении ранжировок (1) и (2) только пара моделей  и
и 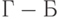 признается противоречивой. Следовательно, для ранжировок (1) и (2) согласующей является кластеризованная ранжировка
признается противоречивой. Следовательно, для ранжировок (1) и (2) согласующей является кластеризованная ранжировка
 |
( 3) |
в которой модели упорядочены от лучшей к худшей.
Рассмотрим теперь дополнительные методы ранжирования, предусмотренные п. 4.6 настоящей методики. Вариантом метода ранжировки по числу экспериментальных точек, в которых модель оказалась наилучшей (без учета знака отклонения), является метод разбиения рассматриваемой совокупности родственных моделей на два класса - тех, которые оказались наилучшими хотя бы для одной экспериментальной точки (т.е. оптимальных по Парето), и остальных, никогда не бывших наилучшими. В первое множество входят модели  , являющиеся оптимальными по Парето на рассматриваемом множестве экспериментальных точек, во второе - остальные модели, т.е.
, являющиеся оптимальными по Парето на рассматриваемом множестве экспериментальных точек, во второе - остальные модели, т.е. 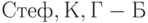 , и соответствующая ранжировка со связями имеет вид
, и соответствующая ранжировка со связями имеет вид
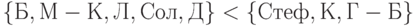 |
( 4) |
Ранжировка (4) не имеет противоречивых пар с ранжировкой (3), поэтому можно считать, что ранжировка (3) является согласующей для всех трех ранжировок (1), (2), (4).
Другой вариант, предусмотренный п.4.6, предполагается учет числа точек, в которых та или иная из рассматриваемой совокупности родственных моделей оказалась наилучшей (наиболее точной). Чем в большем числе точек модель оказалась точнее, тем выше она оценивается. Модель Л является наилучшей в 5 экспериментах (№№ 5, 7, 8, 9, 11), модель Б - в 2 экспериментах (№№ 2, 10), как и модели Д (эксперименты №№ 3, 12) и Сол (эксперименты №№ 4, 6), модель М-К - в одном (№ 1), остальные - ни разу. Ранжировка имеет вид:
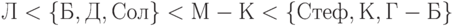 |
( 5) |
Сопоставим ранжировки (3) и (5). Имеем следующие четыре противоречивые пары: 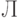 и
и 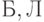 и
и  и
и  ,
,  и
и  . Значит, в один кластер с
. Значит, в один кластер с  надо включить
надо включить 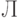 ,
,  и
и  , а раз модель
, а раз модель 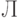 связана противоречием в
связана противоречием в 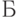 , то и
, то и  надо включить в этот кластер, состоящий в итоге из 5 моделей -
надо включить в этот кластер, состоящий в итоге из 5 моделей - 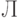 ,
,  . Итоговая ранжировка имеет вид:
. Итоговая ранжировка имеет вид:
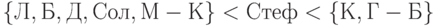 |
( 6) |
Она является согласующей для четырех ранжировок (1), (2), (4), (5). (Напомним, что кластер 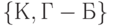 появился как следствие противоречия в упорядочении моделей
появился как следствие противоречия в упорядочении моделей  и
и 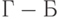 в ранжировках (1) и (2).)
в ранжировках (1) и (2).)
Выше приведены результаты формального анализа семейства 8 родственных моделей по 4 критериям. Общее заключение должно быть сделано экспертным путем.
В данной ситуации по мнению экспертов итогом сравнения моделей должна быть признана ранжировка (3), являющаяся согласующей для 3 из 4 критериев:

Ранжировка (6), согласующая для всех четырех критериев, объявляет эквивалентными 5 наиболее интересных моделей, поскольку оставшиеся 3 модели по результатам анализа экспериментальных данных можно вообще исключить из дальнейшего рассмотрения. Согласно п. 5.5 в случае необходимости упорядочения моделей, попавших в один кластер, привлекается дополнительная информация. В рассматриваемом случае дополнительная информация дает основания исключить один из четырех критериев.
В "Эконометрические методы проведения экспертных исследований и анализа оценок экспертов" 12 процедура согласования ранжировок использовалась при анализе мнений экспертов. Однако в настоящем приложении 3 речь идет не о мнениях экспертов, а о сравнении эконометрических моделей. Исходные данные - табл.1 - результаты измерений, а не субъективные оценки.
