Методика сравнительного анализа родственных эконометрических моделей

О согласовании классификаций. Пусть имеются две классификации и 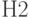, разбивающие множества объектов на кластеры 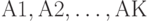и 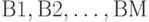соответственно. Рассмотрим новую классификацию , построенную на основе пересечений множеств 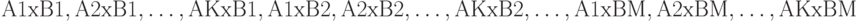(здесь - знак пересечения). Число кластеров в - не более 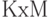, поскольку некоторые из выписанных пересечений могут оказаться пустыми. Классификация обладает тем свойством, что любые два элемента, входящие в один из ее кластеров, входят также в один кластер и в , и в 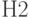. Если же два элемента входят в разные кластеры , то либо в , либо в 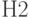, либо одновременно и в , и в 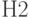они входят в разные кластеры. Поэтому можно сказать, что классификация согласует классификации и .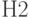

Для классификаций с неупорядоченными кластерами сказанное в предыдущем абзаце решает проблему согласования. Для классификаций, кластеры которых строго линейно (или совершенно) упорядочены [2, с.119-120], т.е. порожденных склейкой одинаковых значений некоторого агрегирующего показателя на множестве объектов (существование такого показателя вытекает из теоремы 4.2 в [2, с.121-122]), можно продвинуться дальше.

Описанная выше процедура согласования классификаций, полученных различными способами на основе двух ранжировок, является общей. Она может быть применена для согласования любых двух классификаций, использующих строго линейно упорядоченные кластеры.

Сначала необходимо построить "квазитолерантность расхождений ", включающую те и только те пары объектов, упорядоченность которых в двух классификациях различна. Затем строим "толерантность расхождений (ТР)", добавляя к все пары вида 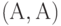. Затем строим 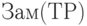, транзитивно замыкая 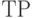по правилам теории бинарных отношений [2, с.27]. Корректность этой процедуры обеспечивает следующая теорема.

Теорема 2. Замыкание толерантности расхождений Зам(ТР) задает классификацию на упорядоченные кластеры. При этом все объекты одного кластера одновременно лучше (или одновременно хуже) всех объектов другого кластера одновременно по обоим используемым агрегированным показателям. Внутри же кластеров, состоящих более чем из одного элемента, имеются противоречия: для какого-то объекта есть другой из того же кластера такой, что упорядочение по одному агрегированному показателю противоречит упорядочению по другому агрегированному показателю.

Доказательство. Как показано при доказательстве теоремы 1, 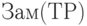является отношением эквивалентности, а потому задает некоторое разбиение множества объектов, т.е. классификацию.

Просматривая доказательство теоремы 1, нетрудно заметить, что в нем не используются какие-либо конкретные свойства взвешенной медианы или взвешенного среднего арифметического, а потому проведенные рассуждения верны для любых строгих совершенных (линейных) порядков. Это замечание и заканчивает доказательство теоремы 2.

Замечание. Расчет согласующей классификации как 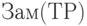не всегда дает приемлемые с практической точки зрения результаты. Пусть например, имеется 4 объекта, описываемые точками на плоскости 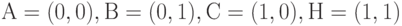, первое упорядочение - по первой координате, второе - по второй (каждое из упорядочений имеет два варианта соответственно тому, как интерпретировать равенство, т.е. использовать отношение "меньше" или "меньше или равно"). Нетрудно проверить, что 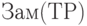дает вырожденную классификацию - состоит из одного кластера. Между тем другие способы построения результирующего упорядочения, например, по сумме координат, могут оказаться более практически приемлемы.

Практический интерес представляет также задача расширения классификации по упорядоченным классам, заданной на части естественного множества определения, на все это множество. Решений, как правило, имеется несколько, и возникают проблемы описания всех возможных расширений и выбора из них наиболее адекватного с точки зрения рассматриваемой прикладной области, например, токсикологии как части экологического страхования.

Об алгоритмах нахождения согласующей кластеризованной ранжировки. Пусть дана конечная совокупность ранжировок моделей (возможно, со связями). Требуется построить согласующую ранжировку, возможно, кластеризованную (т.е. со связями).

Шаг 1. Находим все пары моделей, упорядочение которых хотя бы в двух исходных ранжировках противоречиво (в одной ранжировке первая модель строго лучше второй, а в другой ранжировке - наоборот, вторая модель строго лучше первой).

Шаг 2. Рассмотрим граф, вершины которого - модели из рассматриваемого семейства родственных моделей. Две вершины соединены ребром тогда и только тогда, когда они выделены на шаге 1. Выделяем связные компоненты этого графа.

Шаг 3. Устанавливаем строгий порядок между связными компонентами графа, выделенными на шаге 2 (кластерами). Получаем искомую согласующую ранжировку.

Программная реализация описанной схемы может быть осуществлена различными способами.

П3-8. Теоретические основы методов проверки согласованности, кластеризации и усреднения ранжировок

Как указано в п.6.1 настоящей методики, при необходимости упорядочения по качеству моделей, входящих в один класс согласующей кластеризованной ранжировки, применяют методы проверки (статистической) согласованности, при необходимости - кластерного анализа, а затем - усреднения ранжировок, разработанные в статистике объектов нечисловой природы. Эти методы предполагают использование того или иного расстояния (меры различия) в пространстве ранжировок (со связями). В соответствии с методологией настоящей методики используется расстояние Кемени-Снелла (см. "Статистика нечисловых данных" , а также монографию [3]), связанное с коэффициентом ранговой корреляции Кендалла, при проверке (статистической) согласованности и - при необходимости - проведении кластерного анализа. При усреднения ранжировок часто используется мера различия, основанная на коэффициенте ранговой корреляции Спирмена (см. [4]). Допускается использование иных расстояний и мер близости (различия) в том числе:

• расстояния, основанного на понятии ближайшего соседа;
• иных расстояний и мер близости, разработанных в статистике объектов нечисловой природы (см. "Статистика нечисловых данных" и монографии [5] ).

При использовании одновременно нескольких расстояний (мер различия или близости) в пространстве ранжировок (со связями) в соответствии с методологией теории устойчивости ( "Проблемы устойчивости эконометрических процедур" ) необходимо использовать выводы, устойчивые относительно выбора того или иного расстояния (меры различия) в пространстве ранжировок (со связями).

Сначала проверяется согласованность набора ранжировок с помощью коэффициента ранговой конкордации Кендалла и Бебингтона Смита (при небольшом числе связей) согласно [4, табл. 6.10]. Если ранжировки построены на основе парных сравнений моделей, то используются методы теории люсианов (см., например, [7]; пример алгоритмов из теории люсианов описан выше в "Эконометрические методы управления качеством и сертификации продукции" ). Согласованность экспертов может также оцениваться с помощью другой группы экспертов.

В случае недостаточной согласованности набора ранжировок, т.е. отклонения гипотезы согласованности на уровне значимости 5 % или более низком, проводится их разбиение на группы схожих между собой тем или иным методом кластерного анализа (см. "Многомерный статистический анализ" ). Согласно методологии устойчивости (см. "Проблемы устойчивости эконометрических процедур" ) результат разбиения должен быть достаточно устойчив относительно выбора метода кластер-анализа. Рекомендуется одновременно использовать метод ближнего соседа и метод дальнего соседа, используя в дальнейшем устойчивые ядра кластеров, выделяющиеся при одновременном применении указанных двух методов.

Деление показателей качества на группы, по которым модели оцениваются схожим образом, или экспертов на группы с близкими мнениями используется участниками проекта и пользователями банка эконометрических моделей. Это деление учитывается также и неформально при дальнейшем применении или сравнении родственных эконометрических моделей.

При положительном ответе на вопрос о согласованности ранжировок результирующая (итоговая) ранжировка находится как эмпирическое среднее, т.е. медиана Кемени, согласно методам и алгоритмам статистики объектов нечисловой природы. При отрицательном ответе на вопрос о согласованности ранжировок результирующие (итоговые) ранжировки находятся отдельно для каждого кластера. При этом, например, констатируется принципиальное различие научных школ, к которым принадлежат эксперты.