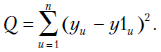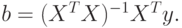|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Множественная регрессия
3.2. МНК-модель
Как было сказано, при использовании метода наименьших квадратов (МНК) минимизируется сумма квадратов остатков модели:
Для нахождения минимума вычисляются частные производные  функции
функции  по переменным
по переменным  , затем
, затем  приравнивают нулю. Получаем систему нормальных МНК-уравнений для определения оценок коэффициентов
приравнивают нулю. Получаем систему нормальных МНК-уравнений для определения оценок коэффициентов 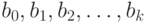 :
:
Примем за  вектор-столбец (
вектор-столбец ( , а за y вектор-столбец
, а за y вектор-столбец  . Тогда систему уравнений (3.6) можно представить в матричном виде
. Тогда систему уравнений (3.6) можно представить в матричном виде
Используя скалярные произведения векторов-столбцов 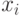 матрицы X, матрицу
матрицы X, матрицу  можно также записать в виде
можно также записать в виде
Предположим, что  имеет обратную матрицу
имеет обратную матрицу 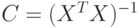 . Она называется матрицей дисперсий-ковариаций или просто ковариационной матрицей. Умножив уравнение (3.7) слева на матрицу
. Она называется матрицей дисперсий-ковариаций или просто ковариационной матрицей. Умножив уравнение (3.7) слева на матрицу  , получим
, получим
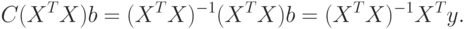
Поскольку (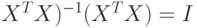 , формула для решения системы нормальных уравнений МНК принимает вид
, формула для решения системы нормальных уравнений МНК принимает вид
(Геометрическую интерпретацию метода наименьших квадратов см. в Приложении 3.)