|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Лабораторная работа № 3: Мультиколлинеарность
Отбор наиболее существенных объясняющих переменных
регрессионной модели
Исследуется зависимость урожайности зерновых культур УРОЖ (ц/га) от ряда переменных, характеризующих различные факторы сельскохозяйственного производства. Рассмотрены следующие факторы:
- ЧИС_ТРАК - число тракторов (приведенной мощности) на 100 га;
- ЧИС_КОМ - число зерноуборочных комбайнов на 100 га;
- ЧИС_ОР_П - число орудий поверхностной обработки почвы на 100 га;
- КОЛ_УДОБ - количество удобрений, вносимых на гектар (т/га);
- КОЛ_ХИМ - количество химических средств защиты растений, расходуемых на гектар (ц/га).
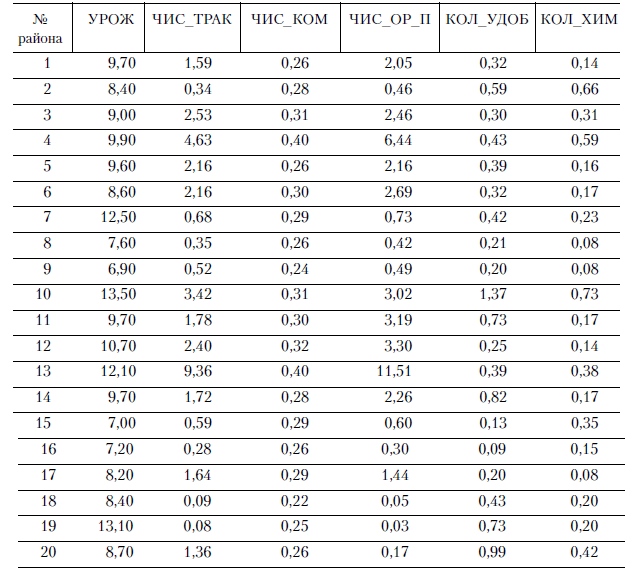
Исходные данные по 20 сельскохозяйственным районам приведены в табл. 1.
Таблица 1
Требуется исследовать зависимость урожайности от перечисленных факторов.
Для этого следует рассмотреть влияние на зависимую переменную всех переменных и, отобрав наиболее значимые, построить уравнение регрессии. В случае обнаружения мультиколлинеарности использовать методы, позволяющие уменьшить ее влияние.
Отчет по лабораторной работе № 3
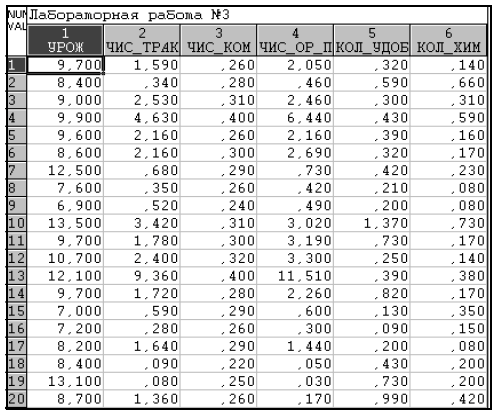
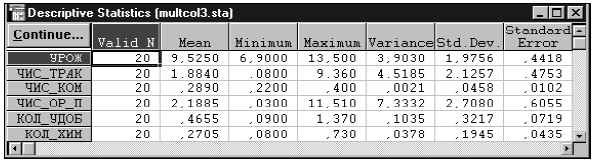
Представлены исходные данные (табл. 2), дескриптивные статистики (табл. 3) и матрица коэффициентов корреляции признаков (табл. 4).
Таблица 2
Таблица 3
Таблица 4
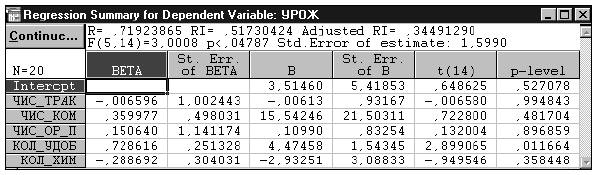
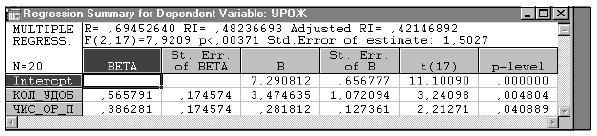
Уравнение множественной регрессии имеет вид
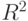 = 0,517.
= 0,517.
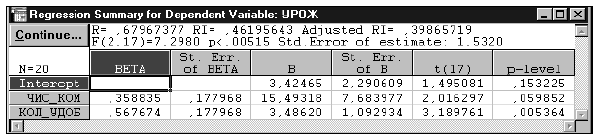
Полученное уравнение регрессии (табл. 5) значимо на стандартном 5%-ном уровне ( = 0,047) и объясняет примерно 52% вариации зависимой переменной при пяти объясняющих переменных, включенных в модель. Однако это уравнение не позволяет оценить вклад каждой входящей в него переменной, поскольку все они, кроме переменной КОЛ_УДОБ, не значимы. Такое положение является следствием мультиколлинеарности, вызванной тесной корреляционной связью между переменными регрессионного уравнения. В этом можно убедиться, анализируя матрицу парных коэффициентов корреляции (см. табл. 4).
= 0,047) и объясняет примерно 52% вариации зависимой переменной при пяти объясняющих переменных, включенных в модель. Однако это уравнение не позволяет оценить вклад каждой входящей в него переменной, поскольку все они, кроме переменной КОЛ_УДОБ, не значимы. Такое положение является следствием мультиколлинеарности, вызванной тесной корреляционной связью между переменными регрессионного уравнения. В этом можно убедиться, анализируя матрицу парных коэффициентов корреляции (см. табл. 4).
Для устранения мультиколлинеарности можно применить процедуру пошагового отбора переменных. Рассмотрим два подхода, реализованных в пакете STATISTICA:
- последовательного присоединения переменных (Forward stepwise);
- последовательного удаления (исключения) переменных (Baskward stepwise).
Таблица 5
На первом шаге процедуры Forward stepwise (табл. 6) в модель была включена переменная КОЛ_УДОБ, имеющая с результирующей переменной УРОЖ наибольший квадрат коэффициента корреляции - 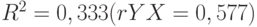 .
.
Таблица 6
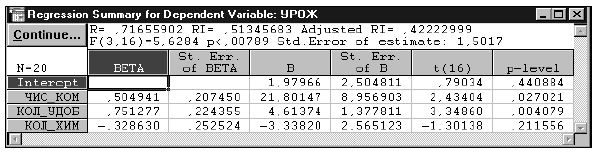
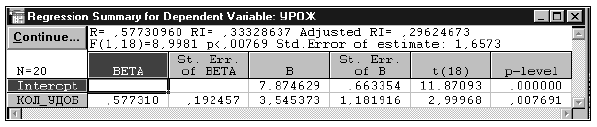
На втором шаге (табл. 7) добавлена переменная ЧИС_ОР_П. Полученное уравнение, также как и первое, значимо на стандартном 5%-ном уровне. Все коэффициенты входящих в уравнение переменных значимо отличны от нуля.
Таблица 7
Сравнивая полученное уравнение с предыдущим, отметим, что возросло не только значение коэффициента детерминации (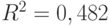 ), но и значение скорректированного коэффициента (
), но и значение скорректированного коэффициента ( ), что весьма существенно. При этом стандартные ошибки уравнений регрессии различаются мало - 1,6573 и 1,5027. Общий ход выполнения пошаговой процедуры включения отражен в табл. 8.
), что весьма существенно. При этом стандартные ошибки уравнений регрессии различаются мало - 1,6573 и 1,5027. Общий ход выполнения пошаговой процедуры включения отражен в табл. 8.
Таблица 8
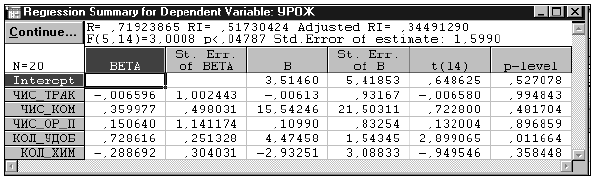
На шаге 0 пошаговой процедуры последовательного удаления (исключения) переменных (Backward stepwise) рассматривается уравнение регрессии, включающее весь набор исходных переменных (табл. 9).
Таблица 9
Все последующие шаги этой процедуры приведены в соответствующих таблицах:
шаг 1 - в табл. 10;
шаг 2 - в табл. 11;
шаг 3 - в табл. 12;
шаг 4 - в табл. 13.
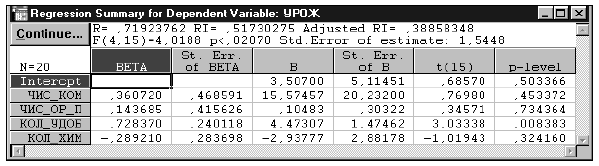
Таблица 10
Таблица 11
Таблица 12
Таблица 13
Общий ход выполнения пошаговой процедуры исключения отражен в табл. 14 и на рис. 1.
Таблица 14
На графике (см. рис. 1) представлены значения скорректированного коэффициента детерминации 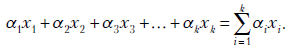 , полученные в ходе выполнения процедуры пошагового удаления переменных. Наилучшим вариантом следует признать тот, при котором достигается наибольшее значение скорректированного коэффициента детерминации, т.е. вариант, полученный на шаге 2. Это уравнение имеет вид:
, полученные в ходе выполнения процедуры пошагового удаления переменных. Наилучшим вариантом следует признать тот, при котором достигается наибольшее значение скорректированного коэффициента детерминации, т.е. вариант, полученный на шаге 2. Это уравнение имеет вид:
| УРОЖ = | 1,980 + | 21,801 ЧИС_КОМ + | 4,614 КОЛ_УДОБ - | 3,380 КОЛ_ХИМ, 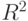 = 0,513. = 0,513. |
| (с. о) | (2,50) | (8,96) | (1,38) | (2,57) |
Стандартизированное уравнение регрессии для этого набора переменных выглядит следующим образом:
УРОЖ = 0,505 ЧИС_КОМ + 0,751 КОЛ_УДОБ - 0,329 КОЛ_ХИМ.
Анализ коэффициентов этого уравнения позволяет сравнить степени влияния на результирующий показатель объясняющих переменных. Так, влияние переменной КОЛ_УДОБ (количество удобрений, вносимых на гектар) на величину урожая при постоянных средних значениях других показателей примерно в 1,5 раза выше, чем переменной ЧИС_КОМ (число комбайнов). Влияние переменной КОЛ_ХИМ (количество химических средств защиты растений, расходуемых на гектар) интерпретировать не следует ввиду незначимости этого показателя в уравнении регрессии. Отметим, что при проведении пошаговой процедуры включения эта объясняющая переменная не была включена в регрессионную модель.
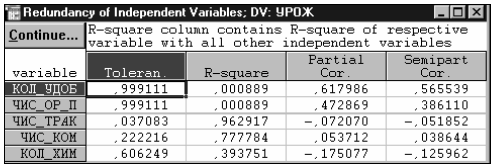
Результаты расчета коэффициентов толерантности и детерминации, полученные в ходе пошаговых процедур, представлены в табл. 15.
Таблица 15
Анализ табл. 15 позволяет судить об избыточности входящих в уравнение переменных. Так, две первые переменные довольно слабо связаны со всеми остальными. Об этом свидетельствует коэффициент множественной детерминации связи этих переменных со всем набором остальных переменных. И наоборот, последние три переменные имеют довольно тесную связь со всеми другими переменными, что и обусловливает наличие мультиколлинеарности ( ).
).
Аналогичный вывод позволяет сделать анализ частных коэффициентов корреляции (Partial Cor.). Первые две переменные имеют более тесную связь с зависимой переменной, чем остальные три переменные.