|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Опубликован: 26.07.2006 | Уровень: специалист | Доступ: платный
Лекция 12:
Нечеткие алгоритмы обучения
Моделируется поиск глобального экстремума функции следующим образом:
- область определения целевой функции делится на некоторое число подобластей (форма подобластей постоянно меняется) и описывается некоторым множеством точек;
- каждой точке приписывается состояние автомата, причем функция принадлежности в каждом состоянии указывает степень близости к оптимуму;
- выбирается состояние с максимальным значением функции принадлежности (эта точка называется кандидатом);
- формируется новая подобласть из точек, окружающих кандидата (размер подобласти растет, когда значение целевой функции в точке кандидата меньше, чем в других точках подобласти, и уменьшается в противоположном случае);
- когда подобласть пересекается с некоторой другой, или две точки-кандидаты находятся в одной подобласти, то подобласти разделяются, если степень разделения большая, или объединяются, если степень разделения малая;
- точки-кандидаты выбираются на этапе локального поиска в подобласти, затем во всей области среди точек-кандидатов ищется глобальная оптимальная точка;
- глобальный и локальный поиск осуществляется поочередно.
Алгоритм поиска глобального экстремума приведен на рис.12.2.
Пусть  — множество состояний,
— множество состояний,  —
выходной универсум,
—
выходной универсум,  —
функция выхода (функция принадлежности, указывающая степень
оптимума в состоянии
—
функция выхода (функция принадлежности, указывающая степень
оптимума в состоянии  ),
), 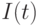 — текущее
значение целевой функции,
— текущее
значение целевой функции, 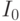 —
среднее значение
—
среднее значение 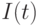 .
.
Используется следующий алгоритм изменения функций перехода и выхода в случае глобального поиска:
если 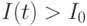 , то попытка успешна и
, то попытка успешна и

если 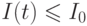 , то попытка неудачна и
, то попытка неудачна и

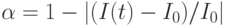 ;
;  — гарантируемая сходимость.
— гарантируемая сходимость.В случае локального поиска:
если 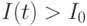 , то
, то

если 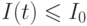 , то
, то


