Нечеткие алгоритмы

Обобщенная нечеткая машина определяется парой 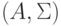, где — обобщенная машина, — конечное множество нечетких инструкций и каждая нечеткая инструкция из есть -функция из в .

Пусть задана некоторая обобщенная нечеткая машина 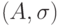. Выполнение последовательности 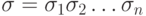на обобщенной машине есть последовательность

Весом, соответствующим выполнению, является элемент где

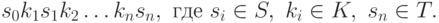
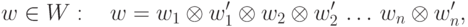
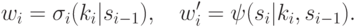
Выполнение возможно тогда и только тогда, если . Есл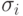и и принимают значения из различных множеств и , то вес, соответствующий выполнению, будет определяться парой . В этом случае говорят, что программа выполнима с весом 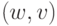, если .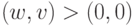

Пример. Пусть имеется последовательность инструкций для водителя автомобиля и карта местности. Водителю предлагается найти место назначения, используя карту и последовательность нечетких инструкций, описывающих маршрут. Для простоты изложения предположим, что все точки на плоскости имеют только целочисленные координаты. Типичные инструкции для водителя: "двигаться прямо около метров", "повернуть налево", "повернуть направо", "двигаться прямо до тех пор, пока не увидишь ...".

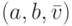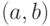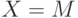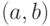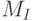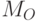Сконструируем соответствующую -машину . -машина имеет множество состояний памяти в виде упорядоченных троек , где — точка на плоскости, соответствующая местонахождению автомобиля, — единичный вектор направления движения автомобиля. Множество входов и множество выходов состоят из упорядоченных пар ; — функция входов, соответствует тождественной функции; — функция выходов, соответствует функции, отображающей каждую тройку 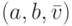в .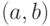

Машина не имеет ни одной функции условия. Каждой инструкции, приведенной выше, соответствует функция операции. При этом -я инструкция в последовательности инструкций может быть преобразована в инструкцию операции вида do 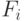; go to 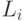. Совокупность таких инструкций и инструкций start: go to 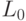и 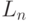: halt, где — длина последовательности, составляет программу . Процесс выполнения программы на машине определяется последовательностью инструкций и картой местности. Краткости ради приведем только функцию операции для инструкции типа "двигаться прямо около метров":

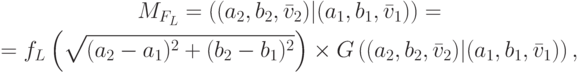
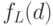где — степень (вес), соответствующая расстоянию , 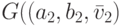| 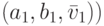— вес, соответствующий утверждению: "точка 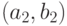и направление 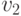достижимы при движении прямо из точки 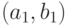по направлению ".

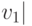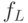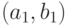Примеры функций и , где — параметр: тогда и только тогда, если вектор из в 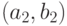параллелен и каждая точка на отрезке линии, проходящей через 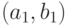и 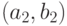, имеющая целые координаты, есть точка на карте. Очевидно, что 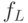зависит только от , а зависит только от карты. Другие функции операций могут быть построены аналогично. Нечеткий алгоритм, описывающий движение автомобиля к месту назначения, определяется конкретной последовательностью инструкций приведенного вида, которая реализуется на рассмотренной -машине.

Приведем другие примеры применения нечетких алгоритмов.

• Алгоритмы определения сложного нечеткого понятия через более простые понятия, которые легко описать нечеткими множествами; результатом применения таких алгоритмов к некоторому элементу области рассуждений будет степень принадлежности понятию (степень, с которой элемент может характеризоваться понятием );
• Алгоритмы порождения, в результате выполнения которых порождается один из элементов нечеткого множества, которое описывает интересующее нас понятие (например, алгоритм порождения образцов почерка, рецептов приготовления пищи, сочинения музыки, предложений в естественном языке);
• Алгоритмы описания отношений между нечеткими переменными, например, в виде последовательности нечетких инструкций типа: "если мало и увеличить слегка, то увеличится слабо"; такие алгоритмы позволяют приближенно описывать поведение систем, входные и выходные сигналы которых являются нечеткими подмножествами;
• Алгоритмы принятия решения, позволяющие приближенно описывать стратегию или важнейшее правило, например, алгоритм проезда перекрестка, содержащий последовательность действий, которые необходимо выполнить, при этом описания этих действий состоят из нечетких понятий типа: нормальная скорость, несколько секунд, медленно приближаться.