|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие алгоритмы
Способы выполнения нечетких алгоритмов
Для реализации поиска какого-либо выполнения нечеткого алгоритма 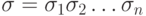 необходимо определить правила выбора машинной инструкции на каждом шаге.
Правила выбора машинной инструкции и переходов из состояния в состояние
зависят от типа нечеткой машины.
необходимо определить правила выбора машинной инструкции на каждом шаге.
Правила выбора машинной инструкции и переходов из состояния в состояние
зависят от типа нечеткой машины.
Выбор машинной инструкции:
a. Нечеткий выбор. Машина выбирает машинную
инструкцию 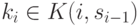 с наивысшей степенью на каждом
шаге
с наивысшей степенью на каждом
шаге 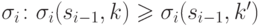 для любой инструкции
для любой инструкции 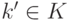 .
.
b. Вероятностный выбор. Машина на каждом шаге нечеткой
инструкции 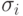 выбирает
инструкцию
выбирает
инструкцию 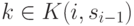 с вероятностью
с вероятностью  ,
пропорциональной нечеткой
степени
,
пропорциональной нечеткой
степени 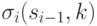
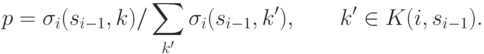
c. Недетерминированный выбор. Машинная инструкция 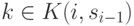 выбирается недетерминированным образом.
выбирается недетерминированным образом.
Определение перехода из состояния в состояние:
a. Нечеткий переход. Машина переходит из состояния 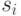 в состояние
в состояние 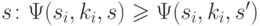 для любого
состояния
для любого
состояния 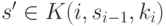 .
.
b. Вероятностный переход. Машина переходит из состояния 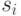 в состояние
в состояние  с вероятностью
с вероятностью
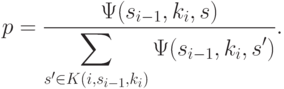
c. В случае детерминированного перехода состояние, пригодное для
машины, единственным образом определяется функцией
переходов  .
.
Процедура возврата:
a. Вернуться на предыдущую нечеткую инструкцию.
b. Вернуться на нечеткую инструкцию, соответствующую машинной инструкции с наивысшей функцией принадлежности в ряде таких инструкций, просмотренных последовательно до выбранной нечеткой инструкции.
c. Осуществить возврат так же, как описано в пункте (b), но при этом машинная инструкция выбирается со степенью более высокой, чем выбранная перед этим.
Представление нечеткого алгоритма в виде графа
Во многих случаях нечеткий алгоритм удобно представлять в виде ориентированного графа. Каждой дуге ставят в соответствие инструкцию условия или инструкцию операции. Входные, выходные, внутренние переменные в нечетком алгоритме представляются нечеткими множествами. Выполнение алгоритма эквивалентно поиску в графе путей, связывающих помеченные вершины: начальные и конечные. Приведем необходимые для дальнейшего изложения известные определения графа и путей в графе.
Определение.
Графом  называется тройка
называется тройка 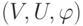 , где
, где 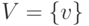 — множество
элементов, называемых вершинами графа;
— множество
элементов, называемых вершинами графа; 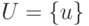 множество
элементов,
называемых ребрами графа, причем
множество
элементов,
называемых ребрами графа, причем 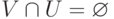 ;
;  —
функция, ставящая в соответствие каждому ребру
—
функция, ставящая в соответствие каждому ребру 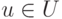 упорядоченную или неупорядоченную
пару вершин
упорядоченную или неупорядоченную
пару вершин 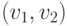 ,
, 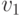 и
и 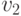 называются концами ребра
называются концами ребра  .
Если множество
.
Если множество 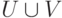 конечно, то граф называется конечным.
Если
конечно, то граф называется конечным.
Если 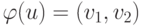 — упорядоченная пара (т.е.
— упорядоченная пара (т.е.  ),
то ребро
),
то ребро  называется ориентированным ребром или дугой,
исходящей из вершины
называется ориентированным ребром или дугой,
исходящей из вершины 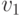 и входящей в вершину
и входящей в вершину 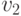 ;
; 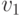 называется началом,
называется началом, 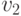 — концом дуги
— концом дуги  . Граф, все ребра
которого ориентированные, называется
ориентированным графом.
. Граф, все ребра
которого ориентированные, называется
ориентированным графом.
Определение.
Последовательность вершин и ребер графа 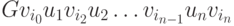 называется путем
называется путем ![\([v_{i{}_0} ,v_{i_n } ]\)](/sites/default/files/tex_cache/12b4cef735f43a18bb0d85f670643db8.png) из вершины
из вершины 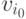 в вершину
в вершину 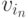 , если
, если 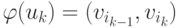 для
для 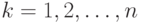 . Вершина
. Вершина 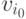 называется
началом, а
называется
началом, а 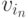 — концом пути; число
— концом пути; число  называется длиной пути.
называется длиной пути.
Определение. Нечеткая
программа есть четверка 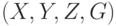 , где
, где 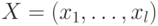 — вектор
входа,
— вектор
входа, 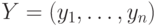 — вектор программы (внутренние
переменные),
— вектор программы (внутренние
переменные), 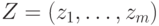 — вектор выхода,
— вектор выхода,  — ориентированный
граф:
— ориентированный
граф:
-
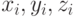 — нечеткие переменные, определяющие
нечеткие множества на
— нечеткие переменные, определяющие
нечеткие множества на 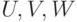 ;
; - В графе
 существует точно одна вершина, называемая начальной
(стартовой), которая не является конечной вершиной никакой дуги, и существует точно одна вершина, называемая конечной (финальной), которая не является начальной вершиной никакой дуги: любая вершина графа находится на некотором пути
из стартовой вершины
существует точно одна вершина, называемая начальной
(стартовой), которая не является конечной вершиной никакой дуги, и существует точно одна вершина, называемая конечной (финальной), которая не является начальной вершиной никакой дуги: любая вершина графа находится на некотором пути
из стартовой вершины  в финальную вершину
в финальную вершину  ;
; - В графе
 любая дуга
любая дуга  , не ведущая в
, не ведущая в  , связана с нечетким отношением
, связана с нечетким отношением 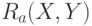 и нечеткой инструкцией
и нечеткой инструкцией 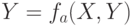 ; каждая дуга
; каждая дуга  , ведущая в
, ведущая в  , связана с нечетким
отношением
, связана с нечетким
отношением 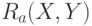 и инструкцией
и инструкцией  , где
, где  —
нечеткое отношение, и
—
нечеткое отношение, и  — нечеткая операция типа
пересечения, объединения, отрицания нечеткой арифметики, оператор размывания,
оператор типа модификаторов и т.д.
— нечеткая операция типа
пересечения, объединения, отрицания нечеткой арифметики, оператор размывания,
оператор типа модификаторов и т.д.
