Трансформации

Таблица 6.7. Таблица 6.7 Команда MatrixTransform для нескольких преобразований

№	Код	Вид в браузере
6.7.1
	<Canvas xmlns="http://schemas.microsoft.com/client/2007" xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml" Width="200" Height="200" Background="White" x:Name="Page"> <!--Исходная фигура--> <Rectangle Canvas.Left="10" Canvas.Top="10" Width="100" Height="50" Fill="yellow" Stroke="red" StrokeThickness="4"/> <Rectangle Canvas.Left="10" Canvas.Top="10" Width="50" Height="25" Fill="green" Stroke="red" StrokeThickness="4" /> <!--Трансформированная фигура --> <Canvas Width="200" Height="200" Canvas.Left="0" Canvas.Top="0"> <Rectangle Canvas.Left="10" Canvas.Top="10" Width="100" Height="50" Fill="yellow" Stroke="red" StrokeThickness="4"/> <Rectangle Canvas.Left="10" Canvas.Top="10" Width="50" Height="25" Fill="green" Stroke="red" StrokeThickness="4" /> <Canvas.RenderTransform> <MatrixTransform Matrix="1 0 1 1 -10 0"/> <!--<SkewTransform AngleX="45" /> <TranslateTransform X="-10" Y="0"/> --> </Canvas.RenderTransform> </Canvas> </Canvas>
	Описание
	Преобразование состоит из двух команд. Запишем их отдельные матрицы: TranslateTransform X="-10" Y="0": SkewTransform AngleX="45": Вычисляем произведение матриц: 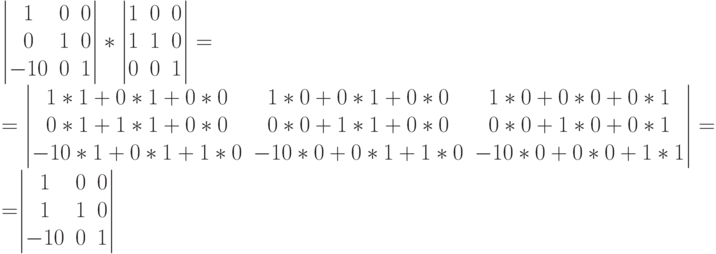tg(45)=1 Результирующая команда: Matrix="1 0 1 1 -10 0"

Запись серии команд в виде матрицы позволяет сократить запись и, следовательно, уменьшить размер XAML – документа.

Вычисление матриц может показаться сложно задачей, существенно затрудняющей создание пользовательского интерфейса приложения. Однако для перемножения матриц в C# уже есть встроенные методы и классы. Типичный фрагмент кода для получения результирующей матрицы записывается достаточно лаконично:

private void multiplicationExample()
{

    Matrix matrix1 = new Matrix(5, 10, 15, 20, 25, 30);
    Matrix matrix2 = new Matrix(2, 4, 6, 8, 10, 12);

    // matrixResult is equal to (70,100,150,220,240,352) 
    Matrix matrixResult = Matrix.Multiply(matrix1, matrix2);

    // matrixResult2 is also
    // equal to (70,100,150,220,240,352) 
    Matrix matrixResult2 = matrix1 * matrix2;

}

Готовая матрица может быть связана с графическим объектом на стадии выполнения кода.

Вычисление матриц в программе Mathcad

Для вычисления матриц может применяться еще одно средство, позволяющее весьма наглядно понять логику работы. Пакет Mathcad (http://www.ptc.com/go/mathsoft) – мощное средство для решения широкого класса вычислительных задач, содержит удобные инструменты для работы с матрицами. После установки и запуска программы можно сразу приступать к вычислениям. В главном меню выбираем "Insert – Matrix" ( или нажимаем Ctrl+M) (рис. 6.12):

увеличить изображение
Рис. 6.12. Вставка матрицы

В появившемся диалоговом окне выбираем матрицы размером 3х3 (рис.6.13 ):

Рис. 6.13. Определение размера матрицы

В документе появляется шаблон, в который можно вводить числа (рис. 6.14):

Рис. 6.14. Шаблон матрицы

После завершения ввода вводим знак равенства "=" и программа автоматически отображает результирующую матрицу (рис. 6.15):

увеличить изображение
Рис. 6.15. Готовые матрицы

Программа поддерживает также вычисление тригонометрических функций, которые можно задавать непосредственно в текстовом виде.