Основы XAML

:

Основы XAML
[+]
Опубликован: 23.01.2009 | Уровень: для всех | Доступ: платный
Лекция 6:

Трансформации
A
|
версия для печати
< Лекция 5 || Лекция 6: 1234567 || Лекция 7 >

MatrixTransform

Трансформация MatrixTransform представляет собой способ компактной записи серии преобразований. Графически эта команда не содержит собственных изменений объекта. Она лишь выражает применение одной или нескольких команд типа RotateTransform, SkewTransform, ScaleTransform и TranslateTransform. Математически, все преобразования могут быть выражены в виде матрицы третьего порядка следующим образом:

$$\begin{vmatrix} M_{11}&M_{12}& 0\\ M_{21}&M_{22}&0\\ OffsetX&OffsetY&1 \end{vmatrix}$$

Команда будет выглядеть так:

(M11, M12, M21, M22, OffsetX, OffsetY)

Каждое из преобразований представляется своей матрицей и соответствующей командой MatrixTransform.

Команда TranslateTransform:

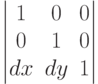
$$\begin{vmatrix} 1&0&0\\ 0&1&0\\ dx&dy&1 \end{vmatrix}$$ 
Matrix="1 0 0 1 dx dy"

Команда RotateTransform:

$$\begin{vmatrix} cos(a)&sin(a)&0\\ -sin(a)&cos(a)&0\\ 0&0&1 \end{vmatrix}$$ 
Matrix=" cos(a) sin(a) –sin(a) cos(a) 0 0"

Команда ScaleTransform:

$$\begin{vmatrix} sx&0&0\\ 0&sy&0\\ 0&0&1 \end{vmatrix}$$ 
Matrix=" sx 0 0 sy 0 0"

Команда SkewTransform (AngleX):

$$\begin{vmatrix} 1&0&0\\ tg(a)&1&0\\ 0&0&1 \end{vmatrix}$$ 
Matrix="1 0 tg(a) 1 0 0"

Команда SkewTransform (AngleY):

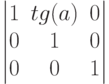
$$\begin{vmatrix} 1&tg(a)&0\\ 0&1&0\\ 0&0&1 \end{vmatrix}$$ 
Matrix="1 tg(a) 0 1 0 0"

Практически, для перехода к новой форме записи нужно просто взять исходные параметры команды и аккуратно их подставить в нужные позиции. Для команд RotateTransform, SkewTransform (AngleX) и SkewTransform (AngleY) дополнительно следует вычислить тригонометрические функции углов. В табл. 6.6 приводятся примеры использования этой записи.

Таблица 6.6. Команда MatrixTransform
№ Код Вид в браузере
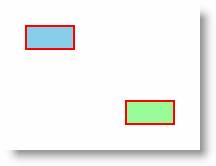
6.6.1
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="150"
Background="White"
x:Name="Page">
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" 
Height="25"  Fill="skyblue" 
Stroke="red" StrokeThickness="2"/>
  
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" 
Height="25"  Fill="palegreen" 
Stroke="red" StrokeThickness="2"
 RenderTransformOrigin="0.5,0.5">
  <Rectangle.RenderTransform>    
        
  <MatrixTransform Matrix="1 0 0 1 100 75"/>
    <!--<TranslateTransform X="100" 
Y="75"/>-->
  </Rectangle.RenderTransform>
</Rectangle>
  
</Canvas>

Описание
Запись команды TranslateTransform в форме MatrixTransform
№ Код Вид в браузере
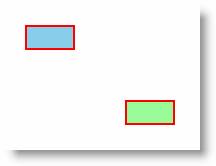
6.6.2
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="150"
Background="White"
x:Name="Page">
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" 
Height="25"  Fill="skyblue" 
Stroke="red" StrokeThickness="2"/>
  
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" 
Height="25"  Fill="palegreen" 
Stroke="red" StrokeThickness="2" 
RenderTransformOrigin="0.5,0.5">
  <Rectangle.RenderTransform>    
  <MatrixTransform x:Name="my
MatrixTransform">
           <MatrixTransform.Matrix >
    <Matrix M11="1" 
M12="0" M21="0" M22="1"  
OffsetX="100" OffsetY="75"/>
    <!--<TranslateTransform X="100" 
Y="75"/>-->
     </MatrixTransform.Matrix>
         </MatrixTransform>
  </Rectangle.RenderTransform>
</Rectangle>
  
</Canvas>

Описание
Задание атрибута x:Name позволяет обращаться к преобразованию программным способом. Кроме того, здесь, в отличие от предыдущего примера используется запись в виде тегов
№ Код Вид в браузере
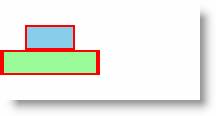
6.6.3
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="100"
Background="White"
x:Name="Page">
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" 
Height="25"  Fill="skyblue" 
Stroke="red" StrokeThickness="2"/>
  
<Rectangle Canvas.Left="25" 
Canvas.Top="50" Width="50" 
Height="25"  Fill="palegreen" 
Stroke="red" StrokeThickness="2" 
RenderTransformOrigin="0.5,0.5">
  <Rectangle.RenderTransform>    
        
   <MatrixTransform Matrix="2 0 0 1 0 0"/>
   <!--<ScaleTransform ScaleX="2" 
ScaleY="1"  />  -->
  </Rectangle.RenderTransform>
</Rectangle>
  
</Canvas>

Описание
Запись команды ScaleTransform в форме MatrixTransform. Заметно смещение фигуры по сравнению с результатом, получаемым применением команды ScaleTransform
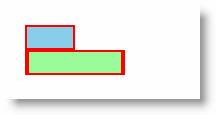
№ Код Вид в браузере
6.6.4
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="100"
Background="White"
x:Name="Page">
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" Height="25"  
Fill="skyblue" Stroke="red" 
StrokeThickness="2"/>
  
<Rectangle Canvas.Left="25" 
Canvas.Top="50" Width="50" 
Height="25"  Fill="palegreen" 
Stroke="red" StrokeThickness="2" 
RenderTransformOrigin="0.5,0.5">
  <Rectangle.RenderTransform>    
          
    <MatrixTransform Matrix="2 0 0 1 25 0"/>
    <!--<ScaleTransform ScaleX="2" 
ScaleY="1"  />  -->
  </Rectangle.RenderTransform>
</Rectangle>
  
</Canvas>

Описание
Запись команды ScaleTransform в форме MatrixTransform. Для компенсации смещения указывается величина смещения, равная 25. Фактически, две последние цифры в значении атрибута Matrix – это смещение по горизонтали и вертикали
№ Код Вид в браузере
6.6.5
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="100"
Background="White"
x:Name="Page">
<Rectangle Canvas.Left="25" 
Canvas.Top="25" Width="50" 
Height="25"  Fill="skyblue" 
Stroke="red" StrokeThickness="2"/>
  
<Rectangle Canvas.Left="25" 
Canvas.Top="50" Width="50" 
Height="25"  Fill="palegreen" 
Stroke="red" StrokeThickness="2" 
RenderTransformOrigin="0.5,0.5">
  <Rectangle.RenderTransform>    
          
    <MatrixTransform x:Name="
myMatrixTransform">
           <MatrixTransform.Matrix >
    <Matrix M11="2" M12="0" 
M21="0" M22="1"  OffsetX="25" 
OffsetY="0"/>
    <!--<ScaleTransform ScaleX="2" 
ScaleY="1"  />  -->
     </MatrixTransform.Matrix>
         </MatrixTransform>    
  </Rectangle.RenderTransform>
</Rectangle>
  
</Canvas>

Описание
Запись команды ScaleTransform в форме MatrixTransform. Matrix превращается в тег, для которого указываются набор атрибутов. Здесь явно видно, что OffsetX и OffsetY определяют трансляцию (перенос) фигуры
№ Код Вид в браузере
6.6.6
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="210" Height="210"
Background="White"
x:Name="Page">
<!--Исходная фигура-->
<Rectangle Canvas.Left="105" 
Canvas.Top="4" Width="100" 
Height="50"  Fill="yellow" 
Stroke="red" StrokeThickness="4"/>
<Rectangle Canvas.Left="105" 
Canvas.Top="4" Width="50"
 Height="25"  Fill="green" 
Stroke="red" StrokeThickness="4" />

<!--Повернутая фигура-->  
<Canvas Width="210" Height="210" 
Canvas.Left="0" Canvas.Top="0">
<Rectangle Canvas.Left="105" 
Canvas.Top="4" Width="100" 
Height="50"  Fill="yellow" 
Stroke="red" StrokeThickness="4"/>
<Rectangle Canvas.Left="105" 
Canvas.Top="4" Width="50"
 Height="25"  Fill="green" 
Stroke="red" StrokeThickness="4" />

  <Canvas.RenderTransform>
    <MatrixTransform Matrix="0.7071 
0.7071 -0.7071 0.7071 0 0"/>    
    <!--<RotateTransform 
Angle="45"/>-->    
  </Canvas.RenderTransform>
  </Canvas>
</Canvas>

Описание
Запись команды RotateTransform в форме MatrixTransform
№ Код Вид в браузере
6.6.7
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="200"
Background="White"
x:Name="Page">
<!--Исходная фигура-->
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="100" 
Height="50"  Fill="yellow" 
Stroke="red" StrokeThickness="4"/>
<Rectangle Canvas.Left="10" Canvas.Top="10" 
Width="50" Height="25"  Fill="green" 
Stroke="red" StrokeThickness="4" />

<!--Трансформированная фигура -->
<Canvas Width="200" Height="200" 
Canvas.Left="0" Canvas.Top="0">
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="100" 
Height="50"  Fill="yellow"
 Stroke="red" StrokeThickness="4"/>
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="50" 
Height="25"  Fill="green" 
Stroke="red" StrokeThickness="4" />

  <Canvas.RenderTransform>    
  <MatrixTransform Matrix="1 0 1 1 0 0"/>  
    <!--<SkewTransform AngleX=
"45" />  -->
  </Canvas.RenderTransform>
  </Canvas>
</Canvas>

Описание
Запись команды SkewTransform в форме MatrixTransform. tg(45)=1
№ Код Вид в браузере
6.6.8
<Canvas
xmlns="http://schemas.microsoft.com/client/2007"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Width="200" Height="200"
Background="White"
x:Name="Page">
<!--Исходная фигура-->
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="100" 
Height="50"  Fill="yellow" 
Stroke="red" StrokeThickness="4"/>
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="50" 
Height="25"  Fill="green" 
Stroke="red" StrokeThickness="4" />

<!--Трансформированная фигура -->
<Canvas Width="200" Height="200" 
Canvas.Left="0" Canvas.Top="0">
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="100" 
Height="50"  Fill="yellow" 
Stroke="red" StrokeThickness="4"/>
<Rectangle Canvas.Left="10" 
Canvas.Top="10" Width="50" 
Height="25"  Fill="green" 
Stroke="red" StrokeThickness="4" />

  <Canvas.RenderTransform>  
  <TransformGroup>  
  <MatrixTransform Matrix="1 1 0 1 0 0"/>  
    <!--<SkewTransform AngleY="45" />-->      
  </TransformGroup>  
  </Canvas.RenderTransform>
  </Canvas>
</Canvas>

Описание
Запись команды SkewTransform в форме MatrixTransform. tg(45)=1

Мы разобрали запись в виде матрицы отдельных команд. Немного более сложно обстоят дела с записей нескольких команд, например, TranslateTransform и SkewTransform в виде одной матрицы. Результирующая матрица представляет собой произведение отдельных матриц. Рассмотрим для начала произведение матриц, содержащих по две строки и два столбца:

$$ \begin{vmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{vmatrix}* \begin{vmatrix} b_{11}&b_{12}\\ b_{21}&b_{22} \end{vmatrix}= \begin{vmatrix} a_{11}*b_{11}+a_{12}*b_{21}&a_{11}*b_{12}+a_{12}*b_{22}\\ a_{21}*b_{11}+a_{22}*b_{21}&a_{21}*b_{12}+a_{22}*b_{22} \end{vmatrix}$$

Обратите внимание на индексы – индекс 12, к примеру, означает, что элемент b12 находится в первой строке и втором столбце. Результирующая матрица получается сложением и умножением отдельных элементов по следующей схеме (рис. 6.10):

Умножение матриц второго порядка

Рис. 6.10. Умножение матриц второго порядка

Аналогичным образом осуществляется умножение матриц третьего порядка:

$$ \begin{vmatrix} a_{11}&a_{12}&a_{13\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{vmatrix}* \begin{vmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33} \end{vmatrix}=\\= \begin{vmatrix} a_{11}*b_{11}+a_{12}*b_{21}+a_{13}*b_{31}&a_{11}*b_{12}+a_{12}*b_{22}+a_{13}*b_{32}&a_{11}*b_{13}+a_{12}*b_{23}+a_{13}*b_{33}\\ a_{21}*b_{11}+a_{22}*b_{21}+a_{23}*b_{31}&a_{21}*b_{12}+a_{22}*b_{22}+a_{23}*b_{32}&a_{21}*b_{13}+a_{22}*b_{23}+a_{23}*b_{33}\\ a_{31}*b_{11}+a_{32}*b_{21}+a_{33}*b_{31}&a_{31}*b_{12}+a_{32}*b_{22}+a_{33}*b_{32}&a_{31}*b_{13}+a_{32}*b_{23}+a_{33}*b_{33} \end{vmatrix}$$

Для отдельного элемента результирующей матрицы, находящегося во второй строке первого столбца можно выделить схему (рис. 6.11):

Умножение матриц третьего порядка

Рис. 6.11. Умножение матриц третьего порядка

Итак, для получения результирующей матрицы нескольких команд нужно записать отдельные матрицы, а затем их перемножить. В табл. 6.7 приведены примеры подобных матриц.

Дальше >>
< Лекция 5 || Лекция 6: 1234567 || Лекция 7 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 14
Илья Столупин
Илья Столупин
Россия
предложить дружбу
Олег Борхаленко
Олег Борхаленко
Украина
предложить дружбу