НОУ ИНТУИТ | Моделирование систем. Лекция 2: Моделирование многоканальных систем массового обслуживания

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 30.11.2010 | Уровень: специалист | Доступ: платный | ВУЗ: Мордовский государственный университет имени Н.П. Огарева

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать программу

Практическая часть

Пример 3. Для системы массового обслуживания 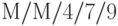М/М/4/7/9 постройте переходные вероятности состояний и определите для нее операционные характеристики при следующих параметрах: 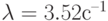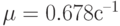$\lambda = 3.52 с^{–1}$ , $\mu = 0.678 с^{–1}$ . Среда программирования — MATLAB.

Запишем с буквенными коэффициентами дифференциальные уравнения для системы 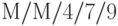М/М/4/7/9 :

$\frac{dP_{0}}{dt}=-M\lambda P_{0}+\mu P_{1},\\ \frac{dP_{1}}{dt}=M\lambda P_{0}-[(M-1)\lambda +\mu] P_{1}+2\mu P_{2},\\ \frac{dP_{2}}{dt}=(M-1)\lambda P_{1}-[(M-2)\lambda +2\mu] P_{2}+3\mu P_{3},\\ \frac{dP_{3}}{dt}=(M-2)\lambda P_{2}-[(M-3)\lambda +3\mu] P_{3}+4\mu P_{4},\\ \frac{dP_{4}}{dt}=(M-3)\lambda P_{3}-[(M-4)\lambda +4\mu] P_{4}+4\mu P_{5},\\ \frac{dP_{5}}{dt}=(M-4)\lambda P_{4}-[(M-5)\lambda +4\mu] P_{5}+4\mu P_{6},\\ \frac{dP_{6}}{dt}=(M-5)\lambda P_{5}-[(M-6)\lambda +4\mu] P_{6}+4\mu P_{7},\\ \frac{dP_{7}}{dt}=[M-(K-1)]\lambda P_{6}-4\mu P_{7},\\$

где:

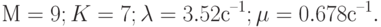
$М = 9; K = 7; \lambda = 3.52 с^{–1}; \mu = 0.678 с^{–1}.$

Полученную систему представим в матричном виде:

$\frac{dP}{dt}=AP,$

где матрица размера $8\times 8$ составляется из коэффициентов при вероятностях в правой части уравнений.

Для интегрирования дифференциальных уравнений примем естественные граничные условия.

Программный код решения примера в MATLAB:

function MMmKM;
clc,close all
% Параметры системы M/M/4/7/9
L = 2.2;
M = 3.678;
m = 4;
K = 7;
N = 9; 
% Матрица коэффициентов А
global A
A = [-N*L,M,zeros(1,6);
N*L,-[(N-1)*L+M],2*M,zeros(1,5);
zeros(1,1),(N-1)*L,-[(N-2)*L+2*M],3*M,zeros(1,4);
zeros(1,2),(N-2)*L,-[(N-3)*L+3*M],4*M,zeros(1,3);
zeros(1,3),(N-3)*L,-[(N-4)*L+4*M],4*M,zeros(1,2);
zeros(1,4),(N-4)*L,-[(N-5)*L+4*M],4*M,zeros(1,1);
zeros(1,5),(N-5)*L,-[(N-6)*L+4*M],4*M;
zeros(1,6),(N-6)*L,-4*M];
 
T = [0,2]; %% интервал интегрирования
P0 = [1,zeros(1,length(A)-1)]; %% начальные условия
[t,P] = ode23(@cmo,T,P0);
 
%% Построение диаграмм вероятностей состояний
% line(t,P,'linew',2) %% сплошные линии с различными цветами
line(t,P(:,1),'linew',2, 'color','r') %% Po
line(t,P(:,2), 'linew',2,'lines','--') %% P1
line(t,P(:,3), 'linew',2,'lines','-.') %% P2
line(t,P(:,4), 'linew',2,'lines',':') %% P3
line(t,P(:,5), 'marker','o', 'color', 'm') %% P4
line(t,P(:,6), 'marker','h', 'color','k') %% P5
line(t,P(:,7), 'marker','p','color','r') %% P6
line(t,P(:,8), 'marker','>') %% P7
grid on
Na = length(A) - 1;
arr = [0:Na]';
str = num2str(arr);
legend(strcat('\bf\itP\rm\bf_', str, '(\itt\rm\bf)'));

title(sprintf('%sСистема M/M/%d/%d/%d; %s%g; %s%g',...
'\bf\fontsize{11}',m,K,N,'\lambda = ',L,'\mu = ',M));
xlabel('\bf\it\fontsize{12} -  -  -  -  -  -  -  -   t   -  -  -  -  -  -  -  -');
ylabel('\bf\fontsize{12}\itP\rm\bf(\itt\rm\bf)');
set(gca, 'fontweight','bold', 'fontsize',10)
 
Pcm = P(end,:); % Стационарные вероятности
fprintf('\n Стационарные вероятности системы M/M/%d/%d/%d:\n', m,K,N);
for J = 1 : length(A)
    fprintf('\tP%d = %f\n', J-1, Pcm(J));
end
fprintf('\n ОПЕРАЦИОННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ M/M/%d/%d/%d:\n', m,K,N);
Pnot = P(end,end);
fprintf(' Вероятность отказа Pnot = %f\n', P(end,end));
Q = 1 - Pnot;
fprintf(' Относительная пропускная способность Q = %f\n', Q);
Ab = L*Q;
fprintf(' Абсолютная пропускная способность A = %f\n', Ab);
Pq = sum(P(end, m+1:end));
fprintf(' Вероятность наличия очереди Pq = %f\n', Pq);
Ps = sum(P(end, m:end));
fprintf(' Вероятность загрузки всех каналов обслуживания Ps = %f\n', Ps);
Ns = [0:length(A)-1]*P(end,:)';
fprintf(' Среднее количество требований в системе Ns = %f\n', Ns);
fprintf(' Среднее время пребывания требования в системе Ts = %f\n', Ns/L);
Nq = [0:(K-m)]*P(end,m:K)';
fprintf(' Средняя длина очереди Nq = %f\n', Nq);
fprintf(' Среднее время пребывания требования в очереди Tq = %f\n', Nq/L);
 
function f = cmo(t,P)
% М-функция описания правых частей дифференциальных уравнений:
global A
f = A*P;

Результат выполнения программы

Стационарные вероятности системы M/M/4/7/9:
	P0 = 0.013187
	P1 = 0.070956
	P2 = 0.169841
	P3 = 0.236851
	P4 = 0.212652
	P5 = 0.158847
	P6 = 0.095048
	P7 = 0.042619

 ОПЕРАЦИОННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ M/M/4/7/9
 Вероятность отказа: Pnot = 0.042619
 Относительная пропускная способность: Q = 0.957381
 Абсолютная пропускная способность: A = 2.106238
 Вероятность наличия очереди: Pq = 0.509166
 Вероятность загрузки всех каналов обслуживания: Ps = 0.746017
 Среднее количество требований в системе: Ns = 3.634652
 Среднее время пребывания требования в системе: Ts = 1.652115
 Средняя длина очереди: Nq = 0.815489
 Среднее время пребывания требования в очереди: Tq = 0.370677

Зависимости вероятностей состояний от времени показаны на рис. 2.6.

Рис. 2.6. Изменение вероятностей состояний во времени системы М/М/4/7/9

Задание 5

Рассчитайте стационарные вероятности по аналитическим формулам (см. теоретическую часть). Сравните результаты.
Постройте зависимость среднего времени пребывания в очереди от интенсивности входного потока, изменяя интенсивность от 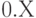до , где — номер компьютера (1, 2, 3, ...), за которым выполняется лабораторная работа.
Напишите программу для анализа системы с параметрами, вводимыми с клавиатуры пользователем, т. е. 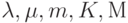$\lambda, \mu, m, K, М$ . Предусмотрите также ввод интервала интегрирования дифференциальных уравнений.

Контрольные вопросы

Что называется простейшим пуассоновским потоком?
По какому закону распределены интервалы времени между требованиями в простейшем пуассоновском потоке?
Что такое символика Кендалла, применяемая для систем массового обслуживания?
Что определяет собой точка на графике функции распределения случайной величины?
Какие случайные величины в системе массового обслуживания являются дискретными, а какими непрерывными?
Что означает несовместность событий?
Каким условиям должны отвечать начальные условия при решении дифференциальных уравнений относительно вероятностей состояния системы массового обслуживания?
Какова длина очереди в системе ?
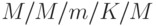Через какой тип данных могут выражаться интенсивность входного потока требований и интенсивность обслуживания требований в системах массового обслуживания?

Дальше >>

Моделирование систем

Моделирование систем

Моделирование многоканальных систем массового обслуживания

Практическая часть

Контрольные вопросы

Вопросы и ответы

Студенты

Авторизоваться

Моделирование систем

Моделирование систем

Моделирование многоканальных систем массового обслуживания

Практическая часть

Контрольные вопросы

Вопросы и ответы

Студенты