Лекция 10: Многометрическая (многомерная) оптимизация. Методы многомерной оптимизации: метод Хука – Дживса, метод Нелдера – Мида, метод полного перебора, метод покоординатного спуска, метод градиентного спуска

5. Метод градиентного спуска

Рассмотрим функцию f считая для определенности, что она зависит от трех переменных х, у, z. Вычислим ее частные производные df/dx, df/dy, df/dz и образуем с их помощью вектора, который называют градиентом функции:

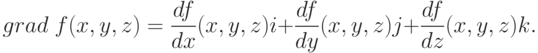
Здесь i, j, k - единичные векторы, параллельные координатным осям. Частные производные характеризуют изменение функции по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в окрестности точки (x, y, z). Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиента

определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке (x, y, z) меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются. Понятие градиента естественным образом переносится на функции любого числа переменных.

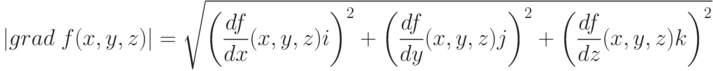
Перейдем к описанию метода градиентного спуска. Основная его идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея реализуется следующим образом.

Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции. Специальный выбор направления движения на каждом шаге позволяет надеяться на то, что в данном случае приближение к наименьшему значению функции будет более быстрым, чем в методе покоординатного спуска.

Метод требует вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно, заменяя их соответствующими разностными отношениями:

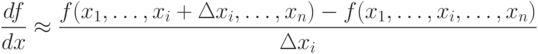
Отметим, что при таких расчетах 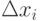, нельзя брать слишком малым, а значения функции нужно вычислять с достаточно высокой степенью точности, иначе при вычислении разности

будет допущена большая ошибка.

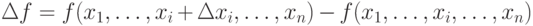
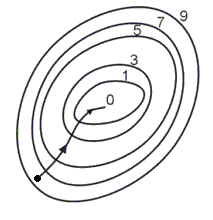
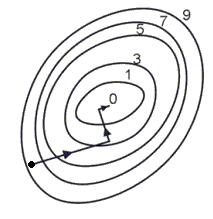
На рис.10.12 изображены линии уровня той же функции двух переменных u=f(x,y), что и на рис.10.11, и приведена траектория поиска ее минимума с помощью метода градиентного спуска. Сравнение рис.10.11 и рис.10.12 показывает, насколько более эффективным является метод градиентного спуска.