|
у меня аналогичная ситуация. Однако, если взять пример из приложения (ball_motion_04_click for trial.fla) то след остается. при этом заметил, что в моем проекте в поле "One item in library" виден кружок, в то время как в приложенном примере такого кружка нет. Вопрос знатокам, что не так? |
Рисование API
Функция рисования окружности
Теперь мы рассмотрим метод, который позволяет рисовать окружности с помощью API- рисования. Он более "хитрый". Многие методы рисования окружностей зависят от использования curveTo для формирования круга посредством рисования дуг. Этот же метод основан на принципе закругления концов линии. Если нарисовать линию, имеющую ширину в 100 пикселей, она может послужить основой для круга радиусом 100; функция Дэна рисует 0,15 пикселей от текущей точки рисования, что формирует прекрасный круг.
Параметры, передаваемые функции, являются координатами X и Y центра круга, а cWidth - ширина окружности.
function drawCircle(x, y, radius, cWidth) {
me = _root.createEmptyMovieClip("circle"+cnt,++cnt);
me.lineStyle(radius, 0x000000, 100);
me.moveTo(x, y);
me.lineTo(x, y+.15);
me.lineStyle(radius-cWidth, 0xffffff, 100);
me.moveTo(x, y);
me.lineTo(x, y+.15);
}
drawCircle(100, 100, 100, 20);В этом методе окружность расширена во внешнюю сторону от круга и включена в общий радиус. Мы также создаем фильм, в котором и рисуем круг.
Преобразуем эту функцию так, чтобы она работала как наши предыдущие функции, и затем добавим возможность указания цветов:
MovieClip.prototype.drawCircle = function (x, y, radius, cWidth) {
this.lineStyle(radius, 0x000000, 100);
this.moveTo(x, y);
this.lineTo(x, y+.15);
this.lineStyle(radius-cWidth, 0xffffff, 100);
this.moveTo(x, y);
this.lineTo(x, y+.15);
};
drawCircle(100, 100, 100, 20);Теперь добавим цвета:
MovieClip.prototype.drawCircle = function(x, y, radius,
КcWidth, innerCol, outerCol) {
this.lineStyle(radius, outerCol, 100);
this.moveTo(x, y);
this.lineTo(x, y+.15);
this.lineStyle(radius-cWidth, innerCol, 100);
this.moveTo(x, y);
this.lineTo(x, y+.15);
};
drawCircle(100, 100, 100, 10, 0xff0000, 0x000000);Здесь можно поэкспериментировать с порядком параметров, указав в первую очередь цвет заливки и радиус, а потом уже ширину окружности и ее цвет. Вы также можете изменить функцию так, чтобы можно было изменять цвет заполнения и рамки. Тогда можно нарисовать окружность без заливки.
Рисование кривой через указываемую точку
Мы настроили работу функции curveTo, указали начальную точку, конечную точку и точку управления. Но иногда полезнее проводить кривую через указываемую точку, поэтому мы создадим функцию для достижения этого результата.
Функция curveTo во Flash создает то, что называется квадратным уравнением для кривой Безье. Раньше кривые линии рисовали, проставляя серию точек на кривой, а затем воспризводя линии фильмов между этими точками, что достигалось с помощью уравнения кривой Безье.
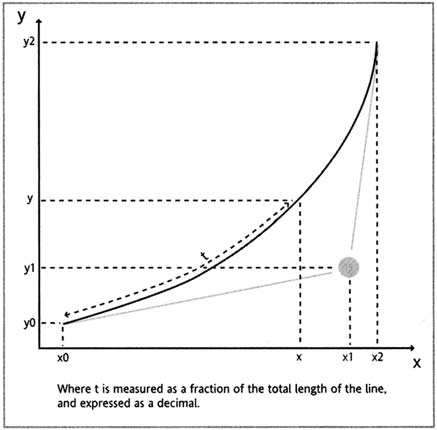
С помощью этого уравнения указывается конечная точка, точка контроля и начальная точка. Переменной в этом уравнении является t, которая изменяет значения от 0 до 1 от начала кривой и до ее конца. Мы можем вставлять различные значения t для выяснения координат любой отдельной точки на кривой.
Квадрат Безье
| x | Положение по оси X, через которое проходит кривая за в t |
| x0 | Начальная точка кривой по оси X |
| x1 | Контрольная точка прохождения кривой по оси X |
| X2 | Конечная точка кривой по оси X |
| y | Положение по оси Y, через которое проходит кривая в t |
| Y0 | Начальная точка кривой по оси Y |
| Y1 | Контрольная точка прохождения кривой по оси Y |
| Y2 | Конечная точка кривой по оси Y |
| t | Время |
Приведем наше уравнение.
x = x0*t*t + x1*2*t*(1-t) + x2*(1-t)*(1-t) y = y0*t*t + y1*2*t*(1-t) + y2*(1-t)*(1-t)
Это уравнение полезно для поиска отдельной точки, через которую проходит кривая, в любой точке t, от 0 до 1, т.е. от начала и до конца кривой. Мы указываем точку начала, точку контроля, конечную точку и t для перехода к позиции (X, Y) (в которой кривая проходит через эту точку).
Нам нужно изменить функцию таким образом, чтобы можно было указывать значения для точки начала (x0,y0), конца (x2,y2) и отдельной точки кривой (X, Y) и перейти в нужную точку контроля (x1,y1). Другими словами, нужно переработать функцию так, чтобы она выглядела примерно следующим образом.
x1= умноженное на x0, x2, x и t y1= умноженное на y0, y2, y и t
Это разумное упрощение. Мы рассмотрим его для уравнения для X и затем продублируем наши результаты для Y, так как уравнения идентичны. Прежде всего, нам нужно получить значения x1 и y1 в левой части уравнения. Это мы сделаем взаимным уничтожением с обеих сторон:
x - x1*2*t*(1-t) = x0*t*t + x1*2*t*(1-t) + x2*(1-t)*(1-t) - x1*2*t*(1-t)
Значения плюс и минус x1*2*t*(1-t) в правой части взаимно компенсируют друг друга:
x - x1*2*t*(1-t) = x0*t*t + x1*2*t*(1-t) + x2*(1-t)*(1-t) х1*2*t(1-t) x - x1*2*t*(1-t) = x0*t*t + x2*(1-t)*(1-t)
Теперь вычтем x из обеих сторон:
x - x1*2*t*(1-t) - x = x0*t*t + x2*(1-t)*(1-t) - x x - x1*2*t*(1-t) -x = x0*t*t + x2*(1-t)*(1-t) - x -x1*2*t*(1-t) = x0*t*t + X2*(1-t)*(1-t) - x -1*x1*2*t*(1-t) = x0*t*t + x2*(1-t)*(1-t) - x
Умножим -1 на 2 в левой части уравнения:
x1* - 2*t*(1-t) = x0*t*t + x2*(1-t)*(1-t) - x
Далее, делим обе части уравнения на (-2*t*(1-t) ):
x1*(-2*t*(1-t)) / (-2*t*(1-t)) = =(x0*t*t + x2*(1-t)*(1-t) - x) / (-2*t*(1-t))
С левой стороны имеем (-2*t*(1-t)) / (-2*t*(1-t)), что дает 1, поэтому можно произвести сокращение:
x1 (- 2 * t * (1 - t)) / ( - 2 * t * (1 - t) ) = =(x0*t*t + x2*(1-t)*(1-t) - x) / (-2*t*(1-t)) x1 = (x0*t*t + x2*(1-t)*(1-t)-x) / (-2*t*(1-t))
Мы получили уравнение для нахождения x1, а уравнением для y1 будет следующее:
y1 = (y0*t*t + y2*(1-t)*(1-t) - y) / (-2*t*(1-t))
Теперь можно использовать полученные результаты для создания функции, которая будет передавать значения x, y, x0, y0, x2, y2 и t для рисования кривой из (x0,y0) в (x2,y2), проходящей через точку (x,y) в точке на прямой, указываемой t.
Истинная роль t станет вам понятнее, когда вы начнете вставлять числа, которые будут влиять на форму кривой. Переименуем значения на a, b и c в нашей функции, для простоты. Мы будем вызывать функцию aToBThroughC чтобы выяснить значение каждой из величин. Приведем уравнение с добавленными a, b и c:
controlX = (ax*t*t + bx*(1-t)*(1-t) - cx) / (-2*t*(1-t)) controlY = (ay*t*t + by*(1-t)*(1-t) - cy) / (-2*t*(1-t))
Теперь перейдем к самой функции. Для простоты предположим, что мы настроили lineStyle.
MovieClip.prototype.aToBThroughC =
function (ax, ay, bx, by, ex, cy,t) {
var controlX = (ax*t*t+bx*(1-t)*(1-t)-cx)/(-2*t*(1-t));
var controlY = (ay*t*t+by*(1-t)*(1-t)-cy)/(-2*t*(1-t));
this.moveTo(ax, ay);
// for security
this.curveTo(controlx, controly, bx, by);
};Для проверки работы введите следующий код.
this.lineStyle (27, 0xff0000); this.aToBThroughC (100, 100, 250, 100, 200, 350, 0.5);
Сохраните ваш файл под именем AtoBthroughC.fla и запустите его. Мы создали сильно изогнутую кривую
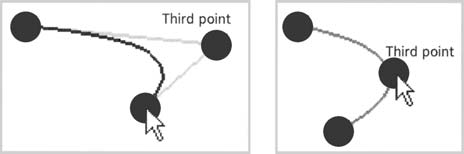
Чтобы показать корректность работы нашей функции, мы откроем созданный нами ранее файл curve with anchor.fla, и изменим его так, чтобы третья, перетаскиваемая, точка была точкой, через которую проходит кривая, а не точкой контроля. Измененный код выделен жирным шрифтом:
_quality = "LOW";
MovieClip. prototype. aToBThroughC = function (ax, ay, bx, by, ex, cy, t) {
var controlX = (ax*t*t+bx*(1-t)*(1-t)-cx)/(-2*t*(1-t));
var controlY = (ay*t*t+by*(1-t)*(1-t)-cy)/(-2*t*(1-t));
this.moveTo(ax, ay);
// for security
this.curveTo(controlx, controly, bx, by);
};
initObj = {onPress:dragOn, onRelease:dragOff,onReleaseOutside:dragOff,
КuseHandCursor: false};
this.attachMovie("point", "start_mc", 1, initObj);
this.attachMovie("point", "end_mc" , 2, initObj);
this.attachMovie("point", "control_mc", 3, initObj);
function dragOn() {
this.onMouseMove = dragMe;
}
function dragOff() {
delete this.onMouseMove;
}
function dragMe() {
this._x = _root._xmouse;
this._y = _root ._ymouse;
this._parent.reDraw();
}
function reDraw() {
this.clear();
this.lineStyle(2, 0xFF5555, 100);
this.aToBThroughC(start_mc._x, start_mc._y, end_mc._x, end_mc._y,
Кcontrol_mc._x, control_mc._y, 0.5);
}
Пример
3.1.
Вы увидите, что при перетаскивании точек кривая теперь всегда проходит через третью точку.
Задав другое значение t, вы увидите, что кривая изменила форму.
this.aToBThroughC(start_mc._x, start_mc._y, end_mc._x, end_mc._y, Кcontrol_mc._x, control_mc._y, 0.1); }
Переменная t может иметь любое значение между 0 и 1, поэтому здесь может быть огромное количество кривых, которые будут проходить через нашу точку c - по одной для каждого значения между 0 и 1.