Оптимизация производственных моделей

Задача 2.2. Раскрой листовых материалов

Механическому цеху требуется из куска листового металла выкроить развертку для изготовления короба. Короб можно изготовить так: сделать по углам квадратные вырезы, отогнуть боковины и соединить боковые швы сваркой. Можно ли из имеющихся в цехе стандартных листов размером 1,0 м х 2,0 м изготовить коробы объемом 200 л? Составить математическую модель. Формализовать задачу в MS Excel для других размеров листов при условии максимальной вместимости короба. Поставщики выпускают стальной лист следующего сортамента (м): 1х2, 1х3, 2х2, 2х2,5, 2х3. Построить графики зависимости максимальной вместимости (куб. м) и остатков материала (кв. м) от площади квадратных листов (кв. м).

Решение задачи

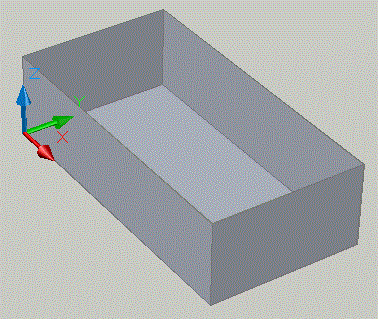
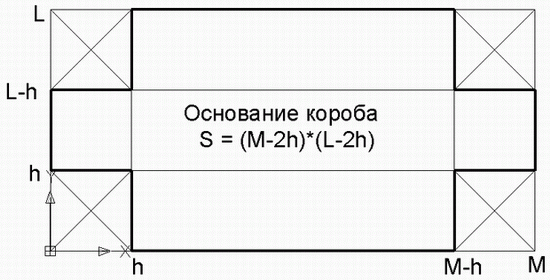
1. Составим ментальной карту в виде выкройки и эскиза готовой конструкции, представленных на рисунке 2.10.
   

   
   
   

   
   Рис. 2.10. Раскрой листа для изготовления короба
2. Составим математическую модель в виде формулы для объема короба.

   Площадь листа:

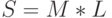
   Объем короба равен произведению площади основания на высоту:

   Остатки материала:
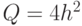
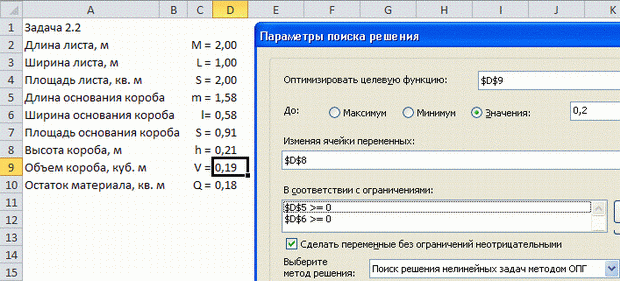
3. Сформируем таблицу в MS Excel (справа показана вставка формул в ячейки столбца D). В ячейку D8 помещаем искомую переменную — высоту короба . Вписываем в ячейку произвольное число, например, 0,10 м. Целевая функция помещена в ячейку D9 — это объем короба.
   

   
   
4. В параметрах поиска решения устанавливаем требуемое значение целевой функции . В ограничениях указываем, что длина и ширина основания короба должны быть положительными числами. Данная задача нелинейная: Объем короба и площадь остатков нелинейно зависят от высоты короба.
   

   
   увеличить изображение
   
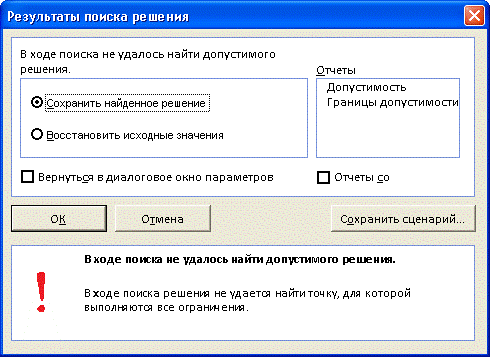
   В результате поиска программа выдает отрицательный результат:
   

   
   

   Программа нашла, что при высоте короба 21 см его вместимость будет составлять только 192,45 л, — из имеющегося материала изготовить короб объемом 200 л невозможно.

   Проверим теперь, что этот объем есть максимально возможный. В параметрах поиска решения предложим оптимизировать целевую функцию до максимума. Программа подтвердит, что объем 192,45 л есть максимально возможный.

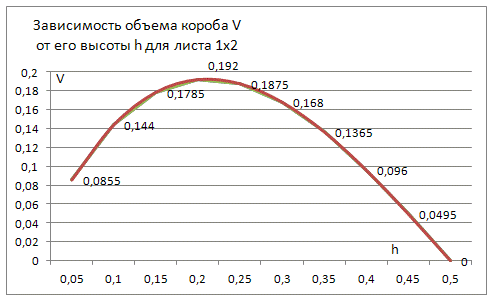
   Для иллюстрации построим зависимость объема короба от его высоты по формуле

   (рисунок 2.11)

   

   
   Рис. 2.11. Нелинейная зависимость объема короба от его высоты
5. Проведем требуемый анализ максимальной вместимости короба для других размеров листов со сторонами м) 1х3, 2х2, 2х2,5, 2х3. Для этого продолжим таблицу, указывая другие размеры листов. Устанавливаем целевые ячейки в строке 9. Далее вызываем программу "Поиск решения" для каждого варианта и ищем максимальное значение целевой функции. Построим графики максимальной вместимости короба и остатков материала при раскрое в зависимости от площади листа:
   

   
   
6. Выводы:

   Максимальная вместимость короба почти линейно возрастает с увеличением площади листа заготовки. При этом около 10% листа уходит в отходы.