Алгоритмы повышения количества оттенков (псевдотонирования)

11.4. Алгоритм рассеивания ошибок Флойда-Стейнберга

Данный метод также является модификацией алгоритма усечения по порогу, рассмотренного в разделе "Алгоритмы повышения количества оттенков (псевдотонирования)" . Идея состоит в распределении (рассеивании) ошибки, возникшей при аппроксимации данного пикселя, на соседние пиксели. Существуют разные варианты распределения ошибки на соседние пиксели. Приведем тот вариант, который использует все доступные (при однопроходном построчном алгоритме) непосредственные соседние пиксели в 8-связном смысле и является оптимальным [30]. 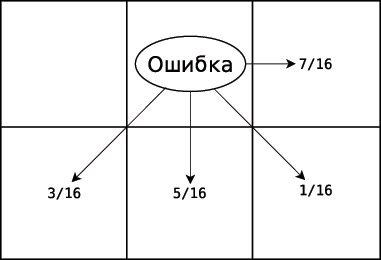Осуществляется проход изображения сверху вниз, слева направо и применяется усечение по порогу; при этом ошибка распределяется следующим образом (см. рис. 11.6): к значению атрибута пикселя справа добавляется ошибки, справа внизу добавляется ошибки, внизу добавляется ошибки, слева внизу добавляется ошибки.

Рис. 11.6. Распределение ошибки.

// проход по пикселям строго справа налево, сверху вниз
// Threshold - порог, I(pixel) - атрибут пикселя
// pixel.right - пиксель справа, pixel.down - пиксель внизу
// pixel.down_right - пиксель справа внизу
// pixel.down_left - пиксель слева внизу
foreach( pixel in 8bit_picture ) //для каждого пикселя
{
      if( I(pixel) > Threshold )
      {
          I(pixel) = Белый;
          Error = I(pixel) - Белый;
      }
      else
      {
          I(pixel) = Черный;
          Error = I(pixel) - Черный;
      }
      I(pixel.right)+= 7/16 * Error;
      I(pixel.down_right)+= 1/16 * Error;
      I(pixel.down)+= 5/16 * Error;
      I(pixel.down_left)+= 3/16 * Error;
}

Важно отметить, что для предотвращения возникновения артефактов в изображении сумма четырех частей ошибки должна быть в точности равна ошибке. При этом не допускается округлений. Этого можно добиться путем вычисления последней составляющей ошибки как разности ошибки и первых трех составляющих.

Пример работы алгоритма можно видеть на рис. 11.7. Видно, что метод сохраняет мелкие детали, в отличие от описанного в разделе "Алгоритмы повышения количества оттенков (псевдотонирования)" . По сравнению с методом из раздела 11.3, также видны улучшения - эффект периодичности практически исчез. Однако этот алгоритм является самым медленным из всех описанных в данной лекции.

Рис. 11.7. Результат работы алгоритма рассеивания ошибок.