Алгоритмы повышения количества оттенков (псевдотонирования)
11.3. Алгоритм упорядоченного размытия
Очевидно, что метод, рассмотренный в "Алгоритмы повышения количества оттенков (псевдотонирования)" , требует улучшений. Можно специально добавить в исходное изображение шум1некоторую, часто случайную, величину , а затем применить алгоритм 11.1. Если добавлять произвольный шум, то результаты алгоритма нельзя считать удовлетворительными.
Тем не менее существует искусственный псевдошум, который минимизирует эффект периодичности, т.е. появления на изображении некоторого упорядоченного узора. Данный шум возможно задать с помощью квадратной матрицы специального вида [13]. Такая матрица называется матрицей размытия2(англ.) dither matrix. Сначала исходное изображение разбивается на квадратные области размером NxN, совпадающие с размерностью матрицы размытия, затем к каждому квадрату применяется алгоритм 11.2, где в качестве порога выбирается соответствующее значение из матрицы.
Для случая 2x2 оптимальной является следующая матрица:
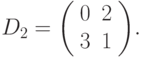
Для получения матриц большего размера следует использовать следующие рекурсивные соотношения:
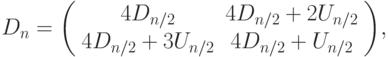
где
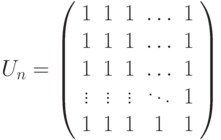
- матрица, состоящая из единиц размером nxn. Например, матрица размером 4x4 будет следующая:
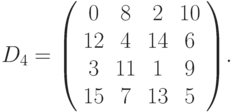
Матрица размытия Dn позволяет получить n2 значений атрибутов; при этом пространственное разрешение не изменяется. Ниже приведен псевдокод алгоритма:
foreach( pixel in 8bit_picture ) // для каждого пикселя
{
// I(pixel) - атрибут пикселя
// Dn(i,j) - матрица размытия, n - размер матрицы
// X Mod Y - остаток от деления X на Y
// i, pixel.Y - координаты строк
i = pixel.Y Mod n;
// j, pixel.X - координаты столбцов
j = pixel.X Mod n;
if( I(pixel) > Dn(i,j) )
I(pixel) = Белый;
else
I(pixel) = Черный;
}
Листинг
11.2.
Алгоритм псевдотонирования - упорядоченное размытие
Как видно из рис. 11.5 результаты работы данного алгоритма намного лучше, чем описанного в разделе "Алгоритмы повышения количества оттенков (псевдотонирования)" , - изображение выглядит более детально.



